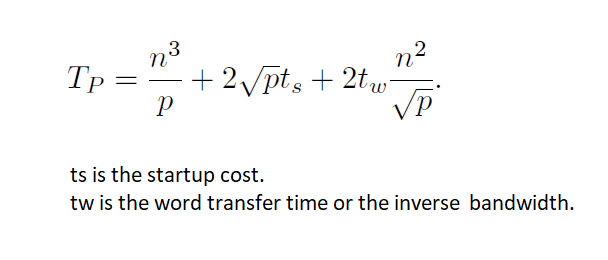Cannon’s algorithm for distributed matrix multiplication

Cannon's algorithm is a distributed algorithm for matrix multiplication for two-dimensional meshes. It is especially suitable for computers laid out in an N × N mesh. While Cannon's algorithm works well in homogeneous 2D grids, extending it to heterogeneous 2D grids has been shown to be difficult.

The main advantage of the algorithm is that its storage requirements remain constant and are independent of the number of processors.

Cannon’s algorithm

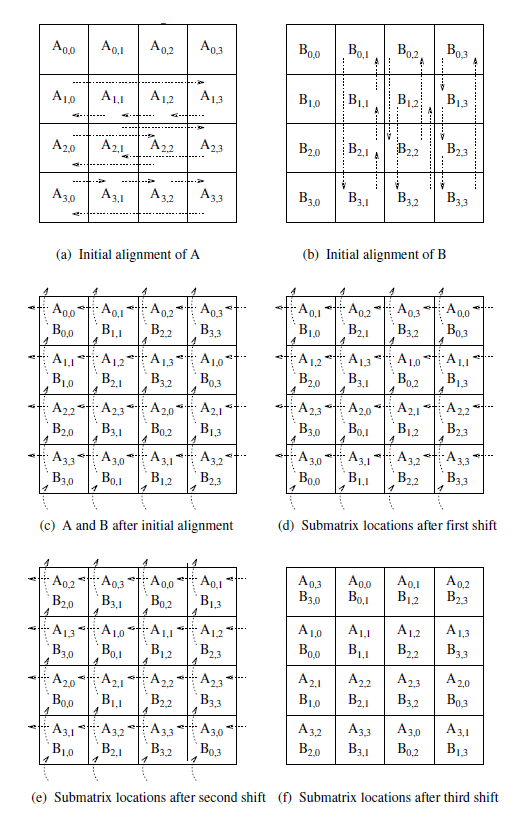
1. Consider two n × n matrices A and B partitioned into p blocks.

2. A(i , j) and B(i , j) (0 ≤ i,j ≤ √p ) of size (n ∕ √p)×(n ∕ √p) each.

3. Process P(i , j) initially stores A(i , j) and B(i , j) computes block C(i , j) of the result matrix.

4. The initial step of the algorithm regards the alignment of the matrixes.

5. Align the blocks of A and B in such a way that each process can independently start multiplying its local submatrices.

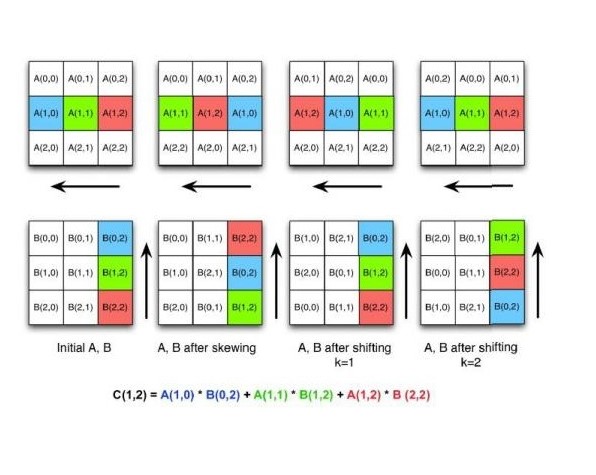
6. This is done by shifting all submatrices A(i , j) to the left (with wraparound) by i steps and all submatrices B(i , j) up (with wraparound) by j steps.

7. Perform local block multiplication.

8. Each block of A moves one step left and each block of B moves one step up (again with wraparound).

9. Perform next block multiplication, add to partial result, repeat until all blocks have been multiplied.

   

Scaling and Distributing the Subtasks among the Processors:

1. The sizes of the matrices blocks can be selected so that the number of subtasks will coincides the number of available processors p,
2. The most efficient execution of the parallel Canon’s algorithm can be provided when the communication network topology is a two-dimensional grid,
3. In this case the subtasks can be distributed among the processors in a natural way:the subtask (i,j) has to be placed to the p(i,j) processor.

Pseudocode

* forall i=0 to √p -1
       CShift-left A [i; :] by i 
* forall j=0 to √p -1
       Cshift-up B[: , j] by j 
* for k=0 to √p -1
       forall i=0 to √p -1 and j=0 to √p -1
           C[i,j] += A[i,j] * B[i,j] 
           CShift-leftA[i; :] by 1 
           Cshift-up B[: , j] by 1 
       end forall
 end for

Example:
Let A and B be two dimenstional square matrices of size 3*3.

Complexity

1. In the initial alignment step, the maximum distance over which block shifts is √? −1

2. The circular shift operations in row and column directions take time:?????=2(ts+twn²∕p)

3. Each of the √? single-step shifts in the compute-and-shift phase takestime:ts+twn²∕p

4. Multiplying √? submatrices of size (n/√?)×(n/√?) takes time: n³/?.

5. Parallel time:

   

6. The isoefficiency function of Cannon's algorithm is O(p^3/2).

Implementations

• C

    #include <stdio.h>
    #include <stdlib.h>
    #include <math.h>
    #include <mpi.h>
    #define N 16384
    int main(int argc, char *argv[])
    {
    MPI_Comm cannon_comm;
    MPI_Status status;
    int rank,size;
    int shift;
    int i,j,k;
    int dims[2];
    int periods[2];
    int left,right,up,down;
    double *A,*B,*C;
    double *buf,*tmp;
    double start,end;
    unsigned int iseed=0;
    int Nl,N;
    printf("Matrix size:");
    printf("\n");
    scanf("%d", &N);
    MPI_Init(&argc,&argv);
    MPI_Comm_rank(MPI_COMM_WORLD,&rank);
    MPI_Comm_size(MPI_COMM_WORLD,&size);
    srand(iseed);
    dims[0]=0; dims[1]=0;
    periods[0]=1; periods[1]=1;
    MPI_Dims_create(size,2,dims);
    if(dims[0]!=dims[1]) {
    if(rank==0) printf("The number of processors must be a square.\n");
    MPI_Finalize();
    return 0;
    }
    Nl=N/dims[0];
    A=(double*)malloc(Nl*Nl*sizeof(double));
    B=(double*)malloc(Nl*Nl*sizeof(double));
    buf=(double*)malloc(Nl*Nl*sizeof(double));
    C=(double*)calloc(Nl*Nl,sizeof(double));
    for(i=0;i<Nl;i++)
    for(j=0;j<Nl;j++) {
    A[i*Nl+j]=5-(int)( 10.0 * rand() / ( RAND_MAX + 1.0 ) );
    B[i*Nl+j]=5-(int)( 10.0 * rand() / ( RAND_MAX + 1.0 ) );
    C[i*Nl+j]=0.0;
    }
    MPI_Cart_create(MPI_COMM_WORLD,2,dims,periods,1,&cannon_comm);
    MPI_Cart_shift(cannon_comm,0,1,&left,&right);
    MPI_Cart_shift(cannon_comm,1,1,&up,&down);
    start=MPI_Wtime();
    for(shift=0;shift<dims[0];shift++) {
    // Matrix multiplication
    for(i=0;i<Nl;i++)
    for(k=0;k<Nl;k++)
    for(j=0;j<Nl;j++)
    C[i*Nl+j]+=A[i*Nl+k]*B[k*Nl+j];
    if(shift==dims[0]-1) break;
    // Communication
    MPI_Sendrecv(A,Nl*Nl,MPI_DOUBLE,left,1,buf,Nl*Nl,MPI_DOUBLE,right,1,cannon_comm,&status);
    tmp=buf; buf=A; A=tmp;
    MPI_Sendrecv(B,Nl*Nl,MPI_DOUBLE,up,2,buf,Nl*Nl,MPI_DOUBLE,down,2,cannon_comm,&status);
    tmp=buf; buf=B; B=tmp;
    }
    MPI_Barrier(cannon_comm);
    end=MPI_Wtime();
    if(rank==0) printf("Time: %.4fs\n",end-start);
    free(A); free(B); free(buf); free(C);
    MPI_Finalize();
    return 0;
    }