Double Ended Queue (Deque)

Reading time: 25 minutes | Coding time: 10 minutes

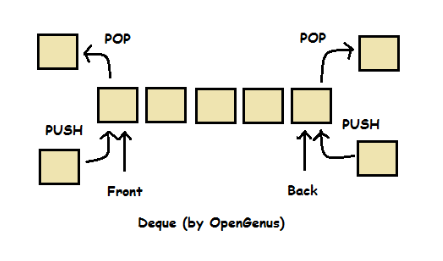
There are two variants of a double-ended queue. They include:

• Input restricted deque: In this dequeue,insertions can be done only at one of the ends,while deletions can be done from both ends.
• Output restricted deque: In this dequeue,deletions can be done only at one of the ends,while insertions can be done on both ends.

Pseudocode

There are four basic operations in usage of Deque that we will explore:

• Insertion at rear end
• Insertion at front end
• Deletion at front end
• Deletion at rear end

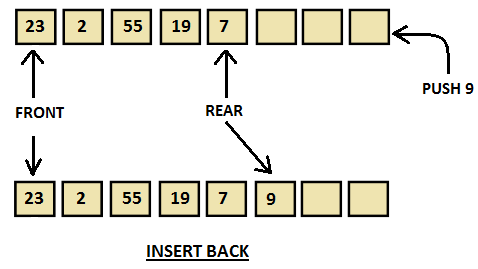
Algorithm for Insertion at rear end

Step-1: [Check for overflow]   
		if(rear==MAX)  
			Print("Queue is Overflow”);  
			return;  
Step-2:  [Insert Element]	  
		else  
			rear=rear+1;  
			q[rear]=no;      
		[Set rear and front pointer]                
		if rear=0  
			rear=1;  
		if front=0  
			front=1;  
Step-3: return

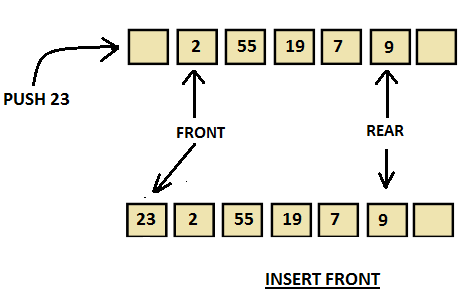
Algorithm for Insertion at front end

Step-1 :  [Check for the front position]  
		if(front<=1)  
			Print("Cannot add item at the front”);  
			return;  
Step-2 :  [Insert at front]  
		else  
			front=front-1;  
			q[front]=no;  
Step-3  : Return

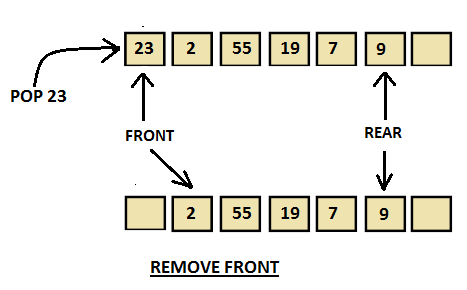
Algorithm for Deletion from front end

Step-1 [ Check for front pointer]  
		if front=0  
			print(" Queue is Underflow”);  
			return;  
Step-2 [Perform deletion]          
		else  
			no=q[front];  
			print(“Deleted element is”,no); 
		[Set front and rear pointer]       
		if front=rear  
			front=0;  
			rear=0;  
		else  
			front=front+1;  
Step-3 : Return

Algorithm for Deletion from rear end

Step-1 : [Check for the rear pointer]  
		if rear=0  
			print(“Cannot delete value at rear end”);  
			return;  
Step-2:  [ perform deletion]  
		else  
			no=q[rear];  
			[Check for the front and rear pointer]  
		if front= rear  
			front=0;  
			rear=0;  
		else  
			rear=rear-1;  
			print(“Deleted element is”,no);  
Step-3 : Return

Complexity

• Insertion or deletion in the middle is O(n)
• The time complexity of random access by index is O(1)
• time complexity of all enque(insert)/deque(delete) operations is O(1)

Implementations

#include <iostream>
using namespace std;
#define MAX 10 
int deque[MAX];
int leftt =-1 ;
int rightt = -1 ;
void inputdeque(void);
void outputdeque(void); 
void insertleft(void);
void insertright(void); 
void deleteleft(void); 
void deleteright(void); 
void display(void); 
int main( ) 
{ 
	int option; 
	cout<<"\n ----MAIN MENU----"; 
	cout<<"\n 1.Input restricted deque"; 
	cout<<"\n 2.Output restricted deque"; 
	cout<<"\n Enter your option : "; 
	cin>>option; 
	switch (option) 
	{  
		case 1:   inputdeque();   
			    	break;  
		case 2:   outputdeque();   
				break; 
	} return 0;
} 
void inputdeque( ) 
{ 
	int option;
	do 
	{  
		cout<<"\n\n INPUT RESTRICTED DEQUE";  
		cout<<"\n 1.Insert at right";  
		cout<<"\n 2.Delete from left";  
		cout<<"\n 3.Delete from right";  
		cout<<"\n 4.Display";  
		cout<<"\n 5.Quit";  
		cout<<"\n Enter your option : ";  
		cin>>option ;  
		switch (option)  
		{   
			case 1:    insertright();    
					break;   
			case 2:    deleteleft();    
					break;   
			case 3:    deleteright();    
					break;   
			case 4:    display();    
					break;  
		} 
	} while (option!=5);
} 
void outputdeque( ) 
{ 
	int option; 
	do 
	{  
		cout<<"\n\n OUTPUT RESTRICTED DEQUE";  
		cout<<"\n 1.Insert at right";  
		cout<<"\n 2.Insert at left";  
		cout<<"\n 3.Delete from left";  
		cout<<"\n 4.Display";  
		cout<<"\n 5.Quit";  
		cout<<"\n Enter your option : ";  
		cin>>option ;   
		switch(option)  
		{   
			case 1:    insertright();
			  	    	break;   
			case 2:    insertleft();    
					break;   
			case 3:    deleteleft(); 
			   		break;   
			case 4:    display();    
					break;  
		}
	}while (option!=5); 
} 
void insertright( ) 
{ 
	int val; 
	cout<<"\n Enter the value to be added:" ; 
	cin>>val; 
	if ( (leftt == 0 && rightt == MAX-1 ) || (leftt == rightt+1) )
	{  
		cout<<"\n OVERFLOW";
	    return; 
	}
	if (leftt == -1) 	// Queue is Empty Inititally
	{  
		leftt = 0;  
		rightt = 0;
    } 
	else 
	{
  		if (rightt == MAX-1) 	//right is at last position of queue    
			rightt = 0;
	  	else   
	  		rightt = rightt+1; 
	} 
	deque[rightt] = val ; 
} 
void insertleft( ) 
{ 
	 int val;
	 cout<<"\n Enter the value to be added:"; 
	 cin>>val; 
	if( (leftt ==0 && rightt == MAX-1) || (leftt == rightt+1) )
	{  
	 	cout<<"\n OVERFLOW";  
		return; 
	}
	if (leftt == -1)			//If queue is initially empty
	{  
		leftt = 0;  
		rightt = 0; 
	} 
	else 
	{  
		if(leftt == 0)
		    leftt = MAX - 1 ;  
		else   
		    leftt = leftt - 1 ; 
	} 
	deque[leftt] = val; 
}
void deleteleft( ) 
{ 
	if ( leftt == -1 ) 
	{  
		cout<<"\n UNDERFLOW";  
		return ; 
	}
	cout<<"\n The deleted element is : "<< deque[leftt];
	if (leftt == rightt) 										 
	{  
		leftt = -1 ;  
		rightt = -1 ; 
	} 
	else 
	{  
		if ( leftt == MAX - 1 )   
		    leftt = 0;  
		else   
		    leftt = leftt+1; 
	} 
} 	
void deleteright() 
{ 
	if ( leftt == -1 ) 
	{  
		cout<<"\n UNDERFLOW";
		return ; 
	} 
	cout<<"\n The element deleted is : "<< deque[rightt]; 
	if (leftt == rightt) 											
	{  	
		leftt = -1 ;  
		rightt = -1 ; 
	} 
	else 
	{  
		if (rightt == 0)   
			rightt = MAX - 1 ;  
		else   
			rightt = rightt - 1 ; 
	} 
} 
void display( ) 
{ 
	int front = leftt, rear = rightt;
	if ( front == -1 ) 
	{  
	 	cout<<"\n QUEUE IS EMPTY";  
		 return; 
	} 
	cout<<"\n The elements of the queue are : ";
	if (front <= rear ) 
	{  
		while (front <= rear)  
		{   
			cout << deque[front] <<" ";   
			front++;  
		} 
	} 
	else 
	{  
		while (front <= MAX - 1)  
		{   
			cout << deque[front] <<" ";   
			front++;  
		}  
		front = 0;  
		while (front <= rear)  
		{   
			cout<< deque[front]<<" ";   
			front++;  
		} 
	} 
	cout<<endl;
}

Applications

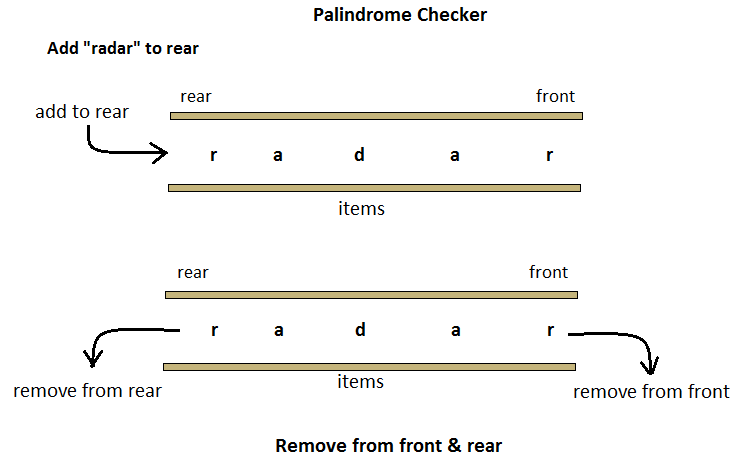
• Palindrome Checker

• A-Steal job scheduling algorithm
• The A-Steal algorithm implements task scheduling for several
  processors(multiprocessor scheduling).
  • The processor gets the first element from the deque.
  • When one of the processor completes execution of its own
    threads it can steal a thread from another processor.
  • It gets the last element from the deque of another processor
    and executes it.
• Undo-Redo operations in Software applications.