The exclusive book “Binary Tree Problems” (by OpenGenus) is carefully crafted to present you the knowledge and practice (around the data structure, Binary Tree) needed to ace Coding Interviews and Competitive Coding Contests.

Go through this complete article to get the complete idea why you need this book.

Background

In 2015, Max Howell, the creator of Homebrew was interviewed and rejected by Google. He ranted about this on Twitter as he was not able to invert a Binary Tree (can you?). Everyone at Google uses his software, Homebrew but he could not manage to get hired.

Homebrew is a package manager which helps manage installation of software on MacOS and Linux operating systems. It was developed by Max in 2009.

This is the tweet by Max Howell:

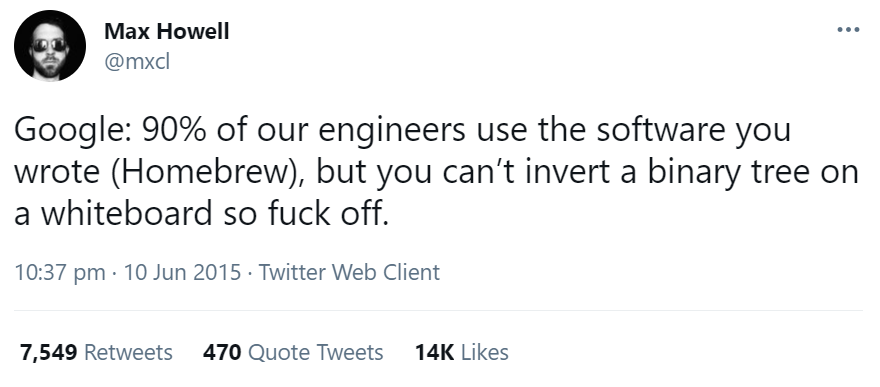
The frustration is real but it is a tough problem if you are not in rigorous practice. You need not worry now as we, at OpenGenus, have developed a book exclusively to master Binary Tree problems.

In fact, Binary Tree remains the most common domain from which questions are asked at Software Developer Interviews at top companies like Google, Facebook, Amazon, Microsoft, Apple and others.

Get this book

Get this Book now:

• Amazon.in: amazon.in/dp/B094YJ1K13
• Amazon.com: amazon.com/dp/B094YJ1K13

See a glimpse of our book (Page 136 and 137):

See the complete preview at Amazon.

More about the Book

The book takes you through the fundamentals of Binary Tree, presents how to implement it in a good and secure way, make you practice key problems, present variants like Threaded Binary Tree, Binary Space Partitioning Tree, Skewed Binary Tree, AVL Tree, Treap and much more.

The content covered is deep and is not covered by any other standard book.

Each chapter is followed by a brief note of insight which wraps up your though in the correct direction and is a feast for budding Independent Researchers.
If you aspire you to a good Software Developer, you should definitely get this book. You will be prepared to apply Binary Tree is designing solutions to key real life problems like designing an Excel sheet or making Game Graphics render fast.

The content in the Book is carefully designed. The chapters in this book are:

1. About this book
2. Binary Tree
3. Properties of Binary Tree
4. Implementation of Binary Tree
5. Implementation of Binary Tree with no NULL

Do you know why we need to avoid NULL? and how we can do this? Following this, enables you to write production ready code and is an INSTANT YES signal at Coding Interviews.

6. Intuitive View of a Binary Tree

This is important as it will enable you to imagine problems and solve it instantly without any pen and paper.

7. Traversing a Binary Tree (Preorder, Postorder, Inorder)
8. Convert Inorder+Preorder to Binary Tree (+ other combinations)

These above 2 topics are fundamental and many get these wrong. You must get this right.

9. Find height or depth of a binary tree
10. Find Level of each node from root node
11. Diameter of a Binary Tree
12. Finding Diameter of a Tree using DFS
13. Check if a Binary Tree is Balanced by Height
14. Find number of Universal Value subtrees in a Binary Tree
15. Counting subtrees where nodes sum to a specific value
16. Find if a given Binary Tree is a Sub-Tree of another Binary Tree
17. Check if a Binary Tree has duplicate values
18. Find nodes which are at a distance k from root in a Binary Tree
19. Finding nodes at distance K from a given node
20. Find ancestors of a given node in a binary tree
21. Largest Independent Set in Binary Tree
22. Copy a binary tree where each node has a random pointer
23. Serialization and Deserialization of Binary Tree
24. 0-1 Encoding of Binary Tree
25. ZigZag Traversal of Binary Tree
26. Check if 2 Binary Trees are isomorphic
27. Convert Binary Tree to Circular Doubly Linked list

In this, we cover a variant that is Skewed Binary Tree. This helps us work with an extreme version.

28. Introduction to Skewed Binary Tree
29. Check if Binary Tree is skewed or not
30. Change Binary Tree to Skewed Binary Tree

In this, we cover a variant that is Threaded Binary Tree.

31. Threaded Binary Tree
32. Operations in Threaded Binary Tree
33. Convert Binary Tree to Threaded Binary Tree

In this, we cover a variant that is Binary Search Tree. This helps us work with the most optimal version for most problems.

34. Binary Search Tree
35. Converting a Sorted Array to Binary Tree
36. Minimum number of swaps to convert a binary tree to binary search tree
37. Find minimum or maximum element in Binary Search Tree
38. Convert Binary Search Tree to Balanced Binary Search Tree
39. Find k-th smallest element in Binary Search Tree
40. Sum of k smallest elements in Binary Search Tree

The remaining chapters who advanced variants of Binary Tree which helps you to fine tune your skills and write optimal code.

41. Different Self Balancing Binary Trees
42. AVL Tree
43. Splay Tree
44. Binary Space Partitioning Tree
45. Binary Heap
46. Treap
47. Some real problems
48. Applications & Concluding Note

With this, you have all knowledge to easily Invert a Binary Tree.

Go ace your upcoming Interview now. Best of Luck.

---

About the Authors and Contributors:

Authors: Aditya Chatterjee; Srishti Guleria; Ue Kiao;

• Aditya Chatterjee is an Independent Researcher and the Founding Member of OPENGENUS, a scientific community focused on Computing Technology.
• Srishti Guleria is a Maintainer and Software Developer, Intern at OpenGenus specializing in Tree Data Structures. She is a Computer Science student at Rajasthan Technical University, Kota.
• Ue Kiao is a Japanese Software Developer and has played key role in designing systems like TaoBao, AliPay and many more. She has completed her B. Sc in Mathematics and Computing Science at National Taiwan University and PhD at Tokyo Institute of Technology.

Contributors (16): Benjamin QoChuk, Hrithik Shrivastava, Parth Maniyar, Priyanshi Sharma, Rohit Topi, Amruta U. Koshe, Ayush Sonare, Akshay Gopani, Rashmitha, Manasvi Singh, Sahil Silare, Vaibhav Gupta, Vishnu S Reddy, Kyatham Srikanth, Rupali Kavale, Yash Aggarwal;