Binary Search Tree (BST) in Python using OOP concepts

In this article at OpenGenus, we will be implementing Binary Search Tree in Python using OOPs concepts.

Table of Contents

1. About binary search tree
2. Example
3. Implementation in Python
4. Time Complexity
5. Space Complexity

What is a Binary Search Tree

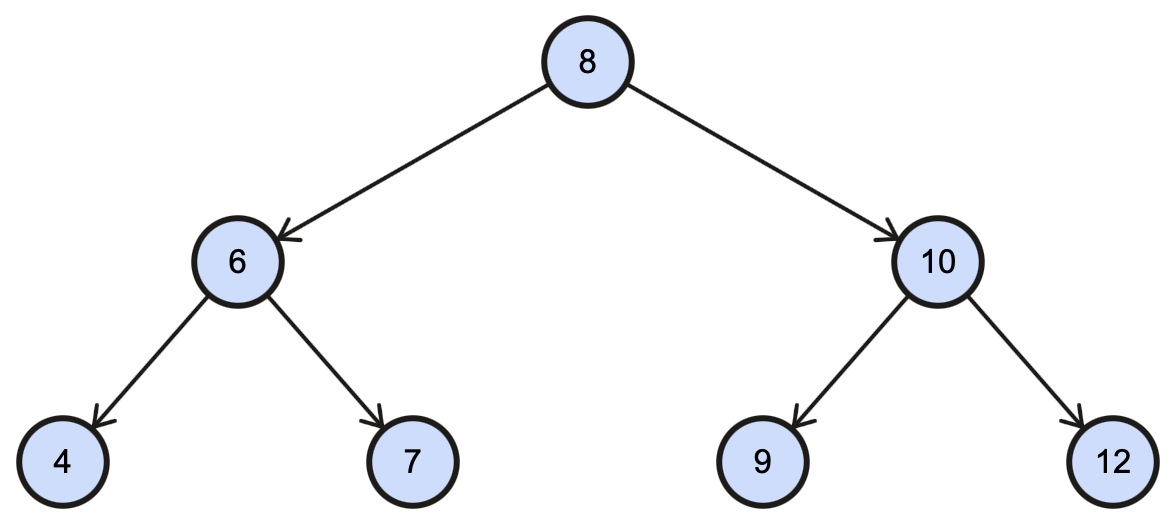
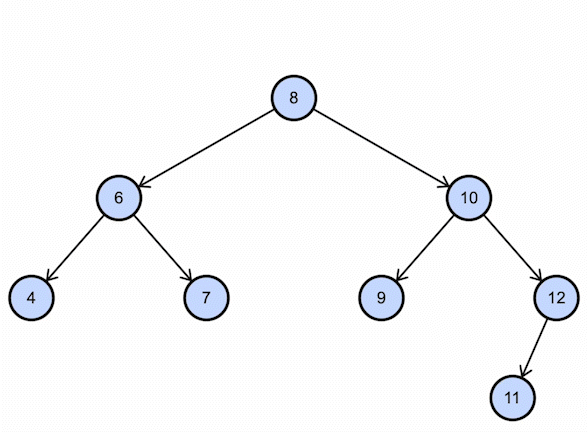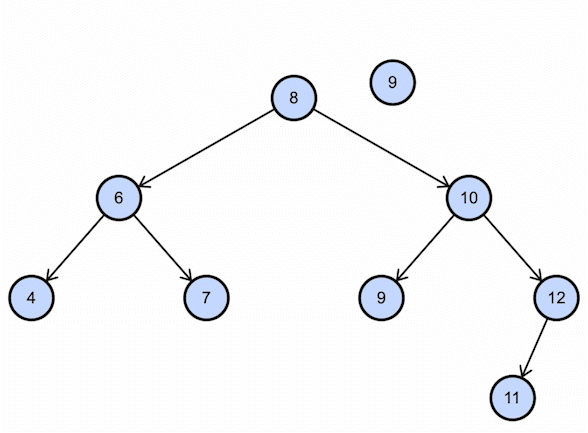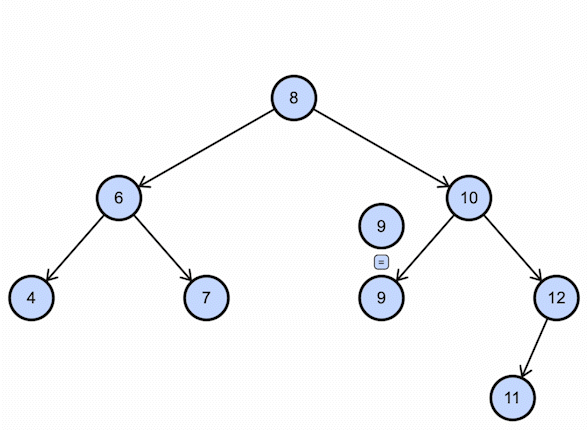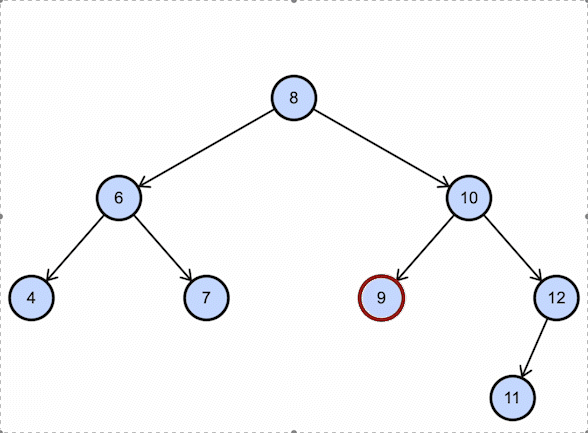
Binary Search Tree or BST is a tree in which all the nodes in the left subtree have a value less than the root node and every node in the right subtree has a value greater than the root node.

For example:-

Implementing BST in Python using OOPs concepts

Let's begin implementing Binary Search Tree using OOP concepts in Python.

Before creating the BST class, we know that Binary Search Tree will contain nodes, so let us first create a class for them.
Let's name this class as BSTNode. It will have three variables, left to store the left child, right to store the right child and val to store the value of that node.

class BSTNode:
    def __init__(self, val):
        self.left = None
        self.right = None
        self.val = val

Since we have created a node class for BST, now let's create the BST class.
Our BST class will contain a root pointer pointing to the root node, such that when the constructor is called, it will assign root to None.

class BST:
    def __init__(self):
        self.root = None

We will be implementing three operations in this tutorial:-

1. Insert in BST
2. Search in BST
3. Delete in BST

Insert value in Binary Search Tree (BST)

We will create an insert() method that will insert a new node with the given value in the binary search tree.

If the tree is empty, it will create a new node and set it as the root node. Otherwise, it will call the _insert() method to recursively insert the new node into the correct position.

    def insert(self, val):
        if self.root is None:
            self.root = BSTNode(val)
        else:
            self._insert(val, self.root)

    def _insert(self, val, node):
        if val < node.val:
            if node.left is None:
                node.left = BSTNode(val)
            else:
                self._insert(val, node.left)
        elif val > node.val:
            if node.right is None:
                node.right = BSTNode(val)
            else:
                self._insert(val, node.right)

The _insert() method recursively traverses the tree until it finds the correct position for the new node. If the value is less than the current node's value, it goes to the left subtree. Otherwise, it goes to the right subtree. If the appropriate child node is None, it creates a new node with the given value and sets it as the child node. Otherwise, it continues recursively traversing the subtree.

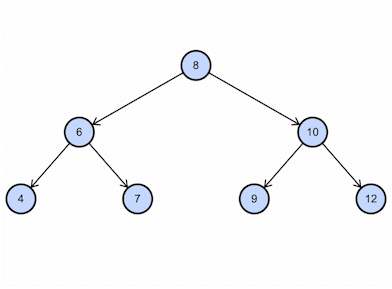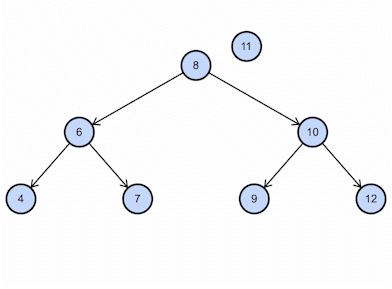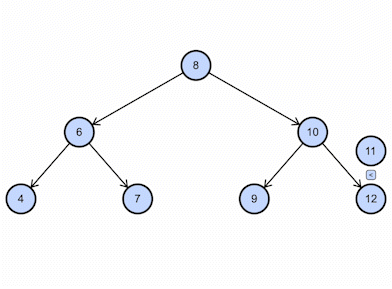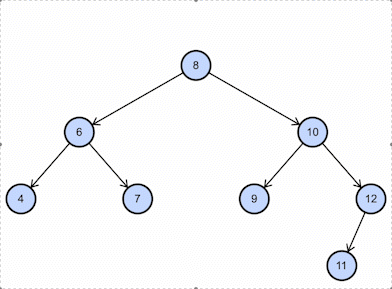
Consider the BST example shown above; if we want to insert 11, this is how it will work:

Search for a given value in Binary Search Tree (BST)

For searching a given value in our binary search tree, we will create a search() function which will call _search() method to recursively search for the node starting from the root node.

The _search() method recursively traverses the tree, comparing the value with the current node's value. If the current node is None, it returns False. If the current node's value is equal to the given value, it will return True. If the value is less than the current node's value, it continues searching in the left subtree; otherwise in the right subtree.

    def search(self, val):
        return self._search(val, self.root)

    def _search(self, val, node):
        if node is None:
            return False
        elif node.val == val:
            return True
        elif val > node.val:
            return self._search(val, node.right)
        else:
            return self._search(val, node.left)

Consider the BST example shown above; if we want to find 9, this is how it will work:

Deleting the value in Binary Search Tree (BST)

The Delete function is used to remove the given node from a binary search tree. This function is also recursive, but it has an additional feature where it returns the updated state of the given node after performing the delete operation. This ensures that a parent node whose child has been deleted can correctly update its left or right data member by setting it to None. But we have to delete a node from a binary search tree in a way that doesn't break any of its properties. Removing a node from a binary search tree can happen in three different scenarios:-

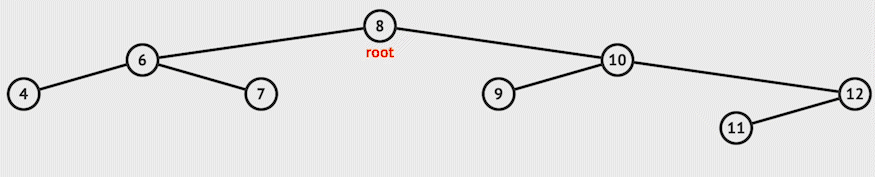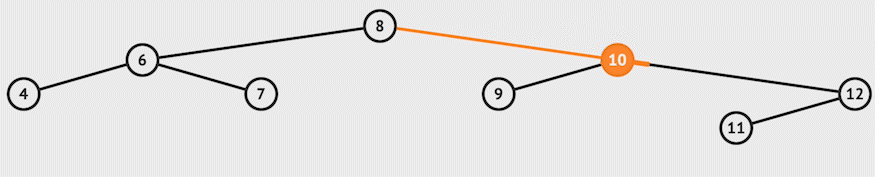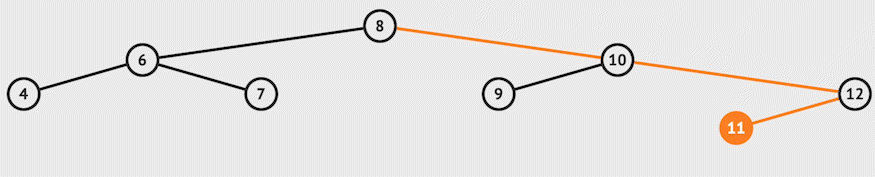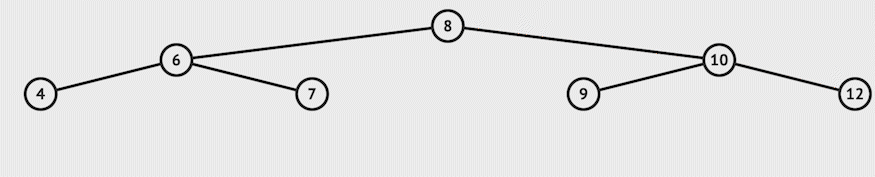
1. Node to be deleted is a leaf node:
In this case, it will just change the leaf node to None.
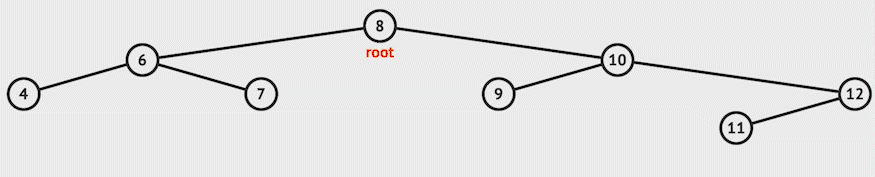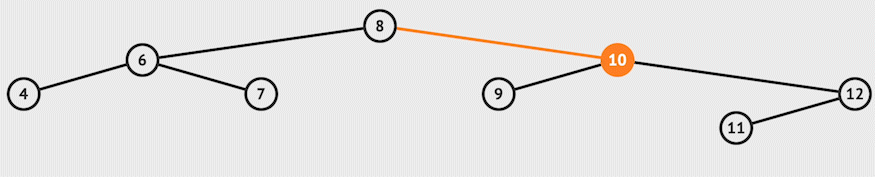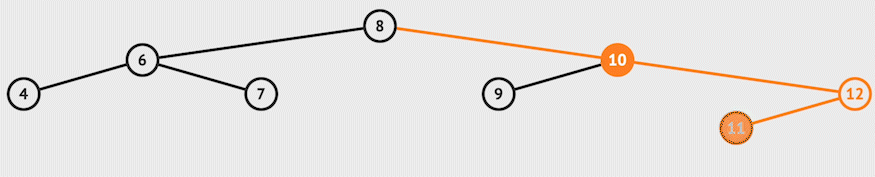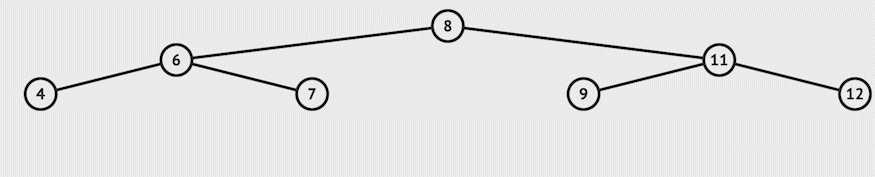
For example, let us delete 11 from the example:-

2. Node to be deleted has only one child:
In this case, it returns the non-empty child to replace the node.
For example, let's say we want to delete 12 in the example:-

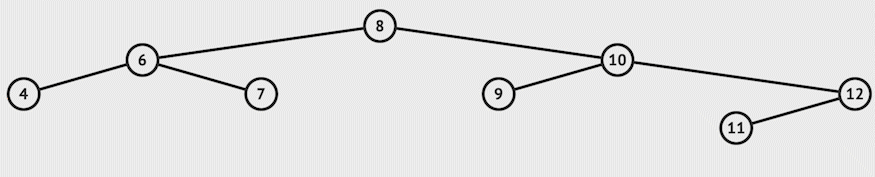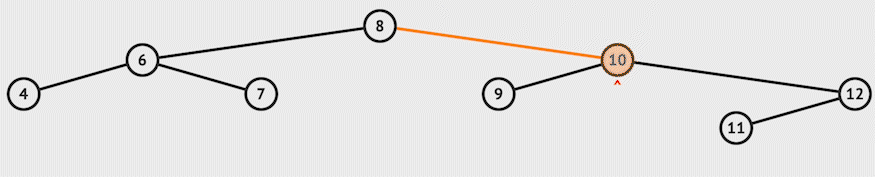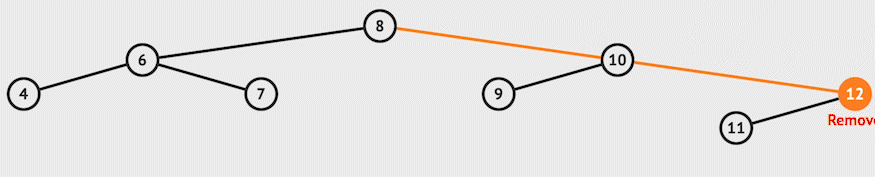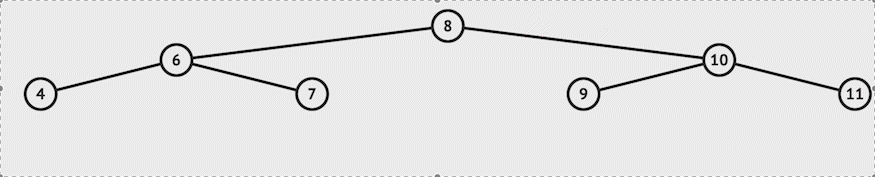
3. Node to be deleted has both child:
In this case, in order to conserve the BST properties, we need to replace it with either :

1. The greatest value node in it's left subtree (or)
2. The smallest value node in it's right subtree
   and return the root.

In our code, we will be going by the 2nd way, which is replacing the node value with its in-order successor value. _find_min() function will find the minimum value in a tree; we will pass node.root to this function to find the successor.

After replacing the node with its successor value, we will call the delete function again on the node's right child to delete this successor value (since this is a duplicate that we no longer need).

For example, let's delete 10 from the example:-

    def delete(self, val):
        self.root = self._delete_recursive(self.root, val)

    def _delete_recursive(self, node, val):
        if node is None:
            return node

        if val < node.val:
            node.left = self._delete_recursive(node.left, val)
        elif val > node.val:
            node.right = self._delete_recursive(node.right, val)
        else:
            # Case 1 & 2: Node with no child or only one child
            if node.left is None:
                return node.right
            elif node.right is None:
                return node.left

            # Case 3: Node with two children
            successor = self._find_min(node.right)
            node.val = successor.val
            node.right = self._delete_recursive(node.right, successor.val)

        return node
        
    def _find_min(self, node):
        current = node
        while current.left is not None:
            current = current.left
        return current

Time Complexity

1. Search:-
   Worst Case: O(n)
   Average Case: O(h), where h is the height of the tree
2. Insert:-
   Worst Case: O(n)
   Average Case: O(h), where h is the height of the tree
3. Delete:-
   Worst Case: O(n)
   Average Case: O(h), where h is the height of the tree