Chomsky Hierarchy
In this article, we have defined and explained Chomsky Hierarchy which orders the different languages in Theory of Computation. It is also known as Chomsky Schutzenberger Hierarchy.
Table of contents:
- Chomsky Hierarchy
- Meaning of Chomsky Hierarchy
- Modified / Complete Chomsky Hierarchy
Let us get started with Chomsky Hierarchy.
Chomsky Hierarchy
This table gives you the idea of the different Languages in Theory of Computation and the position of Context Sensitive Language:
| Type | Language | Automata Machine | Power |
|---|---|---|---|
| Type 0 | Recursively Enumerable | Turing Machine | Strongest |
| Type 1 | Context Sensitive | Linear Bounded Automaton | Stronger |
| Type 2 | Context Free | Pushdown Automaton | Strong |
| Type 3 | Regular | Finite State Automaton | Weak |
The above table is known as Chomsky Hierarchy and was first formed in 1956 by Noam Chomsky. It was presented in a paper titled "On Certain Formal Properties of Grammars, Information and Control" in 1959.
The table is also named as "Chomsky Schutzenberger Hierarchy" in honor of another Computer Scientist named Marcel Paul Schutzenberger who played a major role in development of Theory of Computation.
Meaning of Chomsky Hierarchy
Chomsky Hierarchy defies the position of four different types of Languages in Theory of Computation. To visual Chomsky Hierarchy, go through this set diagram:
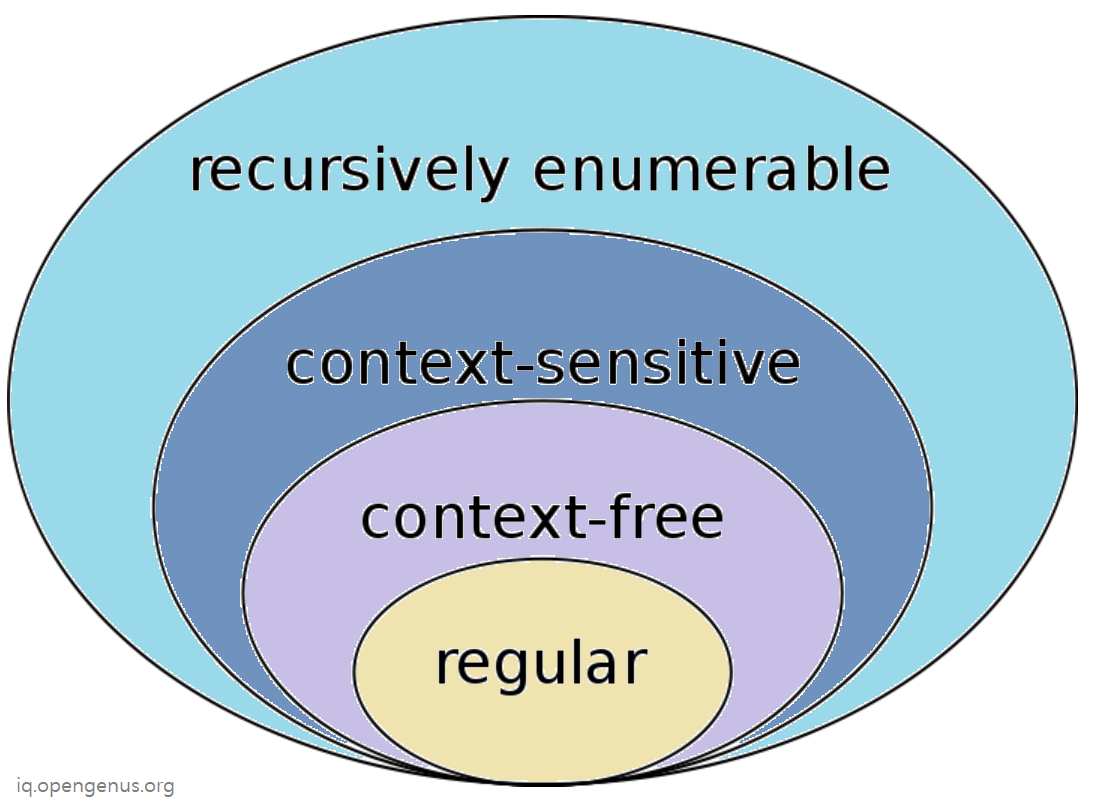
In short:
- Recursively enumerable Language is the largest set.
- Context Sensitive Language is a subset of Recursively enumerable Language
- Context Free Language is a subset of Context Free Language
- Regular Language is a subset of Context Free Language
Type 0
Type 0 Language is the strongest class of Language is Theory of Computation. Formally, it is known as Recursively Enumerable Languages.
It involves all languages that can be generated using a Turing Machine. Turing Machine is the foundation of Computer Science and is the theoretical model representing Modern Computers and Quantum Computers as well.
Type 1
Type 1 Language is a subset of Type 0 language. So, a Type 1 Language is always a Type 0 Language but a Type 0 Language is not always a Type 1 Language.
Type 1 Language is known as Context Sensitive Languages and are weaker than Type 0 Languages. These are the set of Languages that can be generated using Linear Bounded Automaton.
Type 2
Type 2 Language is a subset of Type 1 language. So, a Type 2 Language is always a Type 1 Language but a Type 1 Language is not always a Type 2 Language.
Type 2 Language is known as Context Free Languages and are weaker than Type 1 and Type 0 Languages. These are the set of Languages that can be generated using Pushdown Automaton.
Type 3
Type 3 Language is a subset of Type 2 language. So, a Type 3 Language is always a Type 2 Language but a Type 2 Language is not always a Type 3 Language.
Type 3 Language is known as Regular Languages and are weaker than Type 2, Type 1 and Type 0 Languages. These are the set of Languages that can be generated using Finite State Automaton.
Modified / Complete Chomsky Hierarchy
The original Chomsky Hierarchy does not include Recursive Languages which are accepted by a Total Turing Machine which is a Turing Machine which always halts for any given input.
Recursive Language should idealy appear between Type 0 and Type 1.
| Type | Language | Automata Machine |
|---|---|---|
| Type 0 | Recursively Enumerable | Turing Machine |
| Type 0.5 | Recursive Language | Total/Halting Turing Machine |
| Type 1 | Context Sensitive | Linear Bounded Automaton |
| Type 2 | Context Free | Pushdown Automaton |
| Type 3 | Regular | Finite State Automaton |
With this article at OpenGenus, you must have the complete idea of Chomsky Hierarchy which is an important milestone in Theory of Computation.