Combination Sum problem

In this article at OpenGenus, we have covered the topic on Solving the Combination Sum problem using Backtracking. We have presented the Time and Space Complexity for various cases.

Table of contents:

1. Introduction to Combination Sum problem
2. Solving the Combination Sum problem using Backtracking
3. Time and Space Complexity
4. Conclusion

Introduction to Combination Sum problem

The Combination Sum problem is defined as follows: Given a set of candidate numbers (without duplicates) and a target number, find all unique combinations in candidates where the candidate numbers sum to target. The same repeated number may be chosen from candidates unlimited number of times.

Inputs:
A list of distinct integers candidates
An integer target representing the sum we want to achieve

Expected Output:
A list of all unique combinations of numbers from candidates that add up to target

Constraints:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
All elements of candidates are distinct.
1 <= target <= 40

Solving the Combination Sum problem using Backtracking

class Solution(object):
    def combination_sum(self, candidates, target):
        result = []
        current = []
        start = 0
        self.traverse(result, current, start, target, candidates)
        return result

The main function is combination_sum(), which is called with a list of candidate numbers and a target number. It sets up the list of candidates, the current combination, the starting index. The traverse function is then called to begin the search for combinations.

    def traverse(self, result, current, start, target, candidates):
        if target == 0:
            result.append(list(current))
            return

The function traverse() carries out the bulk of the operations. It is a recursive method that explores every possible combination of candidate numbers. First it determines if the target equals 0, which indicates that the sum of the current list of numbers matches the initial target. If that's the case, it appends the current list to the result list and then call the return statement, which ends the function call and returns the result to the caller.

        if target < 0:
            return

If the target is less than 0, this suggests that that the current combination of numbers sums up to more than the initial target. In this case, it immediately call the return statement without appending anything to the result list.

        for idx in range(start, len(candidates)):
            current.append(candidates[idx])
            self.traverse(result, current, idx, target - candidates[idx], candidates)
            current.pop()

If the target is still greater than 0, the function loops over the candidates starting from the current index. For each candidate, it adds the candidate to the current list and recursively calls the traverse() function with the reduced target number. This is where the function explores each possible combination.

After the function has explored all combinations starting with the current list, the function backtrack by calling current.pop() and remove the last added candidate from the current list.

Here is the entire code block for reference

class Solution(object):
    def combination_sum(self, candidates, target):
        result = []
        current = []
        start = 0
        self.traverse(result, current, start, target, candidates)
        return result

    def traverse(self, result, current, start, target, candidates):
        if target == 0:
            result.append(list(current))
            return
        if target < 0:
            return
        for idx in range(start, len(candidates)):
            current.append(candidates[idx])
            self.traverse(result, current, idx, target - candidates[idx], candidates)
            current.pop()
sol = Solution()
candidates = [2,3]
target = 6
print(sol.combination_sum(candidates, target))

Tree Diagram

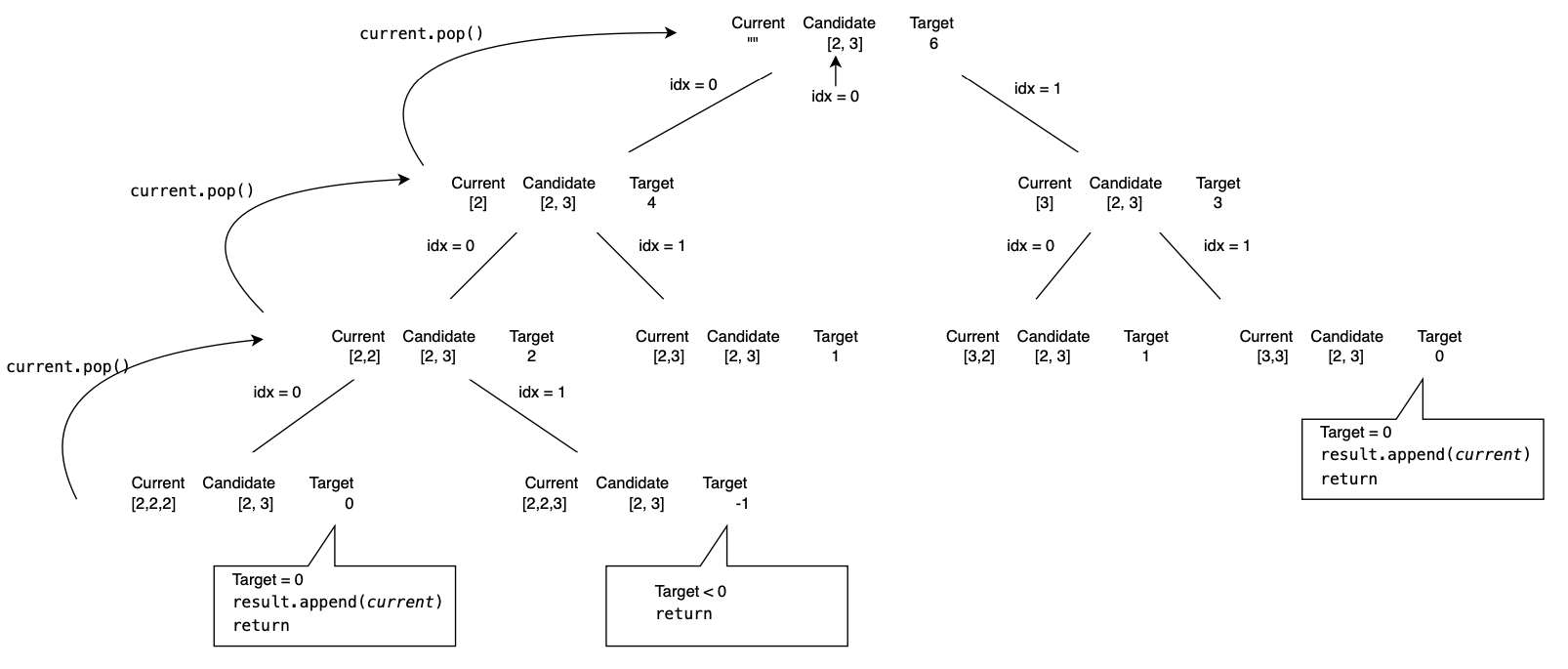
We can illustrate how the program work by using the tree diagram above. At the top of the tree combination_sum() is called to execute the program. We initialise the value of result, current, start, target and candidates here.

Next the goal test is performed, we checked whether target = 0 (current list is appended to result list and the return statement is called) or target < 0 (call the return statement without appending anything to the result list).

The program then loop through each element of the candidate list. It then append the current element of the candidate to the current list. The program recursive call the traverse function and traverse the down the tree in a Depth First Search manner.

Once we reach the bottom of the tree, the program will backtrack one level up the tree by calling current.pop() to undo the previous candidate selection from the current list.

The program end when all possible combination had been explored.

Time and Space Complexity

The time complexity is O(N^(T/M)) where:

N is the number of candidates,
T is the target value,
M is the minimum value in the candidates.

This is the worst-case scenario, in which we must go over each combination sum individually. This occurs when we have the least number of candidates and the target number is the largest. Backtracking algorithms will try every conceivable combination, which in this case is N^(T/M).

The space complexity is O(T/M). This is because, in the worst-case scenario, adding the smallest number up to the target would need storing T/M elements. This happens when the depth of the recursive call stack reaches its limit.

Conclusion

One way of improving the efficiency of the program is by sorting the candidate numbers before we solve the problem. This step is not required for solving the problem, but it can help improve efficiency by allowing us to stop the search as soon as the sum of the current combinations exceeds the target.

With this article at OpenGenus, you must have the complete idea of solving the Combination Sum problem using Backtracking.