Context Free Language (CFL)

In this article, we have explained the idea of Context Free Language (CFL) along with different properties of Context Free Language. This is a core concept in Theory of Computation.

Prerequisite: Context Free Grammar (CFG)

Table of contents:

  1. Definition of Context Free Language (CFL)
  2. Properties of Context Free Language
  3. Pumping Lemma for Context Free Languages

Let us get started with Context Free Language (CFL).

Definition of Context Free Language (CFL)

G is a Context Free Grammer. The language of G is defined to be the set of all strings in Σ* that can be derived for start variable S in V:

L(G) = { w belongs to Σ* : S => w}

  • A language L is called Context Free Language if there is a Context Free Grammer G such that L(G) = L.

Therefore, in simple terms, the set of all strings that can be generated from Context Free Grammar (CFG) is known as Context Free Language (CFL).

Properties of Context Free Language

The properties of Context Free Languages are:

  • Context Free Language is a superset of Regular Language.
  • Context Free Language can track two properties at max.
  • Closure Properties of Context Free Languages.
  • How to recognize Context Free Language?

Let us explore each property in depth.

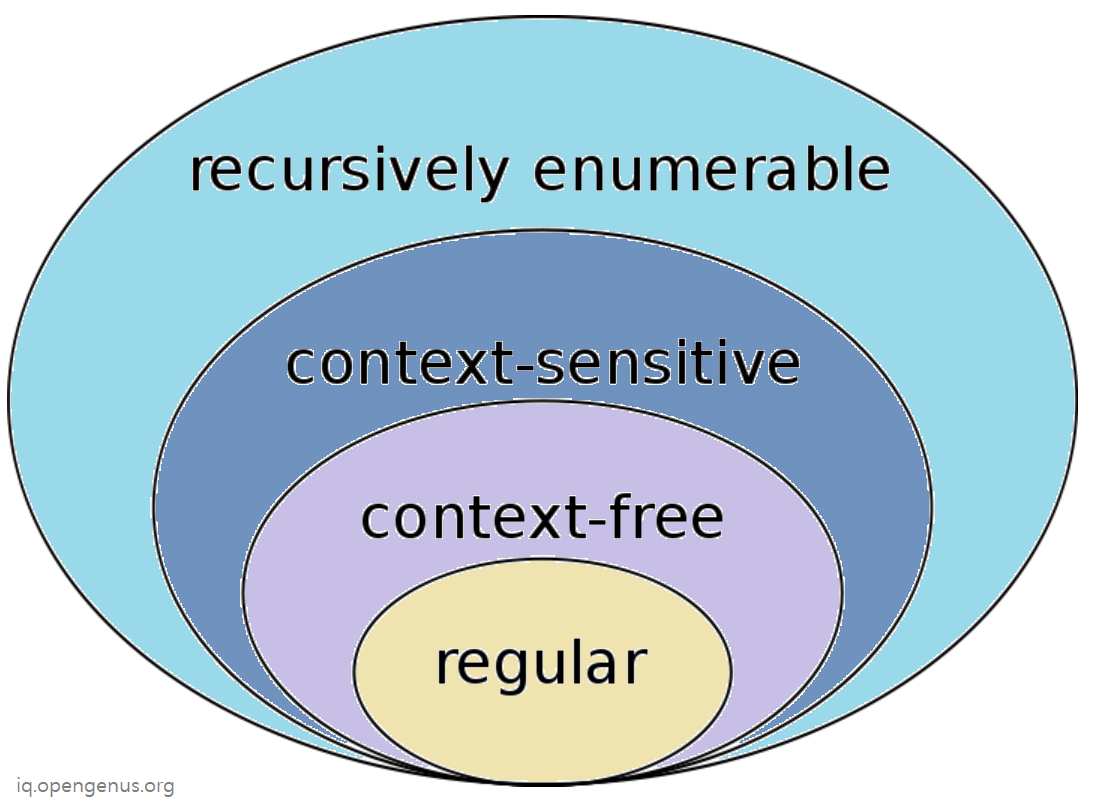
Set of CFL and RL

Context Free Language is a superset of Regular Language.

This means every Regular Language is a Context Free Language but not all Context Free Language is a Regular Language.

Context Free Language is a superset of Regular Language

In short:

  • Recursively enumerable Language is the largest set.
  • Context Sensitive Language is a subset of Recursively enumerable Language
  • Context Free Language is a subset of Context Free Language
  • Regular Language is a subset of Context Free Language

This is captured by:

subset of languages

CFL can track two properties

Regular Languages can track one property at max. So, it can generate a Language that has even number of character A.

Context Free Languages can track two properties at max. So, it can generate a Language that has equal number of two characters say A and B. Such languages cannot be generated using Regular Languages.

If a language has 3 properties such as equal number of three characters, then there languages are not CFLs.

Closure Properties of Context Free Languages

If L1 and L2 are Regular Languages, then:

  • Complement L1 is a Regular Language
  • L1 union L2 is Regular Language
  • L1 intersection L2 is Regular Language
  • L1L2 is Regular Language
  • Kleene star: L1* is Regular Language
  • h*(L1) is Regular Language.

Which of these properties for Regular Language hold true for Context Free Language as well?

  • L1 union L2 is Context Free Language
  • L1L2 is Context Free Language
  • Kleene star: L1* is Context Free Language
  • h*(L1) is Context Free Language.

Context Free Language is closed in a specific operation if applying the operation on CFL results in a Language that also CFL. Such operations are:

  • Union Operation
  • Concatenation
  • Kleene closure
  • Reversal operation
  • Substitution
  • Prefix operation
  • Quotient with regular language
  • Cycle operation
  • Union with regular language
  • Intersection with regular language
  • Difference with regular language
  • Homomorphism
  • Inverse Homomorphism

Operations under which CFLs are not closed means applying these operations on CFL results in a Language that may not be a CFL. These operations include:

  • Intersection
  • Complement
  • Subset
  • Superset
  • Infinite Union
  • Difference
  • Symmetric Difference

How to recognize Context Free Language?

Pushdown Automata can be used to recognize Context Free Languages (CFL).

Moreover, Pushdown Automata can be used to prove that all Regular Languages are Context Free Languages.

Decidable properties of Context Free Language:

  • Decidable for Membership
  • Decidable for Emptiness
  • Decidable for finiteness

Based on Deterministic properties, Context Free Language can be divided as:

  • Deterministic Context Free Language
  • Non Deterministic Context Free Language

Pumping Lemma for Context Free Languages

The theorem of Pumping Lemma for Context Free Languages is as follows:

Given a Context Free Languages L.
There exists an integer p (pumping length) >= 1 such that for every string STR in L with length of STR >= p can be written as STR = UVWXY provided:

  1. VX is not null / empty string
  2. length of VWX <= p
  3. for all i >= 0, UViXYiZ is a part of L.

Note we are pumping two substrings V and Y. In Pumping Lemma for Regular Languages, we were pumping only one substring Y.

Following image will help you understand this theorem:

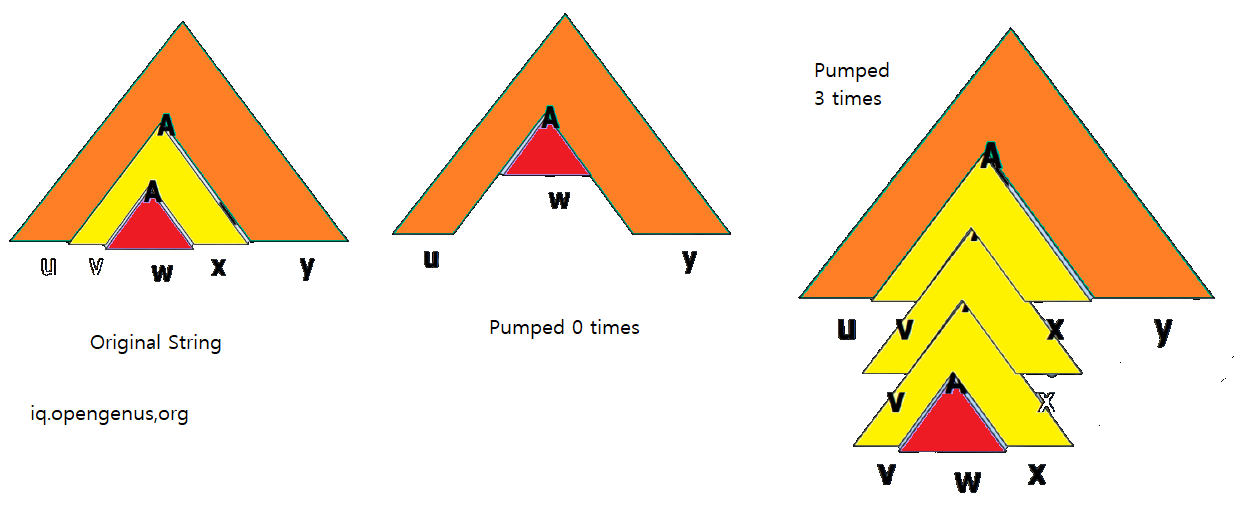
pumping-lemma-cfg

To prove this, you need to have knowledge on Chomsky Normal Form (CNF) and Parse Tree.

With this article at OpenGenus, you must have a strong idea of Context Free Language (CFL).