In this article, we have explained the concept of Context Sensitive Grammar along with examples and properties of it. We have explained the use of Context Sensitive Grammar in Natural Languages as well.

Table of contents:

1. Definition of Context Sensitive Grammar
2. Examples of Context Sensitive Grammar
3. Properties of Context Sensitive Grammar
4. Application of Context Sensitive Grammar

Prerequisite: Context Free Grammar: A grammar which is weaker than Context Sensitive Grammar.

Let us get started with Context Sensitive Grammar.

Definition of Context Sensitive Grammar

Context Sensitive Grammar is defined as a 4 tuple G = (V, Σ, R, S) where:

1. V is a finite set of elements known as variables.
2. Σ is a finite set of elements known as terminals
3. V ∩ Σ = Null (empty set)
4. S is an element of V and is known as start variable.
5. R is a fine set of elements known as Production Rules. Each rule is like aAb -> ayb where A is in V, a and b is in (V union Σ) and y is in (V union Σ)⁺.

Note the difference from Context Free Grammar is in the Production Rules R only.

The rule S -> empty is allowed only for the starting symbol appearing only on the left side of the rule.

Examples of Context Sensitive Grammar

We have presented two examples of Context Sensitive Grammar:

• Example 1: A language which can be generated by both Context Sensitive Grammar and Context Free Grammar
• Example 2: A language which can be generated only by Context Sensitive Grammar and not by Context Free Grammar or Regular Grammar.

Example 1

Example of a Context Sensitive Grammar:

G = (V, Σ, R, S)

V = {S, T}
Σ = {a, b, c}
S is the starting symbol.

R is the set of following Rules:

S -> aTb
S -> ab
aT -> aaTb
aT -> ac

The corresponding Context Sensitive Language is as follows:

L(G) = {ab} union {aⁿcbⁿ | n > 0}

Example 2

Consider a Language where aⁿbⁿcⁿ. For this, we need Context Sensitive Grammar.

We cannot generate this language with Context Free Grammar because it keeps track of only two properties while in this case, we have 3 properties that is count of a, b and c. Similarly, Regular Grammar cannot be used as it is weaker than Context Free Grammar and tracks only 1 property.

The rules of Context Sensitive Grammar for this language will be:

S -> abc
S -> A
A -> aABc
A -> abc
cB -> Bc
bB -> bb

For example, if N=3, then the resultant string will be aaabbbccc and the derivation using our Context Sensitive Grammar will be:

S->A
-> aABc
-> aaABcBc (using Rule: A->aABc)
-> aaabcBcBc (using Rule: A->abc)
-> aaabBccBc (using Rule: cB->Bc)
-> aaabBcBcc (using Rule: cB->Bc)
-> aaabbcBcc (using Rule: bB->bb)
-> aaabbBccc (using Rule: cB->Bc)
-> aaabbbccc (using Rule: bB->bb)

With this, we have our resultant string aaabbbccc.

Note, this Language cannot be generated by Context Free Grammar or Regular Grammar but this is possible with Context Sensitive Grammar which is more powerful.

Properties of Context Sensitive Grammar

Properties of Context Sensitive Grammar are:

All Context Free Languages are Context Sensitive Languages.
Not all Context Sensitive Languages are Context Free Languages.

Every Context Sensitive Grammar that does not generate an empty string can be formulated into a weakly equivalent Context Sensitive Grammar in Kuroda Normal Form. Weakly equivalent means that both the Context Sensitive Grammar generate the same set of Context Sensitive Languages.

A Language generated by Context Sensitive Grammar if and only if the strings of the Language is accepted by Linear Bounded Automaton (LBA).

An algorithm to check if a given string STR can be generated from a given Context Sensitive Grammar G is in PSPACE-complete. This means it is a hard problem and if it is solved in polynomial time then, it will imply P = NP which is a long standing problem in Computer Science.

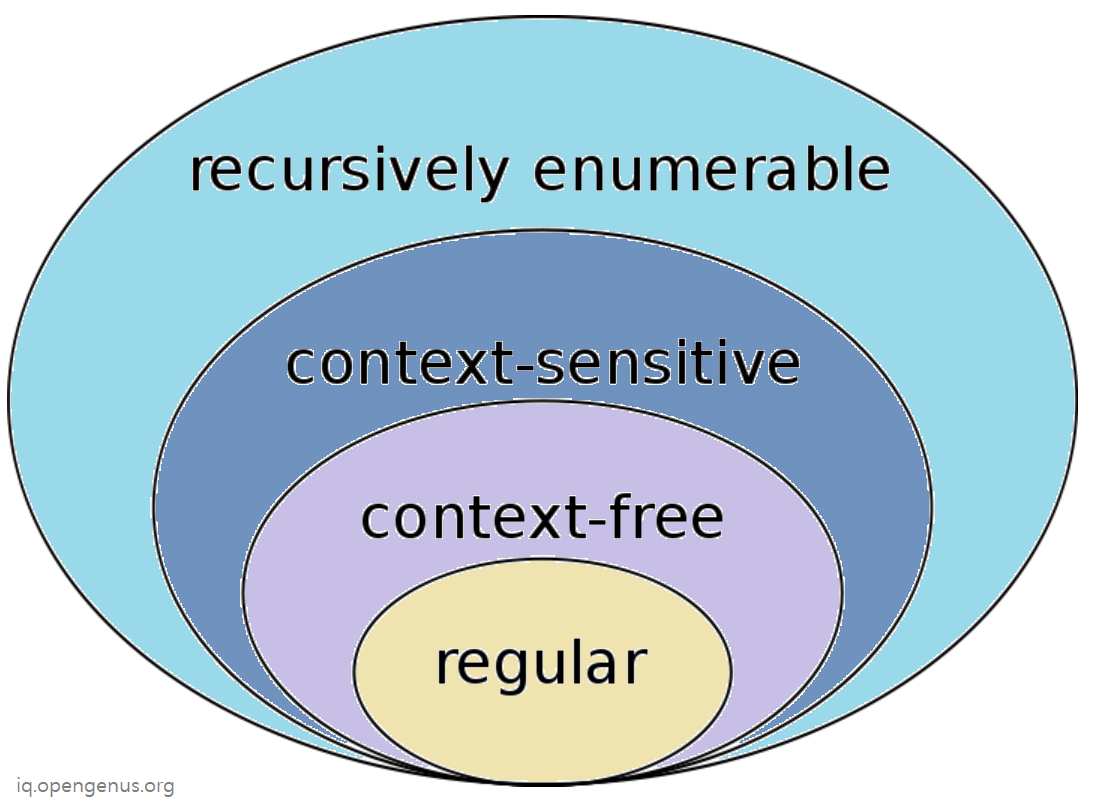
This table gives you the idea of the different Grammars in Theory of Computation:

Type	Grammar	Automata Machine	Grammar Rules
Type 0: Unrestricted	Recursively Enumerable	Turing Machine	a -> b
Type 1: CS	Context Sensitive	Linear Bounded Automaton	aAb -> ayb
Type 2: Context Free	Context Free	Pushdown Automaton	A -> y
Type 3: Regular	Regular	Finite State Automaton	A -> a and A -> aB

The above table is known as Chomsky Hierarchy and was first formed in 1956.

In short:

• Recursively enumerable Language is the largest set.
• Context Sensitive Language is a subset of Recursively enumerable Language
• Context Free Language is a subset of Context Free Language
• Regular Language is a subset of Context Free Language

This is captured by:

Application of Context Sensitive Grammar

Context Sensitive Grammar is more powerful than Context Free Grammar.

Natural Language cannot be modeled using Context Free Grammar but it can be generated using Context Sensitive Grammar.

The problem is Context Sensitive Grammar is:

• CSG is much more powerful than a grammar needed for Natural Language.
• Decision problem for CSG is PSPACE-complete.

For this reason, Context Sensitive Grammar is not usually used to generate Natural Language but it can be used to do so easily as every Natural Language can be modeled as a CSG.

A lesser powerful version of Context Sensitive Grammar known as "Linear Context Free Rewriting Systems" is used to generate Natural Languages.

Research in Computational Linguistics is on producing classes of languages that are weaker than Context Sensitive but stronger than Context Free so that the decision problem can be solved in feasible time. This has resulted in many grammars like Combinatory Categorial Grammar, Tree Adjoining Grammar, Linear Context Free Rewriting Systems, Range Concatenation Grammar and others.

With this article at OpenGenus, you must have the complete idea of Context Sensitive Grammar.