Creating HD Wallet from Seed
In this article, we learn how a Bitcoin HD Wallet is created from a generated seed.
Table of contents.
- Introduction.
- Deriving a Private Child Key.
- Extended Keys.
- Deriving a Public Child Key.
- Summary.
- References.
Prerequisites
Introduction.
Deterministic wallets solve the issue of address reuse and management of multiple keys by using a single seed that can be a 128, 256, or 512-bit random number as the source for all generated keys.
Now, why is reusing wallet addresses unsafe;
First, reusing a wallet address shows a pattern of behavior, for example, in the case of online shopping, and ill-intentioned organization or person can use the information to display targeted intrusive advertisements, another example is in trading cryptocurrencies, in this case, it is easy for one to copy or counter your trading strategies.
Secondly, we said that Bitcoin is transparent and at the same time allows users to remain anonymous. Reusing the same address for transactions hinders anonymity meaning other parties such as governments can follow up on your transactions.
Thirdly, reusing addresses exposes one's financial status to the public, for example, anyone can know how much you make, and what you spend that money on and later use this information to their advantage.
Also, having multiple addresses protects you from getting hacked, meaning if we have multiple wallets and addresses, even if we lose keys to a single one, we still have the rest. It is not wise to keep all our eggs in a single basket.
These are just a few of the implications among many others.
Bitcoin HD wallets make it even easier to derive multiple keys from a single seed by using hierarchical determinism whereby the parent key is used to derive a sequence of children's keys, that in turn are used to generate grandchildren keys, each grandchild can also generate a great-grandchild, this continues infinitely as we go down the tree.
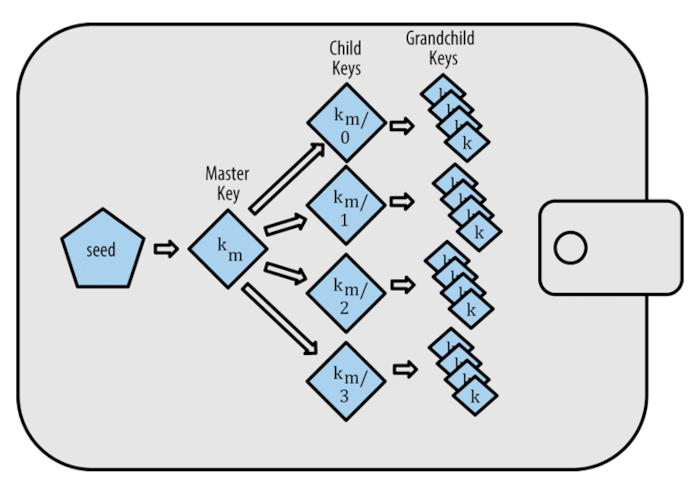
As we can see from the image above, all keys are deterministically generated from the seed. This makes it possible for users to re-create a new HD wallet given a seed and any compatible HD wallet. This makes it easier to backup, store, import, and export HD wallets with millions of keys using s single root seed.
The following demonstrates the process involved in creating a master key and the master chain code for an HD wallet;
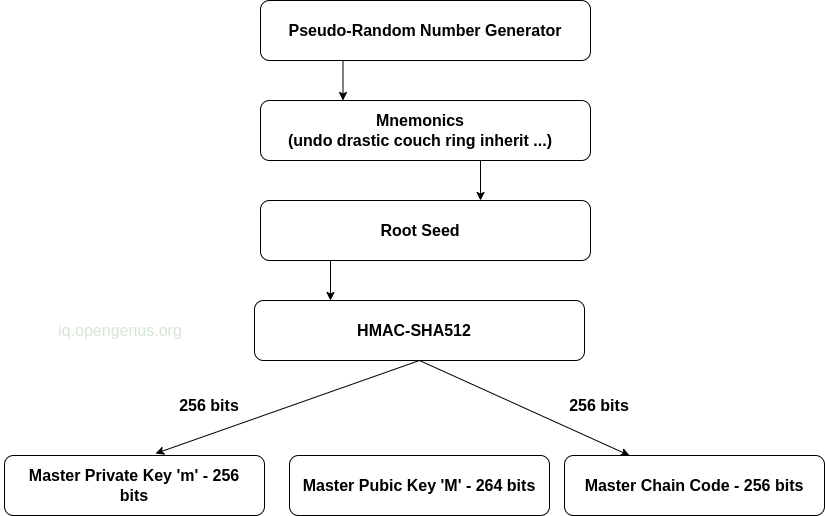
Above, the root seed in the input to the HMAC-SHA512 hashing algorithm, the result is a hash that we will use to create a private key and a master chain code. The former is then used to generate a corresponding master public key using the elliptic curve multiplication process.
The chain code is 256 bits of entropy. It is used to add randomness to the function used to create children's keys from parents. This makes it impossible for malicious parties to determine sibling keys given a single child key. The root of the chain code is derived from the wallet's seed.
The master chain code is a result of the hashing done to the root seed.
The master chain code together with the master private key is used to create the extended public key.
The master private key is a 256-bit key that is generated from the seed phrase. It allows for the creation of an infinite number of keys in the wallet as we can see from the first image. The master key is the root of the whole deterministic wallet and from it, we derive the master public key.
The master public key is derived from the master private key. In this case, even if a public key is exposed, the funds cannot be lost. They don't have access to the private key meaning an Ill-intentioned can only view transactions related to the key.
The master public key is used to generate an infinite number of public keys which in turn are used to generate different wallet addresses. This allows us to use them without having to back them up. In this case, if a key is lost we can start from the seed and recover a wallet in its entirety.
In this article, we learn how to derive a child's private key and public keys in Bitcoin.
Deriving a Private Child Key.
A Child key derivation(CKD) function is used to derive child keys from parent keys. These functions are based on one-way functions(trapdoors) that combine the parent private or public key(1), a chain code(2), and an index number(3).
The chain code introduces randomization to the process such that only knowing the index and a child key is not enough to derive other child keys, since the original chain code seed(root seed) is generated from the original seed while subsequent child nodes are derivations of the parent chain code. Knowledge of the chain code is important to be able to find siblings of a child key.
Now, to generate children keys, parent keys, the chain code, and the index are combined and hashed using the HMAC-SHA512 hashing algorithm. This results in a 512-bit hash, which is then split into two 256-bit halves. The right becomes the chain code while the left bits are deed to the parent private key to produce a child private key.
The process is demonstrated in the image below;
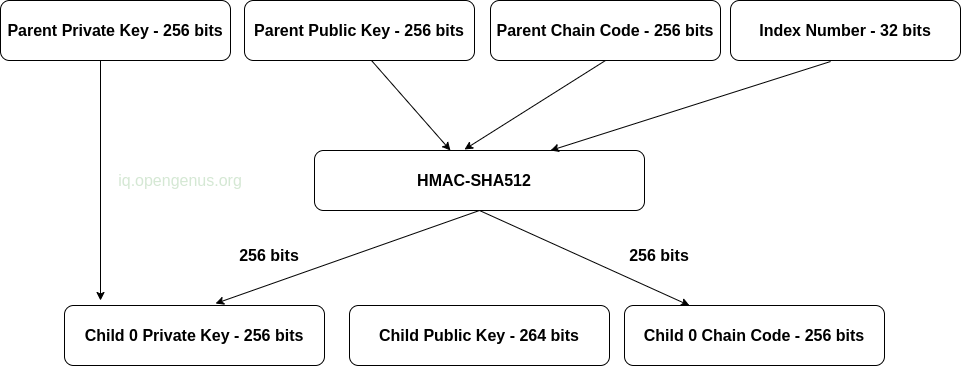
As we can see from the above image, chaining indexes allows us to extend the parent and create other children in the sequence, meaning that a parent in the tree can have about 2^31 children which is half of 2^32, the remaining half is reserved for another derivation.
Extended Keys.
These are a combination of a private/public key and a chain code. They are used to create children and generate branches in the HD wallet tree structure. They are stored and represented as a concatenation of 256-bits keys and a 256-bit chain code that for a 512-bit sequence.
Extended keys can be extended private or extended public keys. The former is a combination of a private key and the chain code and is used to derive child private keys, while the latter is a combination of the public key and the chain code and they are used to derive child public keys.
These keys use the Base58Check encoding algorithm. This makes it easy to import or export keys between compatible HD wallets.
The following is an example of an extended private key that is encoded using the Base58Check encoding algorithm

Deriving a Public Child Key.
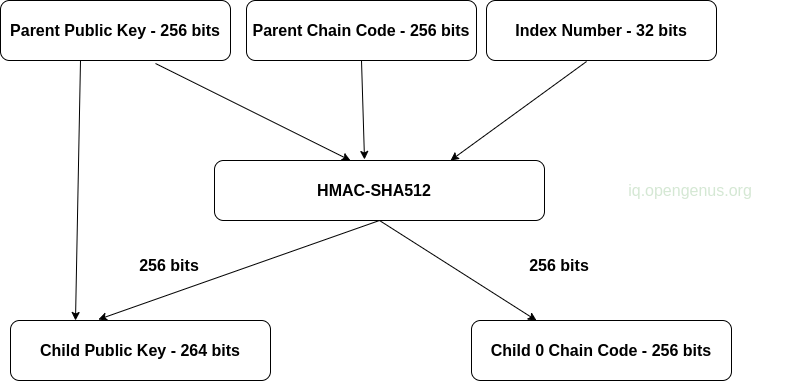
HD wallets allow us to derive public child keys from public parent keys without the need for private keys. To derive a public key, we can either use the child private key or the parent public key. Therefore extended public keys are used to derive all public keys in a branch of the HD wallet structure. This allows the creation of secure public-key deployments whereby a server stores a copy of the extended public key and no private keys.
This is applicable in cases where we only want to send funds to a wallet but not be able to spend them. For example, we can store an extended public key online which allows a user to be able to receive funds but not spend them, to spend then an offline extended private key is used. This can also be used in online payment systems such as e-commerce applications whereby we store an extended public key on a web server serving the app. Each transaction will generate a different wallet address. Now, even if the server is compromised by malicious users, they won't be able to find the private key since it will be stored offline.
The following image demonstrates how an extended parent public key is used to create a child public key;
Summary
The child's private keys are indistinguishable from non-deterministic random keys since the function used in the one-way meaning that the child key cannot be used to derive the parent key. Also, it cannot be used to find any of its siblings.
Without a chain code, a child key cannot be used to derive any grandchildren. In this case, we need both the private key and the child chain code to be able to start a new branch and derive grandchildren.
With this article at OpenGenus, you must have the complete idea of Creating HD Wallet from Seed.