Distinct elements in range query with single element updation
In this article, we have explored how to find the number of unique elements in a given range of an array with single updation using Mo's algorithm. We will see the brute force approach, learn some prerequisites and then move to solving the problem in a more efficient manner.
Table of contents:
- Problem Statement
- Brute Force Approach
- Square Root Decomposition
- Mo's Algorithm
- Mo's Algorithm with modification
- Other Approaches
Let us get started with Distinct elements in range query with single element updation.
Problem Statement
Given an array:
Update(i,x) : update ith element with x.
Find(l,r) :Find number of unique elements between lth and rth range.
Eg: let a[10] = { 1,2,3,3,4,3,2,5,6,7} and we need to update a[4] with 9 and find no of unique elements between 1st to 5th elements.Number of unique elements within the given range is 2 i.e, 2 and 4 and updated array is : {1,2,3,3,7,3,2,5,6,7}
We can solve this problem using segment trees,fenwick trees, square root decomposition.Let us first focus on brute force approach.
Brute Force Approach
We can traverse the array starting from l and update the counts of all the elements till r.Then return the count of elements.We can also update the element at ith index by replacing it with new value.
#include <iostream>
#include<unordered_map>
using namespace std;
int main() {
cout<<"Enter no of elements\n";
int n;
cin>>n;
int arr[n];
cout<<"Enter elements\n";
for(int i=0;i<n;i++)
cin>>arr[i];
//update at ith index:
int k,no,l,r;
cout<<"enter index and no to update\n";
cin>>k>>no;
arr[k]=no;
for(int i=0;i<n;i++)
cout<<arr[i]<<" ";
cout<<endl;
//FInd no of unique elements btw l and r:
cout<<"Range to find\n";
cin>>l>>r;
unordered_map<int,int> u;
for(int i=l;i<=r;i++)
{
if(u[arr[i]]==0)
u[arr[i]]=1;
}
int c=0;
//unique elements count
for(auto a:u)
{
if(a.second==1)
c++;
}
cout<<"No of unique elements: "<<c<<endl;
}
Output
Enter no of elements
>>16
Enter elements
>>1 2 2 3 4 4 5 5 6 6 6 6 6 6 7 7
enter index and no to update
>>3
>>4
1 2 2 4 4 4 5 5 6 6 6 6 6 6 7 7
Range to find
>>1
>>15
No of unique elements: 5
Analysis:
Time complexity: Worst case: O(N)
Space Complexity: For elements: O(N) , For map: O(N)
We can furthur improve the time complexity using other methods like sqrt decomposition,segment tree, fenwick trees etc.
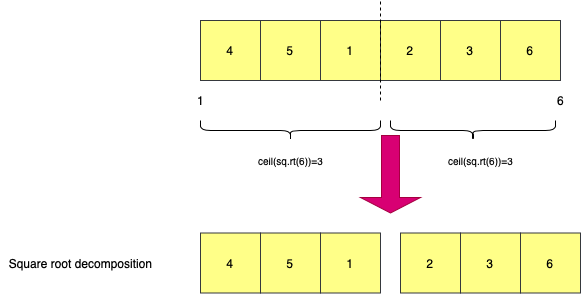
Square Root Decomposition
In square root decomposition , a n-sized array is decomposed or broken down to various smaller subarrays of size ceil(N^1/2) and queries solved for each of them.
Mo's Algorithm
-
An idea based on sqrt decomposition ,Mo's algorithm unlike sqrt decomposition uses only one data structure and keeps track.In certain cases it performs queries fastly.
-
But unfortunately, no updates can be performed while using this method.It initially works for one range but we can reduce or increase the range based on our convenience.
-
For 1 query:
if for many queries we can sort them according to their l and r to prevent repeated jumps
//set storing unique elements only
set<int> s;
vector<int> a;
void add(int k)
{if(s.find(a[k])==s.end())
s.insert(a[k]);
}
void remove(int k)
{if(s.find(a[k])!=s.end())
s.erase(a[k]);
}
To obtain the size of all the unique elements
int Mo(int L,int R,int n)
{
int ML=0,MR=-1;
while(ML > L)
ML-- , add(ML);
while(MR < R)
MR++ , add(MR);
while(ML < L)
remove(ML) , ML++;
while(MR > R)
remove(MR) , MR--;
//returns the size of all the unique elements
return s.size();
}
In the main function:
int main() {
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int c;
cin>>c;
a.push_back(c);
}
int l,r;
cin>>l>>r;
cout<<Mo(l,r,n)<<endl;
}
OUTPUT:
Input:
10
1 3 3 2 4 4 4 4 6 6
0 9
5
Time Complexity: O(N*Q)
where Q means no of queries, N means no of elements.
We can furthur improve it by sorting queries based on l,r and decomposing them,we get:
O(N(N^1/2)+M(N^1/2))
Mo's Algorithm with modification
Mo's Algorithm can be applied only when the array is not prone to updates.But with certain modification , it can be used while being updated too.
Intuition
- Normally Mo's algorithm is 2- Dimensional,i.e. l and r .
- In modification, when there is update, time of queries matters, as in if one query is updated at a point of time ,then everything should be updated w.r.t its timing.
- Modified Mo's algorithm has another added dimension - time
- As there can be repeated updates depending on no of queries , with time , the elements change, so we use time dimension.
Dimensions : l,r and t
Code:
//set storing unique elements only
set<int> s;
int N=1000;int block_size;
vector<int>block(N);
vector<vector<int>> query( N , vector<int> (4, 0));
vector<int> a;
void update(int time,int l,int r)
{
int index=query[time][1];
int val=query[time][2];
int block_no=index/block_size;
//if updated value is unique and within range ,then add to set
if(s.find(val)==s.end())
s.insert(val);
//element at index to be updated if unique is removed from set.
if(s.find(a[index])!=s.end())
s.erase(a[index]);
block[block_no]=block[block_no]+val-a[index];
a[index]=val;
}
//set to add unique elements
void add(int k)
{if(s.find(a[k])==s.end())
s.insert(a[k]);
}
//set to remove elements
void remove(int k)
{if(s.find(a[k])!=s.end())
s.erase(a[k]);
}
Continued after int main in Mo's unmodified version
cout<<"enter no of queries:"<<endl;
int no;
cin>>no;
//query input
for(int i=0;i<no;i++)
{
for(int j=0;j<4;j++)
{ //for update: query[i][0]=i,query[i][1]=x,query[i][2]=time,query[i][3]=1;
//for update: query[i][3]=1 for finding unique elements: query[i][3]=0;
cin>>query[i][j];
}
}
block_size=sqrt(n);
int lef=0,rt=-1,curt=0;
for(int i=0;i<query.size();i++)
{
int x=query[i][0];
int y=query[i][1];
int tt=query[i][2];
while(curt<tt)
{
curt++;
if(query[i][3]==1)
update(curt,lef,rt);
}
while(curt>tt)
{ if(query[i][3]==1)
update(curt,lef,rt);
curt--;
}
while(lef<x)
{
remove(a[lef]);
lef++;
}
while(lef>x)
{
lef--;
add(a[lef]);
}
while(rt<y)
{
rt++;
add(a[rt]);
}
while(rt>y)
{
remove(a[rt]);
rt--;
}
cout<<"no of distinct elements in query \t"<<s.size()<<endl;
}
}
Time & Space Complexity
Time Complexity:O(q*N^2/3)
Best Time complexity:O(2 * N^2)^1/3
Space Complexity : O(N) for elements,O(q) for queries , O(N) for set.
Now we know how to find the number of unique elements in the given range and also perform single updation using Mo's Algorithm.We will furthur see different methods to solve this problem like segment trees, fenwick trees etc.
ThankYou!
Other Approaches
1)sqrt decomposition
Divide the array into sqrt blocks ,sort each block,then just binary search for r in each block to find no.of elements greater than r
Complexity:-O(Qroot(N)logN)
2)segment tree with ordered set in each node
Lets say each node consists of ordered set of the range.So u can simply binary search and find no.of elements greater than r
Complexity:-O(Qlog^n)
3)segment tree with each node having a dynamic segment tree
This is similar to the above method.One can have a dynamic segment tree in each node,where that DST[range] gives no.of elements in range.
Complexity:O(nlog^2)
5)persistent segment tree
Build a persistent segment tree such that seg[i:j] gives count of number of elements(values not indices) in (i,j).
So to ans (l,r) :- rthseg[r+1,inf] - (l-1)thseg[r+1,inf]
(Xthseg[i,j] denite no.of elements with values in range(i,j) and indices (1,X))
Complexity :- O(qlogn)
And last method :slight_smile:
6)simple segment tree
See to answer (l,r) if we know no.of elements in range[1,r] and [1,l-1] greater than r,then ans is simply difference of the two
So just process the queries lyk,lets say we have queries :-
(3,5)
(2,4)
So i have to calculate (i,j) which denote no.of elements greater than j in range[1,i]
I mean we have to calculate (2,5),(5,5),(1,4),(4,4)
Now sort these values in decreasing order based on first value
(5,5),(4,4),(2,5),(1,5)
Now lets say we have a segment tree where seg[range] returns no.of elements in range.
So to ans (i,j) we need to have a segment tree of first i elements and query for range[j+1,inf]
So as we process it backwards we can easily process all queries(ie first u have seg tree for first 5 elements ,so if want for 4 elements delete the 5th element)
Complexity :- O(qlogn)
With this article at OpenGenus, you must have the complete idea to solve this challenging problem: Distinct elements in range query with single element updation.