ECDSA in Bitcoin
In this article, we learn how the ECDSA algorithm is used in Bitcoin to generate public keys and sign transactions thereby securing the blockchain.
Table of contents.
- Introduction.
- Generating a public key.
- Signing a transaction.
- Summary.
- References.
Prerequisites.
ECDSA: Key generation, Signing, and verifying transactions.
Introduction
In the previous articles, we learned about Elliptic Curve Cryptography, how it works, mathematical concepts behind it. We also saw how it is difficult and computationally demanding to be able to recover the private key just by having the public key.
We learned what a trap door is and saw its application to public-key cryptography.
In this article, we will see how ECDSA cryptography is used in the Bitcoin blockchain. We will use the elliptic curve theory discussed in previous articles to create public keys and sign and verify transactions, just like the bitcoin blockchain does.
Generating a public key.
Consider the following image, it demonstrates how a public key is placed inside a locking script in output.
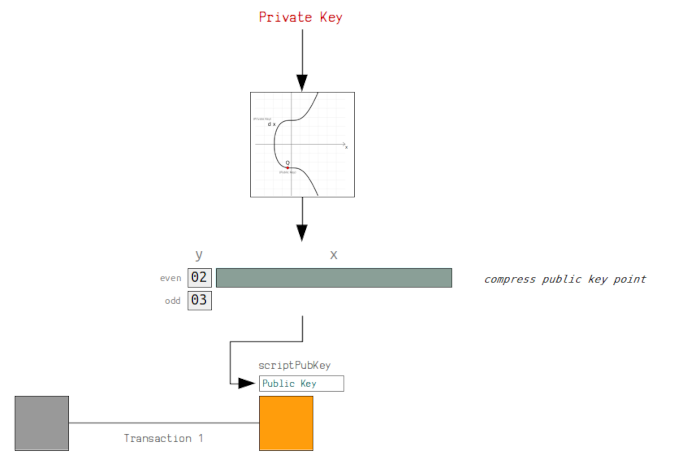
As mentioned previously, the public key is the multiplication between the generator point and the private key. It is a point on the elliptic curve comprising of x, y coordinates.
private key = 112757557418114203588093402336452206775565751179231977388358956335153294300646
public key = {
x: 33886286099813419182054595252042348742146950914608322024530631065951421850289,
y: 9529752953487881233694078263953407116222499632359298014255097182349749987176
}
Bitcoin converts these into hexadecimal format as shown below;
public key = {
x: 4aeaf55040fa16de37303d13ca1dde85f4ca9baa36e2963a27a1c0c1165fe2b1,
y: 1511a626b232de4ed05b204bd9eccaf1b79f5752e14dd1e847aa2f4db6a52768
}
public key = 4aeaf55040fa16de37303d13ca1dde85f4ca9baa36e2963a27a1c0c1165fe2b11511a626b232de4ed05b204bd9eccaf1b79f5752e14dd1e847aa2f4db6a52768
We can prepend zeros as padding if necessary to reach 32 bytes.
Elliptic curves are symmetrical, this means that every x coordinate has two possible y coordinates, one even and the other odd. Therefore we can use a prefix to specify the y coordinates we are using for a point. This means the public key is halved in size and this makes transactions smaller and faster.
Examples of prefixes include;
- 02 - y is even(compressed)
- 03 - y is odd(compressed)
- 04 - the full uncompressed y.
For our public key, we have an even y coordinate, to shorten the key, we use 02 with the full x coordinates as shown below;
public key (uncompressed) = 044aeaf55040fa16de37303d13ca1dde85f4ca9baa36e2963a27a1c0c1165fe2b11511a626b232de4ed05b204bd9eccaf1b79f5752e14dd1e847aa2f4db6a52768
public key (compressed) = 024aeaf55040fa16de37303d13ca1dde85f4ca9baa36e2963a27a1c0c1165fe2b1
To be able to receive bitcoin from the sender these keys are placed inside a locking script on an output transaction. This makes sure the bitcoin can only be spent by the recipient. This information is broadcasted to all network nodes.
Signing a transaction.
In this section, we will learn how a bitcoin transaction is signed ensuring the recipient is the only party able to spend the sent bitcoins. A digital signature from the sender is required from the recipient. It is used as proof that the recipient has the private key for the public key used to lock the bitcoins. Remember, obtaining the private key is near impossible just having the public key.
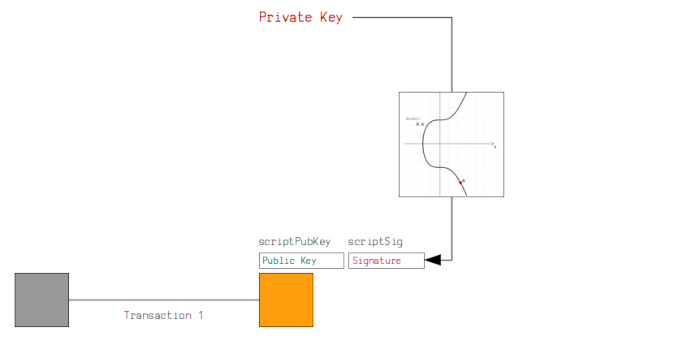
In order to sign a transaction we first have to construct it, this involves specifying the message. Secondly, we use the private key to sign the message and finally package the message inside the transaction.
The following is a demonstration of how transactions are signed in Bitcoin.
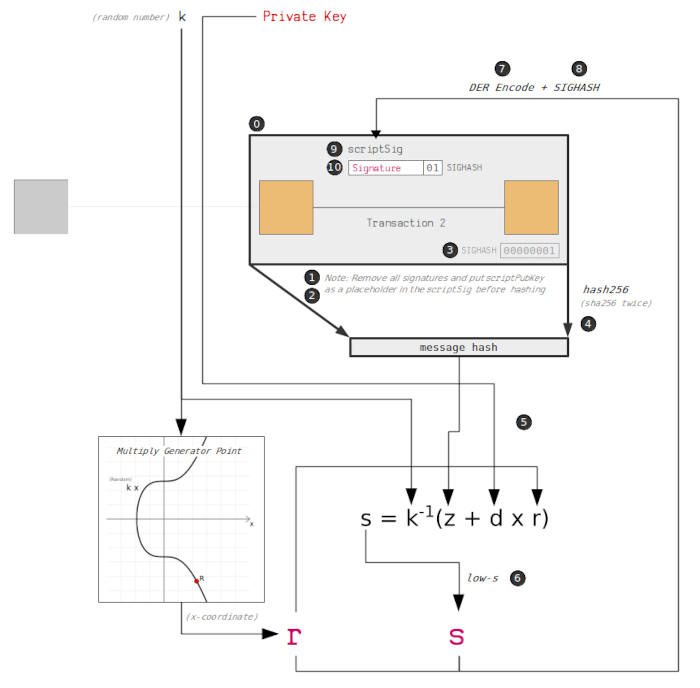
The steps in the image are explained below;
-
Generate the transaction
The first step in a transaction whereby person A wants to send person B some bitcoin is to generate data that will spend the current bitcoin owned by A, this is input data to a transaction that will later create outputs.
In General, we choose inputs we want to spend so that we can later create outputs where we lock the inputs too. -
Removing existing unlocking scripts
Person A, who intends to send coins to person B uses a digital signature to sign the data that describes the movement of coins from he/her wallet to the recipient.
At this stage, we remove the currently created unlocking scripts scriptSigs for inputs to the transaction. -
Place the locking script as a placeholder
We place the input's original locking script at the place where the digital signature is supposed to go, kind of like a placeholder in an input field in a form such as an email address. -
Append the signature hash type to the transaction data
Here we specify the transaction structure we will be signing. Signing involves appending the 4-byte signature hash type SIGHASH at the end of transaction data.
This is demonstrated below;
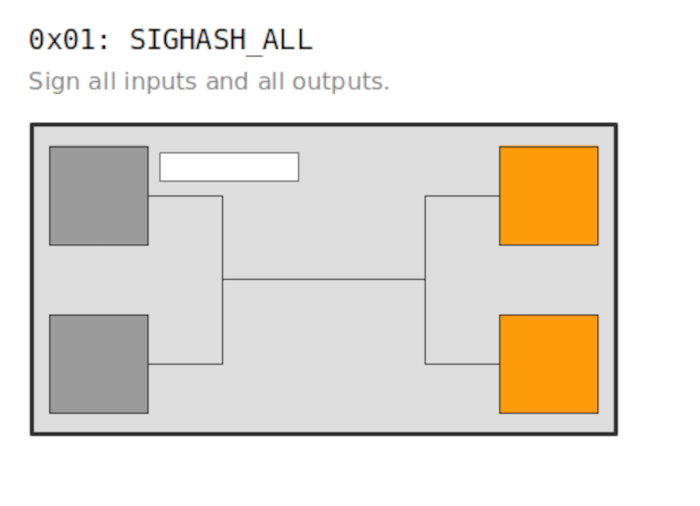 )
)
A common signature hash - SIGHASH_ALL(0x01) indicates that the signature coves all inputs and outputs in a transaction are used. It means that no other party can add any additional inputs or outputs later.
5.Hash the transaction data
At this point, we have a raw unsigned transaction. We use hashing algorithms to create a hash of the transaction. Bitcoin uses double SHA-256
-
Sign the transaction hash
In order to sign the hashed transaction we need a private key - d and a randomly generated number - k. We have mentioned in previous articles why randomization is important. -
Use low-s value
In ECDSA, we can use either a high's value or a low's value in order to generate a valid signature. If we choose one between the two, the other valid value is referred to as an additive inverse of the current value. Since these values are in a finite field n, we will land on the same x-coordinate on the curve of the random point R during verification of the signature.
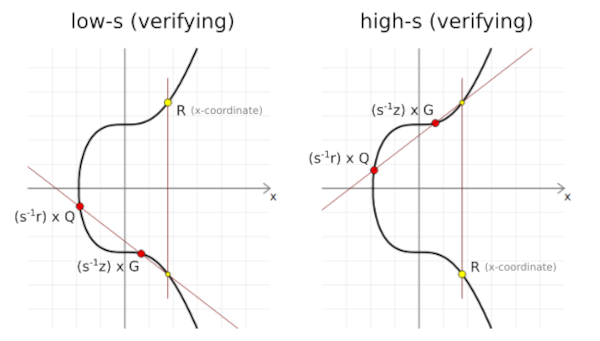
From the image, the additive inverse of s can be used to calculate the opposite points on the curve during the validation of digital signatures, the x-coordinate of the third point will be similar.
This is problematic since it means that we cannot reliably track bitcoin transactions since if anyone can inverse s after a transaction has been sent, the transaction would be changed. To solve this the lows value is used to prevent malleability in bitcoin transactions.
-
Encode the signature using DER
Bitcoin uses Distinguished Encoding Rules(DER) to encode the digital signature. DER involves converting the r and s into hexadecimal values and then adding additional bytes in between as an indication of the length and data type. -
Append the signature hash type to the DER-encoded signature
We append the signature hash type SIGHASH to indicate how much transaction data the signature applies to. Note that this signature hash type should similar to the one selected in the fourth step.
This step makes sure that the signature hash type previously created is not changed. As we explained earlier, signature hash types are responsible for the inputs a transaction can take.
-
Construct the unlocking script
We then place the signature in a script used to unlock the transaction input. -
Insert the unlocking script in the transaction
The final step involves adding the script generated above into a transaction.
The discussed steps apply to all inputs we wish to unlock. This improves the security of transactions in Bitcoin.
Summary
A private key is a randomly generated number. We convert it back to an integer if it is in a hexadecimal format so we can use it in elliptic curve multiplication.
A public key comes as a result of the multiplication between the generator point and the private key.
Elliptic curves are symmetrical, therefore every x coordinate has two possible y coordinates, one even and the other odd.
With this article at OpenGenus, you must have the complete idea of ECDSA in Bitcoin.