Extended Public Key
In this article, we learn how hardened child keys are derived, what key identifiers are, and how to navigate the HD wallet tree structure.
Table of contents.
- Introduction.
- An example.
- Hardened Child Key Derivation.
- Key Identifiers in HD Wallets.
- Navigating an HD Wallet Tree Structure.
- Summary.
- References.
Introduction
In this article on Extended Public keys, we will learn about Extended Public keys, a combination of a public key and a chain code used to create children and generate branches in the HD wallet tree structure stored as a 512-bit(256-bits each, for the keys and chain code) sequence.
In this article, we will look at a practical application of Extended public keys and the shortcomings, we will see how the shortcomings are managed through hardened child key derivation and how to navigate an HD wallet tree structure.
An extended key could be a private or public key that can be used to derive new keys in HD wallets. That is, given a single extended private or public key, we can use it as a source for all child public keys. An Extended public key - Xpub is a Bitcoin standard that was introduced by BIP 32. BIP 32 is a Bitcoin Improvement Proposal that introduced HD wallets and Extended keys to Bitcoin. For more on this, refer to the Github link in the references section.
We learn that public keys can be known to the public without any severe implications. On the other hand, sharing extended public keys should only be to trusted parties. This is because it exposes one to the situation whereby an untrusted party can derive all the child public keys from the xpub and therefore view all past and future transactions of the owner.
In most cases, users use xpubs to receive funds that go to cold storage directly. In such cases, the private key remains offline while the extended public key sits on a server generating new wallet addresses for each transaction.
An example.
Consider the following scenario, Alice has an online shop where buyers come to buy stuff. Buyers usually pay Alice in Bitcoins, Alice hooked her bitcoin wallet address to the site so that her customers can send her money for fulfilled orders. As time went by, Alice managed to acquire more customers, meaning more transactions were being processed and more funds were being sent to her wallet.
More customers meant more transactions with the same bitcoin wallet address, at times, Alice would confuse and mix up orders because of the volume and the similarities of the orders. To solve this Alice adopted an HD Bitcoin wallet, which allowed her to derive public child keys for every transaction without the need for a private key. It also made the management of orders and keys easy. This is because each order sent funds to a unique bitcoin address and keys all were related to a single private key that was kept hidden. This meant that only Alice can spend the bitcoins sent to her using the private key while still using unique wallet addresses for each transaction and receiving funds from buyers.
The use of an HD wallet made it easier to manage keys, export, import, and migrate to new compatible wallets among other benefits. It also meant that the website could be hacked and hackers would turn up empty-handed since the private key is not loaded on the site.
Hardened Child Key Derivation.
In the example, Alice is safe from hackers and can carry out all transactions without fear that funds might be stolen, this is as long as the private key is kept hidden. However, a problem presents itself in that, being able to access the extended public key does not guarantee access to a child's private keys. Since Extended public keys have a chain code, if the child's private key is disclosed, it can be used together with the chain code to derive the rest of the other child's private keys. To make it worse, a child's private key combined with the parent chain code can be used to generate the parent private key. This means that Alice faces a risk of losing all her funds if any child's private key is leaked.
A hardened derivation is a derivation function used by HD wallets to break the relation between a parent public key and a child chain code. This function uses a parent private key to come up with the child chain code, rather than the parent public key. This 'firewall' ensures that a chain code cannot be used to derive a parent or sibling's private key.
The following is an image demonstrating hardened child key derivation;
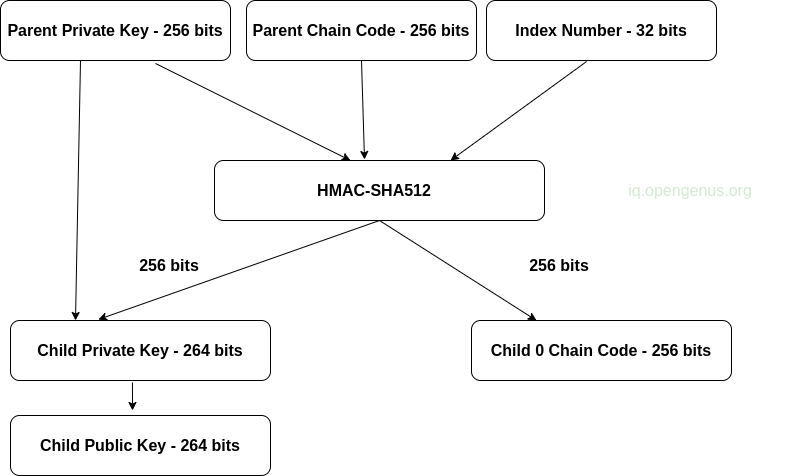
From the image, notice how the hardened derivation function is similar to a normal child private-key derivation, the only difference is that the parent private key is used as input to the hash function. Using this function makes sure that the resulting child's private key and the chain code are different. The branch which is a result of the function is used to produce extended public keys that cannot be hacked since the chain code cannot be exploited to reveal private keys.
Index numbers.
A 32-bit integer is used as the index number in a derivation function. We use the index numbers to distinguish keys generated using normal derivation and hardened derivation function. This is because the index number is split into two ranges the first between 0 and 2^31 - 1 (0x0 to 0x7FFFFFFF) and the second between 2^31 and 2^32 - 1 (0x80000000 to 0xFFFFFFFF). If the index number falls in the first range, the keys are derived using a normal derivation function, on the other hand, if the index lies in the second range, it means that the keys are generated using a hardened derivation function.
Key Identifiers in HD Wallets.
A 'path' is used to identify keys in an HD wallet whereby each level of the tree is separated using a '/' character. Private keys that are derived from the master private key begin with m while public keys derived from the master public keys start with M. This means that the first child's public key will be M/0, and the first grandchild of the public key will be M/0/0
To find out the ancestry of a key, we read from the right until we reach the master key from where it was derived from. E.g, m/n/o specifies a key that is the Oth child of key *m/n which is the nth-child of m.
The following image shows various examples of HD wallet paths;

Navigating an HD Wallet Tree Structure.
In the HD wallet tree structure, each parent extended key can have around 4 billion children whereby the first half(2B) consists of normal children and the other half(2B) consists of hardened children. Each of the children can have other 4 billion children of each branch with 2 billion each, this continues infinitely. The deeper the tree the more difficult it becomes to traverse it.
Two standard BIPs 43 and 44 were proposed to solve this complex issue. We learned about the BIPs and the different types here. The former proposes the use of the first hardened child index as a special identifier to represent the 'purpose' of the tree structure. Based on this, a HD wallet can only use a single level-1 branch of the tree whereby an index number identifies the structure and namespace of the remaining tree by defining its purpose.
The latter proposed a multi-account structure as 'purpose' number 44' under BIP-43, meaning that all HD wallets abiding by this structure are identified using a single tree branch - m/44'/. This BIP proposal consists of the following 5 tree levels;
m / purpose / coin type / account' / change / address index
m is always set to 44'.
coin type specifies the cryptocurrency.
account allows users to subs=divide wallets into different logical accounts for organizational purposes.
change has two subtrees, for creating receiving addresses and change addresses.
address index represents the address index.
The following are various examples of BIP-44 HD wallet structures;

Summary
A child's private key that has been disclosed combined with the chain code can be used to derive all private keys of all children.
To use extended public keys and still keep hackers at bay, we should use derive the key from a hardened parent rather than a normal parent. It is best practice to derive all level 1 children of master keys using a hardened derivation function. This ensures that the master keys are not compromised.