Generating a Bitcoin Private Key

In this article, we learn how to generate a bitcoin private key, that is later used to generate a bitcoin address.

Table of contents.

1. Introduction.
2. Private keys.
3. Generating a Private Key.
4. Summary.
5. References.

Introduction

Cryptography, more specifically public-key cryptography is at the heart of blockchain technology. Hashing is also used to secure transactions and prevent blockchain mutability.

In public-key cryptography also known as asymmetric cryptography, we generate two key pairs, a private key which we keep private and a public key which we share, this key will be used by the recipient together with his/her private key to decrypt the encrypted message.

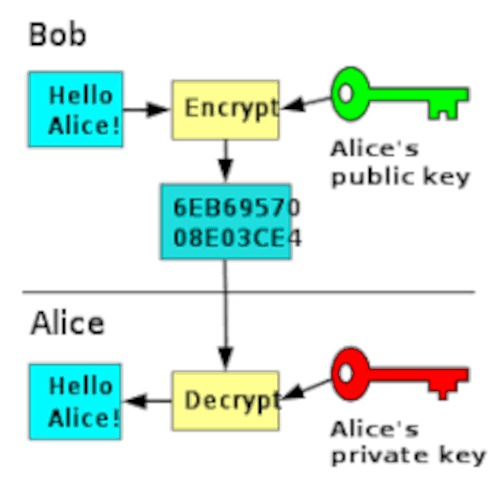
In cryptography, a cryptographic key is randomized data used to scramble data so that it looks random. Plaintext data goes through an encryption algorithm whose result is randomized data(encrypted).

Unlike symmetric cryptography such s ceases cipher where a single key is used to encrypt and decrypt information, asymmetric ensure all challenges encounter using the former such as sharing of keys, and reversal of the encrypted message was solved. Asymmetric cryptography is considered a trapdoor function, whereby it is easy to compute in one direction but impossible to compute in the opposite direction without some key information, in our case this key piece of information is the private key.

In this article, we will learn how to generate a bitcoin private key, we will later use this generated private key to generate a bitcoin address. Usually, private keys are generated by third parties, for example, crypto exchanges and other bitcoin wallets.

Private keys.

This is just a variable used by an encryption algorithm to encrypt and decrypt data. In Bitcoin specifically, it is a 32-byte series of characters that can be converted into any format such as binary, hexadecimal, base64, etc.

As we learned in previous articles, Bitcoin uses the ECDSA algorithm which uses a specific elliptic curve referred to as secp256k1. In this case, we generate a 32-byte key to satisfy the curve parameters, that is, since the curve is in the order of 256 bits, it takes 256 bits as input and returns 256-bit integers. 256 bits is equivalent to 32-bytes(32 * 8 = 256).

The secp256k1 curve also has a specific rule about the size of the key, it should be less than the curve order, also the key should be a positive number.

Generating a private key.

As mentioned, a private key is 32-bytes and it is randomized. To generate a randomized 32-byte string using python, we will use the python random library.

import random

bits = random.getrandbits(256)

key_hex = hex(bits)

private_key = key_hex[2:]

print(private_key)

The output for the above code is as follows;

Each time we run this code we will generate a new randomized private key.

This is good, however, the python random generator library was not built for cryptography. The private key generated in this way uses the current time as the seed meaning that if a malicious user knows the exact time we generated this key then a brute force algorithm would crack this key in a very short time. Remember once coins on the blockchain are stolen, there is no way of recovering them so we should be very careful.

Now let's use a stronger random number generator library referred to as secrets, it is a python module used for generating stronger randomized numbers which we can then use to generate a private key and it was specifically designed for cryptographic operations. For this we write;

import secrets

bits = secrets.randbits(256)

key_hex = hex(bits)

private_key = key_hex[2:]

print(private_key)

We have the following output;

An entropy is randomness generated by an operating system that is used in algorithms that need randomized data. Using the above way to generate a private key is much more secure than the previous since it gets its entropy from the operating system meaning a malicious user would have a hard time finding such since he/she is on a different machine and even with access to the original machine, the task is still very difficult. In this case, the seed is created by the algorithm itself.

We can also use the python PyCryptodome library which implements RSA, the most used algorithm for public-key cryptography. To generate a private key we write;

from Crypto.PublicKey import RSA
key = RSA.generate(2048)

private_key = key.exportKey("PEM")

print(private_key)

The output is shown below;

Above we use a 2048 key length which is the recommended key length for utmost security. This is also very difficult to crack because of some of its features such as the use of symmetric ciphers, authenticated encryption, and strong one-way hashing functions.

Summary

Randomization is very essential to cryptography, especially public-key cryptography. We have used three python libraries one superior to its predecessor for cryptographic work, however, we can also use websites such as random.org and bitaddress.org, these and many more to generate public and private keys. Each has its own way of implementing randomness. The latter is preferred since the code can be downloaded and run locally, this means that no one can know your private key except you.

Private keys should be kept hidden, this means that the owner should be the only one in possession of the key. However, in the case of third parties who generate the private key for its users, it leaves users vulnerable since they are not the only ones with the knowledge of the private key.

With this article at OpenGenus, you must have the complete idea of how to generate a Bitcoin Private Key.