Heapq module in Python
In this article, we will explore the heapq module which is a part of Python standard library. This module implements the heap queue algorithm, also known as the priority queue algorithm. But before proceeding any further, let me first explain what are heaps and priority queues.
Heaps
A heap is a data structure with two main properties:
- Complete Binary Tree
- Heap Order Property
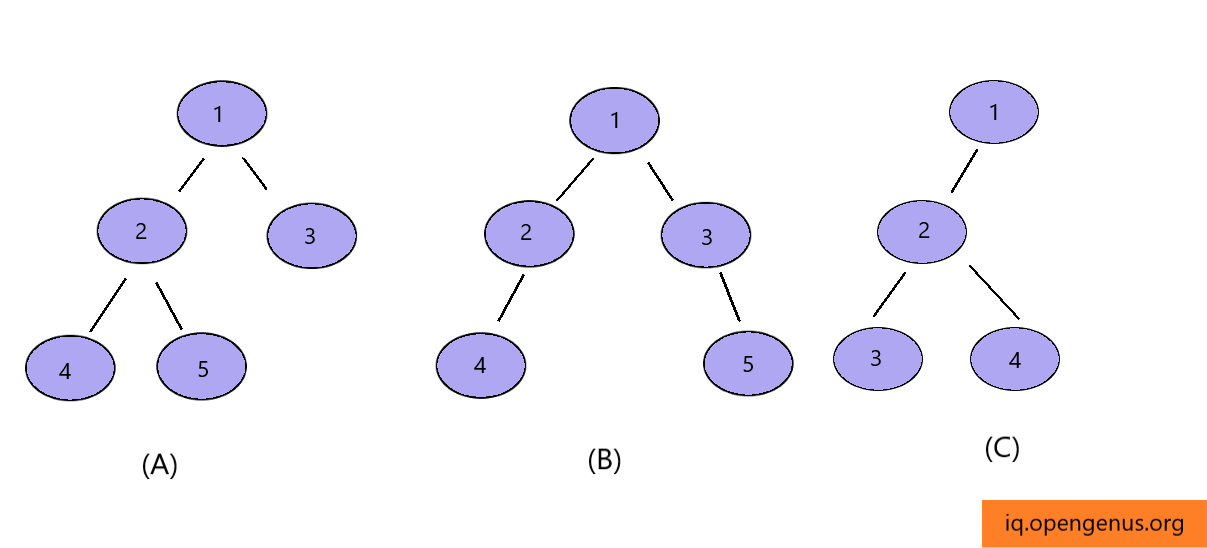
A complete binary tree is a special type of binary tree in which all levels must be filled except for the last level. Moreover, in the last level, the elements must be filled from left to right.
Question
Which of these correctly represents a complete binary tree ?
Heap Order Property - Heaps come in two variants:
- Min Heap
- Max Heap
Min Heap - In the case of min heaps, for each node, the parent node must be smaller than both the child nodes. It's okay even if one or both of the child nodes do not exists. However if they do exist, the value of the parent node must be smaller. Also note that it does not matter if the left node is greater than the right node or vice versa.
Max Heap - For max heaps, this condition is exactly reversed. For each node, the value of the parent node must be larger than both the child nodes.
Priority Queues
Heaps are concrete data types or structures (CDT), whereas priority queues are abstract data structures (ADT). An abstract data types determines the interface, while a concrete data types defines the implementation.
A queue is a FIFO (First In First Out) data structure in which the element placed at first can be accessed first.
A priority queue is a special type of queue in which each element is associated with an additional property called priority and is served according to its priority i.e., an element with high priority is served before an element with low priority. It is most commonly implemented using a heap in O(log n) time.
In Python heapq module, the smallest element is given the highest priority.
Now that we have a basic understanding of the underlying data structures, let's move on to the details of the heapq module.
Implementation
Although heaps are generally represented by trees, it can also be implemented as an array. It is possible because heap is a complete binary tree. What does that mean?
Due to the "completeness" property, it is possible to know the number of nodes at each level, except for the last one. Let's visualise this with an example:
heap = [9, 17, 13, 21, 23, 15, 17]
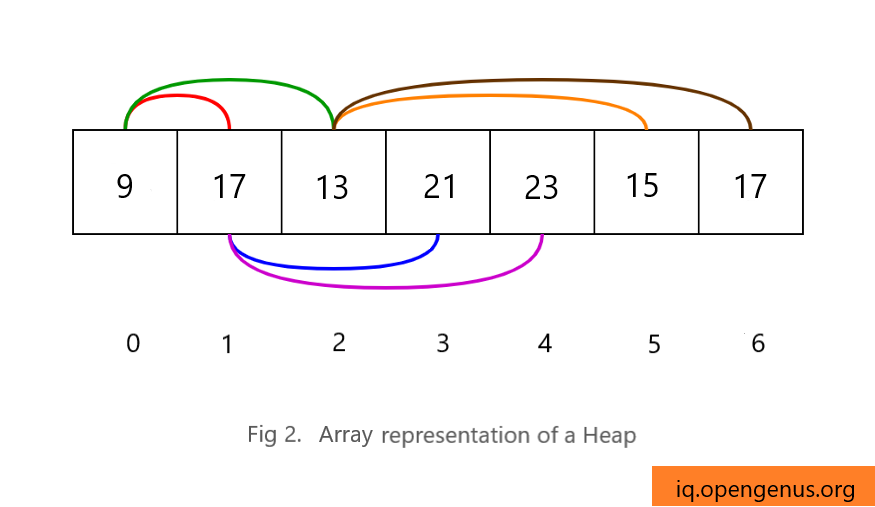
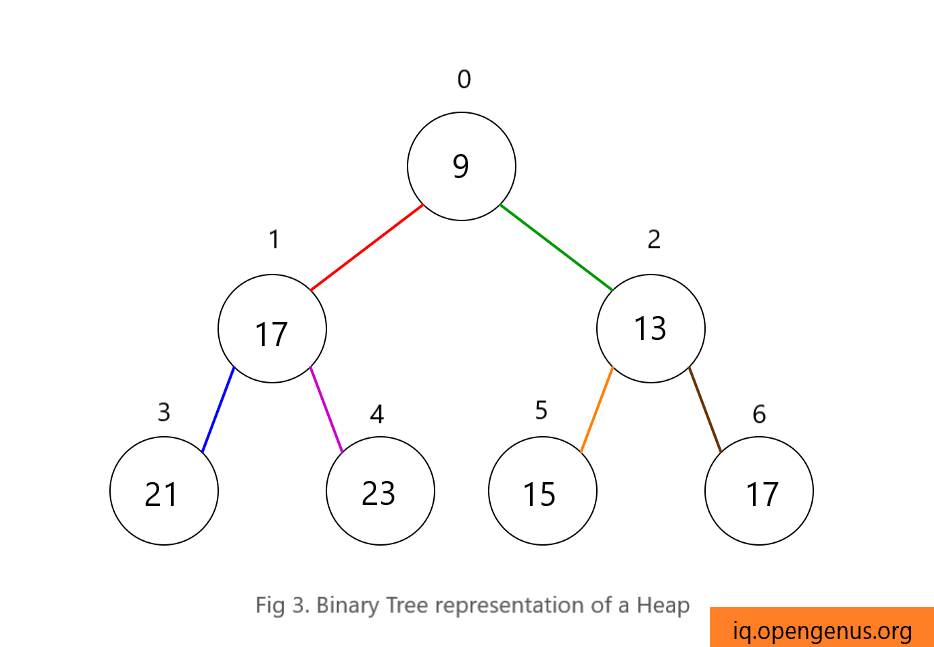
You can see from Fig 2 and Fig 3, how a heap is implemented using a Python list.
This implementation differs from the textbook heap algorithms in two aspects:
(a) Zero-based indexing
(b) "Min heap" is used instead of "Max heap".
Mathematically,
heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]
for all k, counting elements from zero. For the sake of comparison, non-existing elements are considered to be infinite.
You can create a heap in two different ways:
- Initialize a list to [], and the add elements to it using
heappush(). - Transform a populated list using
heapify().
Example:
>>> import heapq
>>> # Initialising an empty list and adding elements one by one
>>> heap = []
>>> heapq.heappush(heap, 5)
>>> heapq.heappush(heap, 2)
>>> heapq.heappush(heap, 9)
>>> heap
[2, 5, 9]
>>> # Using a populated list
>>> heap = [5, 2, 9]
>>> heapq.heapify(heap)
>>> heap
[2, 5, 9]
Heapq functions
Let us now explore the fuctions provided by this module.
>>> import heapq as heapq
>>> method_list = [func for func in dir(hq) if callable(getattr(hq, func)) and not func.startswith(("__", "_"))]
>>> method_list
['heapify', 'heappop', 'heappush', 'heappushpop', 'heapreplace', 'merge', 'nlargest', 'nsmallest']
- heapify()
It transforms a list into a heap. This tranformation happens in-place, i.e., the original list itself is modified, which happens in linear time.
Syntax:
heapq.heapify(list)
Example:
>>> import heapq as hq
>>> heap = [5, 7, 1, 22, 9, 13, 12]
>>> hq.heapify(heap)
>>> heap
[1, 7, 5, 22, 9, 13, 12]
Although, the list is not sorted, you can check that it still follows the min heap property.
- heappop()
It removes and returns (pops) the smallest item from the heap, i.e., heap[0]. Moreover, it ensures that heap[0] is replaced by the next smallest element and keeps the heap invariant. If the heap is empty, IndexError is raised.
Syntax:
heapq.heappop(heap)
Example:
>>> heap = []
>>> # Raises IndexError if empty heap is passed
>>> hq.heappop(heap)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
IndexError: index out of range
>>> heap = [9, 17, 13, 21, 23, 15, 17]
>>> hq.heappop(heap)
9
>>> heap
[13, 17, 15, 21, 23, 17]
Notice after using heappop(), how the orders of other elements is changed. This happens to keep the heap invariant, i.e., to preserve the min heap property.
- heappush()
It adds an item to a heap, maintaining the heap invariant. It is suggested not to use this function for any list, but only for those lists built using heapq functions.
Syntax:
heapq.heappush(heap, item)
Example:
>>> import heapq as hq
>>> heap = []
>>> items_to_add = (2, 3, 4, 1, 10, 8, 2, 20, 15)
>>> for item in items_to_add:
... hq.heappush(heap, item)
...
>>> heap
[1, 2, 2, 3, 10, 8, 4, 20, 15]
>>> # Add one more item to heap using heappush()
>>> hq.heappush(heap, -1)
>>> heap
[-1, 1, 2, 3, 2, 8, 4, 20, 15, 10]
- heappushpop()
It first adds the given item to the heap, then removes and return the smallest item from the heap. This is equivalent to using heappush() and then a separate call to heappop(), but is more efficient than using the two operations separately.
Syntax:
heapq.heappushpop(heap, item)
Example:
>>> # Using the heap from previous example
>>> heap
[-1, 1, 2, 3, 2, 8, 4, 20, 15, 10]
>>> hq.heappushpop(heap, 0)
-1
>>> heap
[0, 1, 2, 3, 2, 8, 4, 20, 15, 10]
- heapreplace()
It removes and return the smallest item from the heap, and also push the new item. The heap size doesn’t change. If the heap is empty, IndexError is raised. This is equivalent to using heappop() and then a separate call to heappush(), but is more efficient than using the two operations separately.
It is more appropriate to use this function when dealing with fixed-size heap.
Syntax:
heapq.heapreplace(heap, item)
Example:
>>> # Using the heap from previous example
>>> heap
[0, 1, 2, 3, 2, 8, 4, 20, 15, 10]
>>> hq.heapreplace(heap, -2)
0
>>> heap
[-2, 1, 2, 3, 2, 8, 4, 20, 15, 10]
The next three functions of this module is geaneral purpose functions based on heaps.
- merge()
It merges multiple sorted inputs into a single sorted output and returns an iterator. It does not pull the data into memory all at once, and assumes that each of the input streams is alread sorted.
It has two optional arguments:
- key - specifies a key function on how the comparison should be made between the elements. Default is
None. - reverse - it is a boolean value, and if set to
True, then the input elements are merged in reverse order, i.e., from largest to smallest. Default isFalse.
Syntax:
heapq.merge(*iterables, key=None, reverse=False)
One of the application of this function is to implement an email scheduler.
Suppose we want to send one kind email every 10 minutes, and other every 15 minutes. Below is the implementation on how we can merge these two schedules.
import datetime as dt
import heapq as hq
def email(frequency, subject):
current = dt.datetime.now()
while True:
current += frequency
yield current, subject
fast_email = email(dt.timedelta(minutes=10), "fast email")
slow_email = email(dt.timedelta(minutes=15), "slow email")
merged = hq.merge(fast_email, slow_email)
print(f"Current time: {dt.datetime.now()} \n")
for _ in range(10):
print(next(merged))
It gives the following output:
Current time: 2020-11-17 17:26:43.456526
(datetime.datetime(2020, 11, 17, 17, 36, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 17, 41, 43, 456526), 'slow email')
(datetime.datetime(2020, 11, 17, 17, 46, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 17, 56, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 17, 56, 43, 456526), 'slow email')
(datetime.datetime(2020, 11, 17, 18, 6, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 18, 11, 43, 456526), 'slow email')
(datetime.datetime(2020, 11, 17, 18, 16, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 18, 26, 43, 456526), 'fast email')
(datetime.datetime(2020, 11, 17, 18, 26, 43, 456526), 'slow email')
Here, both the inputs of the merge() functions are infinite iterators. Notice the current time and the scheduled time of the emails. The emails are arranged according to their timestamps.
- nlargest()
It returns a list of the n largest elements from the dataset defined by the iterable. This iterable doesn't need to satisfy the properties of a heap.
It has one optional keyword argument:
- key - specifies a key function on how the comparison should be made between the elements. Default is
None.
Syntax:
heapq.nlargest(n, iterable, key=None)
Example:
The following dataset is taken from Heptathlon (Women) Event - Rio 2016 Summer Olympics. Heptathlon is combined athletic event made up of seven events. Scoring is done for each event and person with the highest score is termed as winner.
>>> result = '''\
... Brianne THEISEN EATON (CAN) 6653
... Jessica ENNIS HILL (GBR) 6775
... Nafissatou THIAM (BEL) 6810
... Gyorgyi ZSIVOCZKY-FARKAS (HUN) 6442
... Laura IKAUNIECE-ADMIDINA (LAT) 6617
... Carolin SCHÄFER (GER) 6540
... Katarina JOHNSON-THOMPSON (GBR) 6523
... Yorgelis RODRIGUEZ (CUB) 6481
... Anouk VETTER (NED) 6394
... Jennifer OESER (GER) 6401
... '''
>>>
>>> import heapq as hq
>>> top_3 = hq.nlargest(
... 3, result.splitlines(), key=lambda x: float(x.split()[-1])
... )
>>>
>>> print("\n".join(top_3))
Nafissatou THIAM (BEL) 6810
Jessica ENNIS HILL (GBR) 6775
Brianne THEISEN EATON (CAN) 6653
result is a string in which individual data in separated by newline. result.splitlines() converted this string into a list of strings where each element consists of athlete name and score, separated by tabs. Now, the key function specifies to use the floating point score for comparison.
- nsmallest()
This function has similar parameters as nlargest() function, but returns n largest elements.
Syntax:
heapq.nsmallest(n, iterable, key=None)
Note: The last two functions, nlargest() and nsmallest(), performs best for smaller values of n. For larger values, it is more efficient to use sorted() function. Also, when only min or max element is needed, i.e. for n=1, using built-in min() or max() functions is suggested. Also, if repeated usage of these functions is required, it is more efficient to convert the iterable into an actual heap.
Applications of heapq module
- Implementing schedulers, as shown in one of the emaxples above.
- Implementing priority queues.
- It also has several other usage in areas like Artificial Intelligence (AI), Machine Learning (ML), etc.
- Some optimization problems.
Exercise:
It is highly recommended to try these problems yourselves before consulting the solution.
- Implement heapsort algorithm.
Solution:
import heapq as hq
def heapsort(iterable):
heap = []
for item in iterable:
hq.heappush(heap, item)
return [hq.heappop(heap) for i in range(len(heap))]