Huffman Encoding [explained with example and code]
We have explored Huffman Encoding which is a greedy algorithm that encodes a message into binary form efficiently in terms of space. It is one of the most successful Encoding Algorithms. We have present a step by step example of Huffman Encoding along with C++ implementation.
Table of content:
- Basics of Encoding
- Introduction to Huffman Encoding
- Steps to build Huffman Tree
- Psuedocode of Huffman Encoding
- Step by Step example of Huffman Encoding
- Print codes from Huffman Tree
- Implementation of Huffman Code using C++ STL
- Time and Space Complexity of Huffman Encoding
We will dive into Huffman Encoding directly now.
Basics of Encoding
First of all, let us understand What is "Encoding"?
Encoding means to convert the text in some other format.We generally perform encoding for reducing the size of the file.Suppose a text file is available then we can convert the text file in some other format which might be taking less space i.e. we can convert each character in the file in the form of binary string. Converting in the form of binary string would be beneficial because to store a binary 0 or 1 we need only one bit but to store a character we need 8 bits.
Loseless Compression reduces a file's size with no loss of quality. For loseless compression, we rewrite the data of the original file in a more efficient way mostly in the form of binay string. For compression, a table representing the frequency of each character in a file is being built. Using table an optimal way for representing each character as a binary string is being determined.
There are two types of encoding:
- Fixed-Length Encoding : In this method,each character is represented by a fixed length binary codes.
- Variable-Length Encoding : In this method,each character is represented by a variable length binary codes.
Both the encoding techniques would definetly reduce the size of the file but Variable-Length encoding is better than Fixed-Length encoding.Let's understand this with an example.Suppose there is a file for which we have created a table representing the frequency of each character as follows:
a=45
b=11
c=6
d=16
e=100
f=50
"Fixed-Length Encoding"
Fixed-Length Encoding means assigning each character binary codes of fixed length.Since there are 6 characters so we need 3 bits to store each character uniquely.So,total bits required to store the whole file is 3.(45+11+6+16+100+50) = 684 bits.
"Variable-Length Encoding"
Since in this method each character is being assigned variable length binary codes so what we try to do here is to assign frequent characters short code words and unfrequent characters long code words.Consider the scheme:
a=10,b=100,c=101,d=110,e=1,f=11
In this case,total bits required to store the whole file is (45.2+11.3+6.3+16.3+100.1+50.2) = 389 bits.
One can easily see the difference between the spaces required to store a file using
Fixed-Length Encoding and Variable-Length Encoding.So,we can conclude that Variable-Length Encoding is much better.After having enough insight about encoding let's now learn about Huffman Encoding.
Introduction to Huffman Encoding
Huffman Encoding is a famous greedy algorithm that is used for the loseless compression of file/data.It uses variable length encoding where variable length codes are assigned to all the characters depending on how frequently they occur in the given text.The character which occurs most frequently gets the smallest code and the character which occurs least frequently gets the largest code.
Till now we have seen how we can easily compress the file using encoding but we haven't thought what if we want to regenerate the original file from the encoded one.For that we need to ensure one more thing that the codewords assign to a character should not be the prefix of any other codeword.Such codes are called as "Prefix Codes".There comes a question in mind why do we need prefix codes for compression of a file.Let's understand this with an example.Consider the variable-length code schemes as follows:
a=0,b=010,c=01,d=10
A segment of encoded message such as '00101001'can be decoded in more than than one way.This can be interpreted in atleast two ways:
1.'0 0 10 10 01' ->aaddc
2.'0 010 10 01' ->abdc
This is the problem with Variable-Length encoding i.e. we are not able to decode the message/text uniquely.To make decoding efficient we need to insure that codes assigned to each character must be prefix codes.
Prefix Codes
How to generate Prefix Codes?
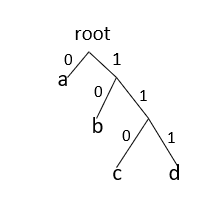
For obtaining Prefix Codes we can associate each codeword with the nodes of the binary tree.Each left branch is marked as 0 and each right branch is marked as 1 in the binary tree.During decoding,each codeword can be obtained by collecting all the 0s and 1s from the root to each leaf.Every time a leaf is reached we know that is the end of the codeword.See the fig.
There are two major parts in Huffman Encoding:
1.Build a huffman tree from input characters.
2.Traverse the huffman tree and assign codes to characters.
Steps to build Huffman Tree
Input is an array of unique characters along with their frequency of occurrences and output is Huffman Tree.
Data Structure Involved:
- Priority Queue : Priority Queue is a data structure where every item has a priority associated with it and an element with high priority is dequeued before an element with low priority.It can be implemented using binary heap.
Binary heap can be either minheap or maxheap. In minheap,the tree is complete and the item at root must be minimum among all the items present in heap.This is recursively true for all the other nodes in the binary tree.Similarly in max heap the item at root must be maximum among all the items present in heap.Here we are going to use minheap implementation of Priority Queue.
By default, C++ creates a maxheap for priority queue.
Syntax : priority_queue<datatype> name_of_priority_queue
Minheap for priority queue
Syntax : priority_queue<datatype,vector<datatype>,compare>name_of_priority_queue
Compare is a function which helps user to decide the priority according to which element should be arranged in the queue.In the Huffman encoding implementation,according to frequency element would be arranged in the queue.Element having least frequency would be at the root of the heap.
Methods supported by priority_queue:
- priority_queue::push() -> This function adds the element at the end of the queue and then elements arrange themselves according to the priority.
- priority_queue::top() -> Returns a reference to the top most element of the queue.
- priority_queue::pop() -> Deletes the first element of the queue and then elements arrange themselves according to the priority.
Steps for Huffman Encoding:
- Create a leaf node for every character in the input. Build a Minimum Heap of all leaf nodes.
- For the Minimum Heap, get the top two nodes (say N1 and N2) with minimum frequency.
- Create a new internal node N3 with frequency equal to the sum of frequency of nodes N1 and N2. Make N1 as the left child of N3 and N2 as the right child of N3. Add this new node N3 to the Minimum Heap.
- Repeat steps 2 and 3 till the point, the Minimum Heap has only one node.
Psuedocode of Huffman Encoding
Psuedocode of Huffman Encoding:
void HuffmanCodes(char data[],int freq[],int size){
//In minheap we will store a MinHeapNode which contains two variables data and frequency.Data represents the character.Also there exist two pointers left and right which is storing the address of the node which is at the left of and at the right of the given node.
struct MinHeapNode *left,*right,*top;
//create a min heap using STL.compare function is ensuring that element should be arranged according to frequency in the minheap.
priority_queue<MinHeapNode*,vector<MinHeapNode*>,compare> minheap;
// For each character create a leaf node and insert each leaf node in the heap.
for(int i=0;i<size;i++){
minheap.push(new MinHeapNode(data[i],freq[i]));
}
//Iterate while size of min heap doesn't become 1
while(minheap.size()!=1){
//Extract two nodes from the heap.
left = minheap.top();
minheap.pop();
right = minheap.top();
minheap.pop();
//Create a new internal node having frequency equal to the sum of
two extracted nodes.Assign '$' to this node and make the two extracted
node as left and right children of this new node.Add this node to the
heap.
tmp = new MinHeapNode('$',left->freq+right->freq);
tmp->left = left;
tmp->right = right;
minheap.push(tmp);
}
}
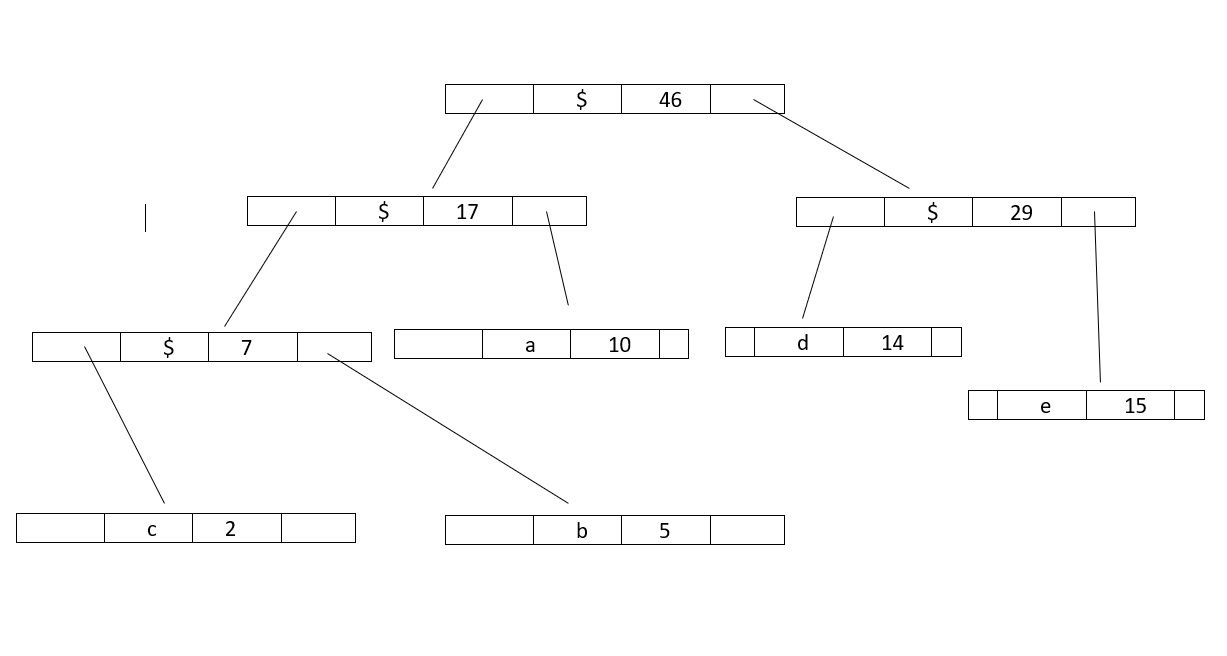
Step by Step example of Huffman Encoding
Let's understand the above code with an example:
Character :: Frequency
a :: 10
b :: 5
c :: 2
d :: 14
e :: 15
Step 1 : Build a min heap containing 5 nodes.
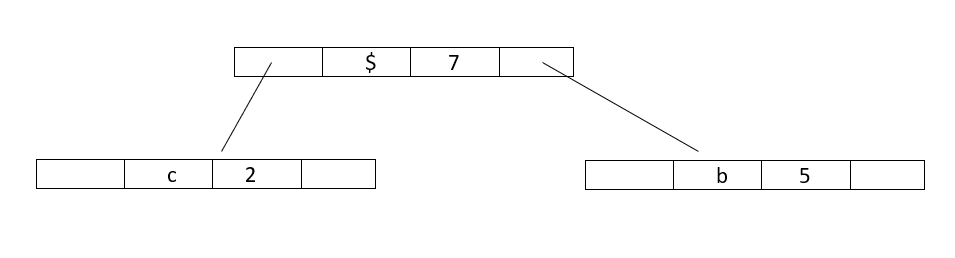
Step 2 : Extract two minimum frequency nodes from min heap.Add a new internal node 1 with frequency equal to 5+2 = 7
Now minheap contains 4 nodes:
Character :: Frequency
a :: 10
Internalnode1 :: 7
d :: 14
e :: 15
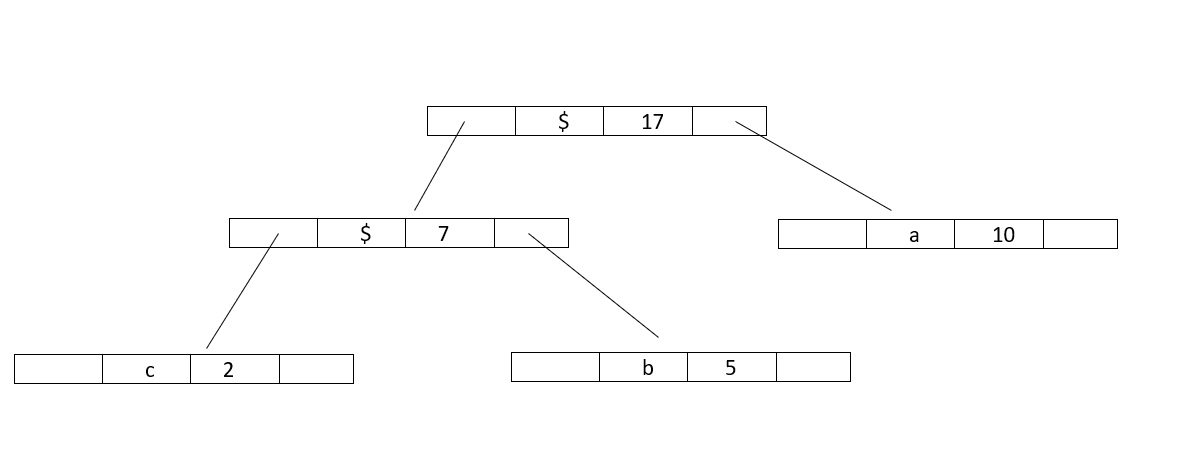
Step 3 : Again,Extract two minimum frequency nodes from min heap and add a new internal node 2 with frequency equal to 7+10 = 17
Now minheap contains 3 nodes:
Character :: Frequency
Internalnode2 :: 17
d :: 14
e :: 15
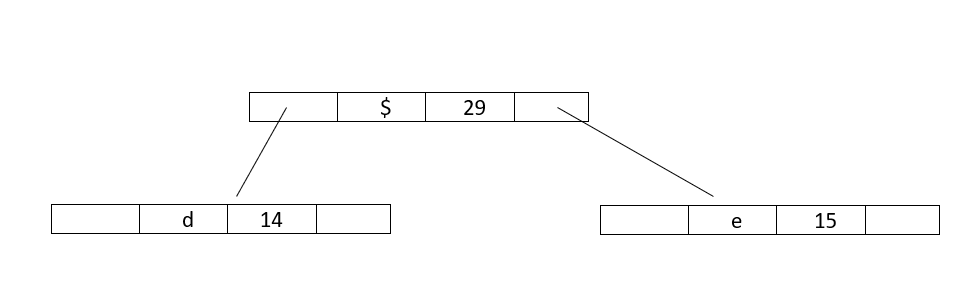
Step 4 : Extract two minimum frequency nodes from min heap and add a new internal node 3 with frequency equal to 15+14 = 29
Now minheap contains 2 nodes:
Character :: Frequency
Internalnode2 :: 17
Internalnode3 :: 29
Step 5 : Extract two minimum frequency nodes from min heap and add a new internal node 4 with frequency equal to 17+29 = 46
Now minheap contains 1 node:
Character :: Frequency
Internalnode4 :: 46
Since the heap contains only one node so, the algorithm stops here.Thus,the result is a Huffman Tree.
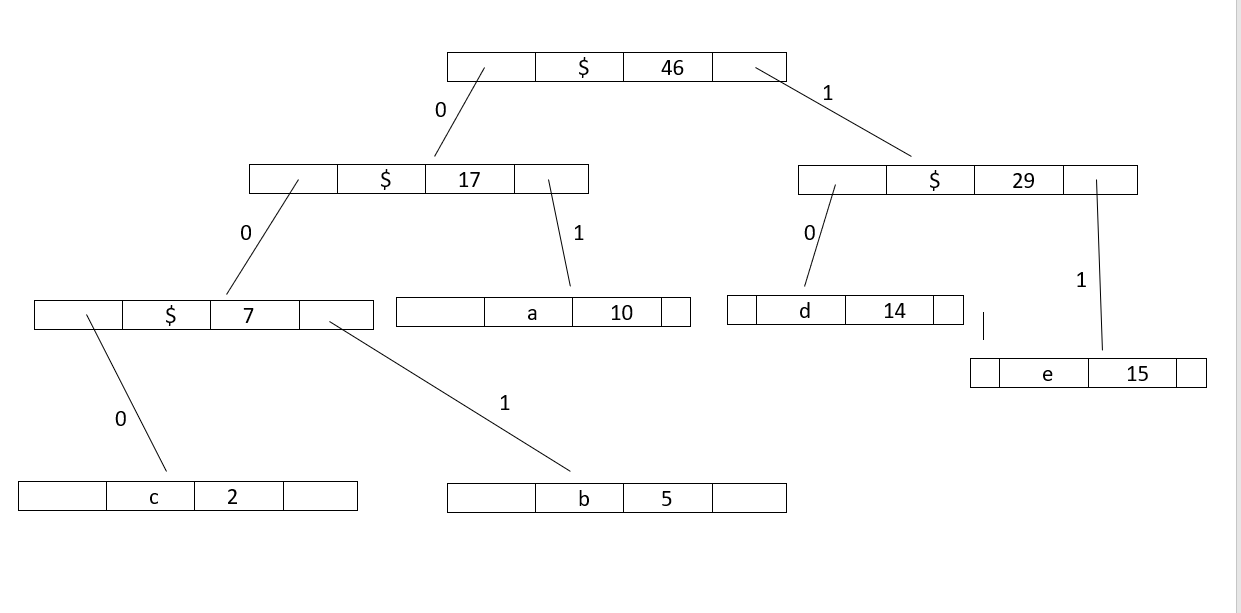
Print codes from Huffman Tree
The steps to Print codes from Huffman Tree:
- Traverse the tree formed starting from the root.
- Maintain a string.
- While moving to the left child write '0' to the string.
- While moving to the right child write '1' to the string.
- Print the string when the leaf node is encountered.
Psuedocode
void printCodes(struct MinHeapNode* root,string str){
//If root is Null then return.
if(!root){
return;
}
//If the node's data is not '$' that means it's not an internal node and print the string.
if(root->data!='$'){
cout<<root->data<<": "<<str<<endl;
}
printCodes(root->left,str+"0");
printCodes(root->right,str+"1");
}
For the above example codes are:
a: 01
b: 001
c: 000
d: 10
e: 11
Implementation of Huffman Code using C++ STL
Implementation of Huffman Code using STL:
#include<bits/stdc++.h>
using namespace std;
//Huffman tree node
struct MinHeapNode{
char data;
int freq;
MinHeapNode *left,*right;
MinHeapNode(char data,int freq){
left=right=NULL;
this->data=data;
this->freq=freq;
}
};
//For comparison of two nodes.
struct compare{
bool operator()(MinHeapNode *l,MinHeapNode *r)
{
return (l->freq>r->freq);
}
};
//Print Huffman Codes
void printCodes(struct MinHeapNode* root,string str){
//If root is Null then return.
if(!root){
return;
}
//If the node's data is not '$' that means it's not an internal node and print the string.
if(root->data!='$'){
cout<<root->data<<": "<<str<<endl;
}
printCodes(root->left,str+"0");
printCodes(root->right,str+"1");
}
//Build Huffman Tree
void HuffmanCodes(char data[],int freq[],int size){
struct MinHeapNode *left,*right,*top;
//create a min heap.
priority_queue<MinHeapNode*,vector<MinHeapNode*>,compare> minheap;
// For each character create a leaf node and insert each leaf node in the heap.
for(int i=0;i<size;i++){
minheap.push(new MinHeapNode(data[i],freq[i]));
}
//Iterate while size of min heap doesn't become 1
while(minheap.size()!=1){
//Extract two nodes from the heap.
left = minheap.top();
minheap.pop();
right = minheap.top();
minheap.pop();
//Create a new internal node having frequency equal to the sum of
two extracted nodes.Assign '$' to this node and make the two extracted
node as left and right children of this new node.Add this node to the
heap.
tmp = new MinHeapNode('$',left->freq+right->freq);
tmp->left = left;
tmp->right = right;
minheap.push(tmp);
}
//Calling function to print the codes.
printCodes(minheap.top()," ");
}
int main(){
char arr[] = {'a','b','c','d','e'};
int freq[] = {10,5,2,14,15};
int size=5;
HuffmanCodes(arr,freq,size);
return 0;
}
Output :
c: 000
b: 001
a: 01
d: 10
e: 11
Time and Space Complexity of Huffman Encoding
Time Complexity : O(nlogn),where n is the number of unique characters.
Time Complexity is O(nlogn) because we are extracting minimum nodes 2*(n-1) times and each time whenever a node is being extracted from the heap then a function called heapify() is being called to rearrange the element according to their priority.This function heapify() takes O(logn) time.
Space Complexity: O(N)
Question
Consider a file containing 6 unique characters and frequency of each character is given:
c=34
d=9
g=35
u=2
m=2
a=100
How many bits are required to store this file using Huffman Encoding?Also decode the text "0101101101001"
Options are:
- 324 ,dacm
- 328 ,dacm
- 328 ,cgam
- 390 ,dacu
With this article at OpenGenus, you must have the complete idea of Huffman Encoding. Can you decode a message encoded by Huffman Encoding Algorithm? Try it.