Understand Naive Bayes Classifier with example

Naive Bayes Classifier is a Classification algorithm belonging to the family of "probablistic classifiers".

Imagine that you have 2 sets of emails,each of them cassified into "spam mail" and "not spam" mail. Now,you receive the content of a new email,and you have to predic whether it's spam or not.Since the text data would be pretty big,we need to classify it correctly with the least possible time complexity.

In this algorithm,what we mainly do is calculate probability of occurunce of ceratin features and label based on those probabilities.
For eg:In the spam filtering problem,If many words that are present commonly in spam mails is also present in the mail that we need to classify,then this mail has a higher "chance"(probability) of being a spam mail.

In this article we will disciss how this is done.

As the name implies,Naive Bayes Classifier is based on the bayes theorem.
This algorithm works really well when there is only a little or when there is no dependency between the features.

According to the bayes theorem,

P(A/B)=( P(B/A) * P(A) )/ ( P(B) ) 

Here

P(A/B) is a conditional probability: the likelihood of event occurring given that is true.

P(B/A) is also a conditional probability: the likelihood of event occurring given that is true.

P(A) and P(B) are the probabilities of observing and independently of each other.

For the Naive Bayes algorithm we are about to explain,we will assume that the given data will be categorical for simplicity.

We will consider the following dataset and explain the algorithm as we solve a manual example.

Weather and Car are features,with these the Class is to be classified.

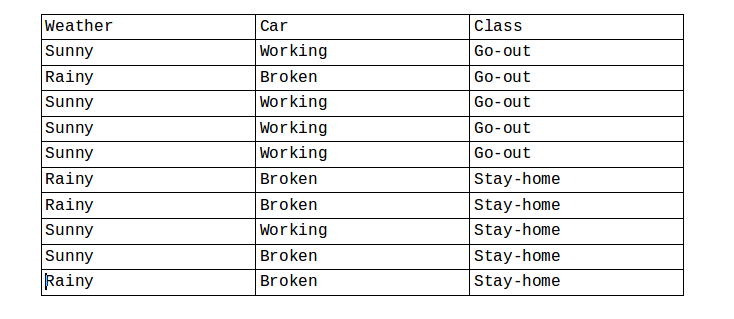
Now we will calculate basic probabilities,

P(Go-out)=Count(Go-out)/(Count(Go-out)+Count(Stayhome))
        =5/(5+5)=1/2=0.5

Similarly,

P(Stay-home)=0.5

Now, We will calculate the conditional probabilities,

For the Feature “Weather”

Note: here “and” denotes that while taking count,only the rows
where both of the categorical feature values occur together
should be counted

P (rainy|go-out)= 
        Count(“rainy” and “go-out”)/Count(go-out)

P (Sunny|go-out)= 
        Count(“Sunny” and “go-out”)/Count(go-out)


P (rainy|Stay-home)= 
        Count(“rainy” and “Stay-home”)/Count(Stay-home)

P (Sunny|go-out)= 
        Count(“Sunny” and “Stay-home”)/Count(Stay-home)

Solving these equations,we get,

P (Sunny|go-out)= 4/5 = 0.8

P (rainy|go-out)= 1/5 =0.2

P (Sunny|stay-home)= 2/5 = 0.4

P (rainy|stay-home)= 3/5 =0.6

We will do the same for the feature Car and we end up with these values,(Try solving it on your own)

P (Working|go-out)= 4/5 = 0.8

P (Broken|go-out)= 1/5 =0.2

P (Working|stay-home)= 2/5 = 0.2

P (Broken|stay-home)= 3/5 =0.8

Now since we have found all the necessary values.With these values ,we can predict the labels given an input.

We do this using the bayes theorem.

Suppose an input “Sunny”,”Working” is given.

We will find both ,

P(go-out/(Sunny and Working))=

        P(Sunny/go-out)*P(Working/go-out)*P(go-out)/(P(Sunny)*P(Working))

P(Stay-home/(Sunny and Working))=

        P(Sunny/Stay-home)*P(Working/Stay-home)*P(Stay-home)/(P(Sunny)*P(Working))

Which ever of these equations give greater value,we assign it to that label.Since the denominators are same for both the equations,to save some calculation,we will calculate only the numerator and take the maximum of them.

Now for the given input,

P(go-out/(Sunny and Working))=0.8*0.8*0.5=0.32
P(Stay-home/(Sunny and Working))=0.4*0.2*0.5=0.04

For this case since go-out>stay-home,we will assign the label go-out.If you cross-check with the dataset,we can see that the prediction is correct.

This can be done for all the input dataset,Eventhough for some cases it will give a wrong prediction.Like most machine learning algorithms this also won’t give 100% accuracy.If you solve for all values of this particular input dataset you will get an accuracy of 80% which is quite good.

Since you have a basic understanding about naive bayes,
do you think that naive bayes classifier is very much similar to k-nearest neighbours classifiers when k=size of your training set?

Applications:

Naive bayes works really works well for document classification problems,"Determining whether a given (text) document corresponds to one or more categories".
It can be used to predict text classification problems like,
i)if an e-mail is spam or not
ii)what topic an article might be reffering to
ii)who wrote an email

Here words are assumed to be independent of each other.

Following code is a python implementation of the same.

import numpy as np
from collections import defaultdict

def count_words(features,output):
    my_set=[]

    d=defaultdict(float)
    for i in range(0,len(features)):
        for j in range(0,len(features[0])):

            d[features[i][j]]=0

    for i in range(0,len(output)):
        d[output[i]]=0

    for i in range(0,len(features)):
        for j in range(0,len(features[0])):
            d[features[i][j]]=d[features[i][j]]+1

    for i in range(0,len(output)):
        d[output[i]]=d[output[i]]+1

    for i,j in enumerate(set(output)):
        for k in range(0,len(features)):
            for p,q in enumerate(set(features[k])):
                d[q+"/"+j]=0

    for i,j in enumerate(output):
        for k in range(len(features)):
            d[features[k][i]+"/"+j]=d[features[k][i]+"/"+j]+1

    return d


def calculate_probabilities(d,features,output):
    x=defaultdict(float)
    sumi=sum([d[j] for j in set(output)])
    for i in output:
        x[i]=(d[i]*1.0)/(sumi)

    for i,j in enumerate(set(output)):
        for k in range(0,len(features)):
            for p,q in enumerate(set(features[k])):
                x[q+"/"+j]=d[q+"/"+j]/d[j]

    return x

def final_prediction(x,features,output):
    predict_array=[]
    predict_array_prob=[]
    for i in range(0,len(features[0])):
        predict_array.append(0)
        predict_array_prob.append(0)

    for k in set(output):
        for i in range(0,len(features[0])):
            temp=1.0
            for j in range(0,len(features)):
                temp=temp*x[features[j][i]+"/"+k]
            if(predict_array_prob[i]<temp*x[k]):
                predict_array[i]=k
                predict_array_prob[i]=temp*x[k]

    return(predict_array)

Weather=["sunny","rainy","sunny","sunny","sunny","rainy","rainy","sunny","sunny","rainy"]
Car=["working","broken","working","working","working","broken","broken","working","broken","broken"]
Class=["go-out","go-out","go-out","go-out","go-out","stay-home","stay-home","stay-home","stay-home","stay-home"]

d=count_words([Weather,Car],Class)
x=calculate_probabilities(d,[Weather,Car],Class)
predict_array=final_prediction(x,[Weather,Car],Class)#Testing on the training set itself

for i in range(0,len(Weather)):
    print(Weather[i],"\t",Car[i],"\t-->\tprediction is ",predict_array[i])