Priority Queue in Python using OOP
Table of contents:
- Problem Statement
- Solution Description
- Implementation (Code)
- Complexity Analysis
- Question
Problem Statement
In this article at OpenGenus, we will implement priority queue in Python, utilizing Object-Oriented Programming (OOP). A priority queue is similar to a queue. However, while a queue's dequeue() and enqueue() methods follow the rule First in First out (FIFO), a priority queue will remove and return the value upon deletion based on a priority. For example, a priority queue that follows the rule "larger value, higher priority" will remove and return the largest element upon deletion. A priority queue that follows the rule "smaller value, higher priority" will remove and return the smallest element upon deletion. The priority queue that we build will allow duplicates.
Solution Description
We will implement a heap-based priority queue by using the binary heap. The BinaryHeap class will be the Superclass. The PriorityQueue class will be the Subclass of the BinaryHeap class. Whenever we want to dequeue() the priority queue, we call the delete() method of the BinaryHeap class. When we want to enqueue() priority queue, we call the insert() method of the BinaryHeap class.
If we want the priority in the priority queue to be "smaller value, higher priority", we use a min-heap-based priority queue. To create a min-heap-based priority queue, we create an instance of the PriorityQueue class and pass in the comparing mechanism for a min heap as an argument. In a min-heap, for any node m, m.parent.value ≤ m.value (min-heap property).
# For any node m in the min-heap:
# m.parent.value <= m.value
# Example:
#
# [ -10 -2 7 9 9 9 56 32 10 10 11 ]
#
# -10
# / \
# -2 7
# / \ / \
# 9 9 9 56
# / \ / \
# 32 10 10 11
If we want the priority in the priority queue to be "larger value, higher priority", we use a max-heap-based priority queue. To create a max-heap-based priority queue, we create an instance of the PriorityQueue class and pass in the comparing mechanism for a max heap as an argument. In a max-heap, for any node m, m.parent.value ≥ m.value (max-heap property).
# For any node m in the max-heap:
# m.parent.value => m.value
# Example:
# [ 80 77 33 77 18 -3 19 11 24 ]
# 80
# / \
# 77 33
# / \ / \
# 77 18 -3 19
# / \
# 11 24
We will use an array to represent the binary heap. In this array, for any element e at index i (where i is in the interval [0, n-1] and i is an integer):
- The left child of e is at index 2i+1
- The right child of e is at index 2i+2
- The parent of e is at index floor((i-1)/2)
The insert() method:
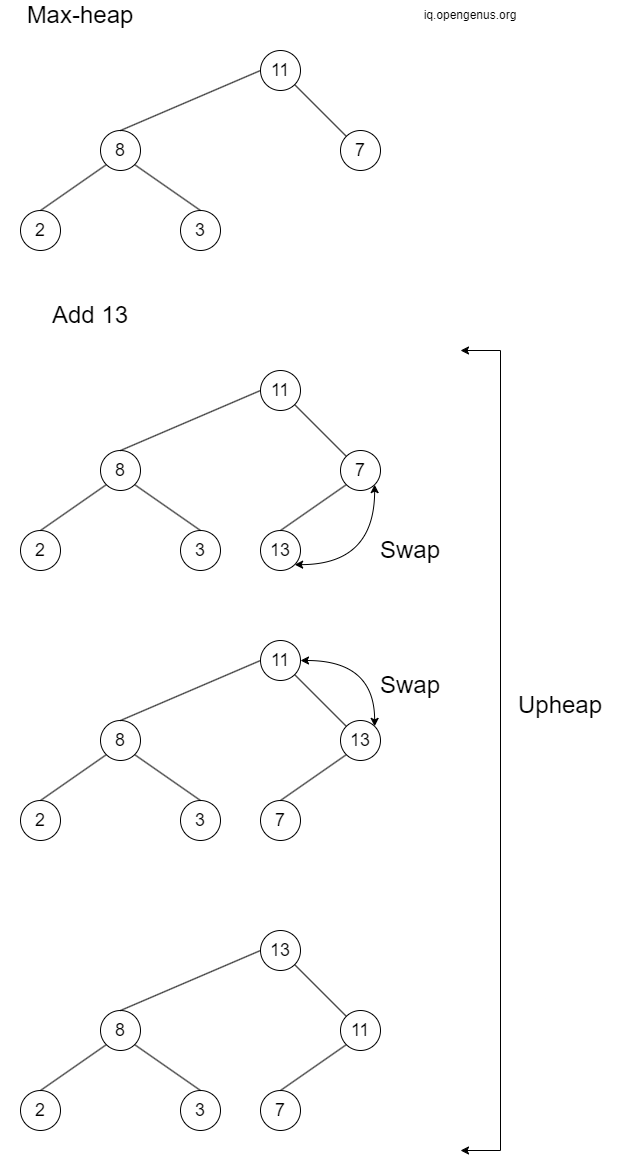
We insert() the new element to the end of the array then perform upheap to restore the heap property. (detailed implementation and example below)
The upheap() method:
We continuously compare the newly added element with its parent and perform the swap operation between that element and its parent until the heap property is restored. (detailed implementation and example below)
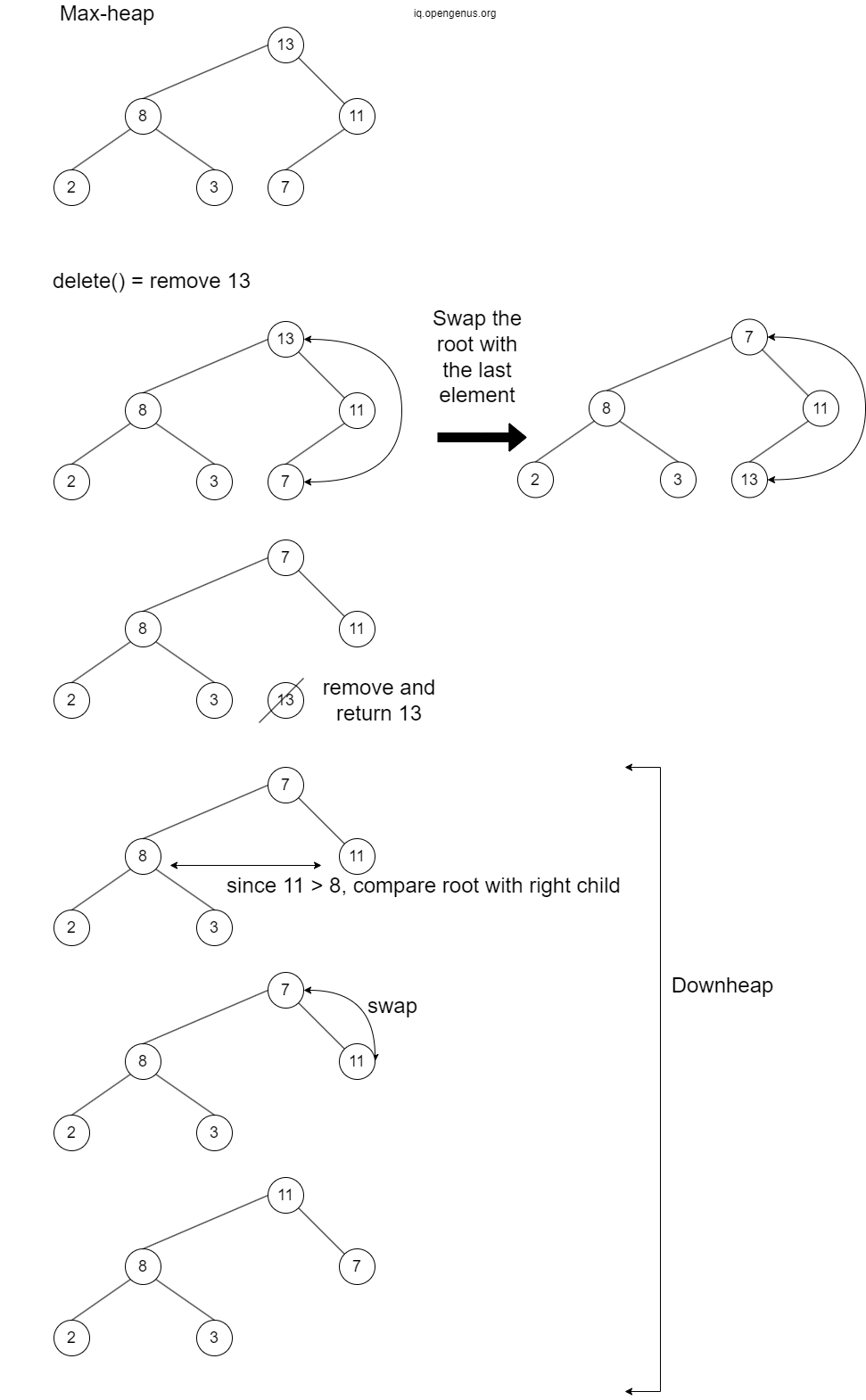
The delete() method:
We swap the root (the first element in the array) with the element at the end of the array. We then remove and return the last element in the array. Finally, we perform a down heap to restore the heap property. (detailed implementation and example below)
The downheap() method:
After we swap the root with the last element in the array and remove and return the last element in the array, we then continuously compare the current element at the root with its left and right child and swap with either its left or right child until the heap property is restored. (detailed implementation and example below)
Implementation (Code)
Node
We will first create a class called Node. This class will have 2 attributes: value and index. The attribute value is used to store the value that is inserted into the heap, and the attribute index is used to store the index of the node in the array that is used to represent the binary heap.
class Node:
value: int
index: int
def __init__(self, v, i):
self.value = v
self.index = i
BinaryHeap attributes and comparison function for min-heap and max-heap
The Superclass will be the BinaryHeap. Note that our binary heap allows duplicates. The BinaryHeap class will include 2 attributes. The first attribute is an array which is used to represent the binary heap. In this array, for any element e at index i (where i is in the interval [0, n-1] and i is an integer):
- The left child of e is at index 2*i+1
- The right child of e is at index 2*i+2
- The parent of e is at index floor((i-1)/2)
The second attribute is called compare_funct. The compare_funct attribute is an indication of whether the binary heap is a max-heap or a min-heap. This compare_funct is a comparison function that is passed in when we create the binary heap.
class BinaryHeap:
array: list # O(n) space where n is the number of elements
def __init__(self, compare_mechanism):
self.array = []
self.compare_funct = compare_mechanism
When we insert() or delete() a node from the binary heap, we will need to either upheap (if we insert) or downheap (if we delete) to restore the heap's property. In a max-heap, the heap property is for any node m, m.parent.value ≥ m.value. In a min-heap, the heap property is for any node m, m.parent.value ≤ m.value. During the upheap or downheap process, we will need to decide whether or not we should swap the parent node with the child node to restore the heap property. This is why we need different comparison functions (or compare_funct) for min-heap and max-heap.
The comparison function will compare the values that are stored in 2 nodes and return 1 if the heap property is violated and the 2 nodes need to be swapped to restore the heap property. If the heap property is not violated, it will return 0.
For the upheap process, node 1 will be the newly added node, and node 2 will be its parent. In a max-heap, if the newly added node has a value that is larger than the value that its parent holds (i.e. let the newly added node be a node called m, m.value > m.parent.value), the compare_funct will return 1 which indicate that the 2 nodes need to be swapped to restore the property for any node m, m.parent.value ≥ m.value. Similarly, in a min-heap, if the newly added node has a value that is smaller than the value that its parent holds (i.e. let the newly added be a node called m, m.value < m.parent.value), the compare_funct will return 1 which indicates that the 2 nodes need to be swapped to restore the property for any node m, m.parent.value ≤ m.value.
For the downheap process, node 1 will be either the left or the right child of the node that is just swapped with the root node in the deletion process, and node 2 will be the node that is just swapped with the root node in the deletion process. In the case of a max-heap, if the child's value is larger than the parent's value (i.e. let the child node be m, m.value > m.parent.value), the property for any node m, m.parent.value ≥ m.value is violated and the 2 nodes need to be swapped, thus compare_funct for max-heap will return 1. Similarly, in the case of a min-heap, if the child's value is smaller than the parent's value (i.e. let the child node be m, m.value < m.parent.value), the property for any node m, m.parent.value ≤ m.value is violated and the 2 nodes need to be swapped, thus compare_funct for min-heap will return 1.
Note that for convenience purposes, these 2 compare_funct functions are also used to compare the values of the left and right child during the downheap process. The right child will be node 1 and the left child will be node 2. The reason why we need to compare the right and left child during the downheap process is that we need to choose only 1 child to compare with the parent and, if heap property is violated, swap that child with the parent. In the case of a max-heap, we will need to choose the child that holds the larger value between the 2 children. The compare_funct for max-heap will return 1 if the right child holds a larger value and returns 0 if the left child holds a larger value. In the case of a min-heap, we will need to choose the child that holds the smaller value between the 2 children. The compare_funct for min-heap will return 1 if the right child holds a smaller value and returns 0 if the left child holds a smaller value.
For a max-heap, we pass in the compare_funct below:
def compare_funct_max_heap(node_1: Node, node_2: Node): # return 1 if need to swap (O(1) time)
if node_1.value > node_2.value:
return 1
return 0
For a min-heap, we pass in the compare_funct below:
def compare_funct_min_heap(node_1: Node, node_2: Node): # return 1 if need to swap (O(1) time)
if node_1.value < node_2.value:
return 1
return 0
BinaryHeap methods (insert, upheap, delete, and downheap)
When we insert a new element, we create a new node. The index of the new node will be the length of the array before the node is inserted into the array. The value of the new node will be the new element. We will append the node to the end of the array. The time complexity of this operation is O(1) amortized. We then perform upheap to restore the heap property.
def insert(self, new_element: int): # O(log(n))
node = Node(new_element, len(self.array))
self.array.append(node)
self.up_heap(node) # O(log(n))
In the upheap process, we compare the newly added node with its parent and swap if the heap property is violated. The time complexity of the upheap process is O(logn) since the maximum height of the heap is logn. For details on how compare_funct works, please refer to the part under the heading BinaryHeap attributes and comparison function for min-heap and max-heap.
Example of upheap process in a max-heap.
def up_heap(self, node: Node): # O(log(n))
while True:
parent = self.get_parent(node.index)
if parent is None:
break
if self.compare_funct(node, parent) == 1: # return 1 if need to swap
self.swap(node, parent)
else:
break
In the deletion operation, we know that the node at the root must be the one to be removed since the root node is the node that has either the largest value (in a max-heap) or the smallest value (in a min-heap). We will swap the node at the root with the last node in the heap, remove the last node, then perform downheap.
We will first call the delete_helper() method in the delete() method. The delete_helper() method will return None if the heap is empty. If there is only 1 node left in the heap, the node will be removed and no downheap operation needs to be done. If there is more than 1 node in the heap, the root node (first element in the array) and the last node (last element in the array) will be swapped, the last node is then removed and returned to the delete() method. If the returned value is not None and there is still more than 1 node in the heap after the removal, we perform downheap operation. After the downheap operation, return the removed value.
def delete(self): # O(log(n))
remove = self.delete_helper()
if (remove is not None) and (len(self.array) > 1):
# perform down heap
self.down_heap(self.array[0]) # O(log(n))
return remove
def delete_helper(self): # O(1)
if len(self.array) == 0:
return None # return None if the array is empty
if len(self.array) == 1:
remove = self.array[0]
self.array.pop() # remove the last element O(1)
return remove.value
# swap the first and the last element
self.swap(self.array[0], self.array[len(self.array) - 1])
# remove the last element
temp = self.array[len(self.array) - 1]
self.array.pop() # O(1) time
return temp.value
In the down_heap_helper() method, we will get the left and the right child of the node that just got swapped with the removed node.
If both the right and left child are None, the node is a leaf and further swap operation is not needed.
If the right child is None and the left child is not None, the left child will be used to compare and swap (if the heap property is violated) with the parent node. If the left child is None and the right child is not None, the right child will be used to compare and swap (if the heap property is violated) with the parent node.
If both the left and the right child are not None, we compare the value of the left and right child using the compare_funct that we passed in when we create the heap. This function will decide which child will be used to compare and swap (if the heap property is violated) with the parent node. For details on how compare_funct works, please refer to the part under the heading BinaryHeap attributes and comparison function for min-heap and max-heap.
The time complexity of the downheap process is O(logn) since the maximum height of the heap is logn.
Example of deletion and downheap process in a max-heap:
def down_heap(self, node: Node): # O(log(n))
while True:
if self.down_heap_helper(node) == 0:
break
def down_heap_helper(self, parent: Node): # return 1 if swap (O(1) time)
right_child = self.get_right_child(parent.index)
left_child = self.get_left_child(parent.index)
if (right_child is None) and (left_child is None):
return 0 # return 0 if no need to swap
to_swap_index = None
if (right_child is not None) and (left_child is not None):
if self.compare_funct(right_child, left_child) == 1:
to_swap_index = right_child.index
else:
to_swap_index = left_child.index
elif right_child is not None:
to_swap_index = right_child.index
elif left_child is not None:
to_swap_index = left_child.index
if self.compare_funct(self.array[to_swap_index], parent) == 1:
self.swap(parent, self.array[to_swap_index])
return 1 # return 1 if swap
return 0 # return 0 if not swap
BinaryHeap methods to get the left child, right child, and parent of a node
To calculate the index of the left child, right child, and parent of a node, we use the following rule: for any node e at index i (where i falls within the interval [0, n-1] and i is an integer):
- The left child of e is at index 2i+1
- The right child of e is at index 2i+2
- The parent of e is at index floor((i-1)/2)
If the calculated index falls within the interval [0, n-1], return the node at that calculated index, otherwise, return None.
Note that before calculating the index of the left child, right child, or parent of a node, we need to check if the heap is empty and if the index passed into the methods falls within the interval [0, n-1]. If both conditions are satisfied, we proceed to calculate the index of the left child, right child, or parent. Otherwise, we return None.
def get_left_child(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
left_child_index = 2 * index + 1
if (left_child_index >= 0) and (left_child_index < len(self.array)):
return self.array[left_child_index]
return None
def get_right_child(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
right_child_index = 2 * index + 2
if (right_child_index >= 0) and (right_child_index < len(self.array)):
return self.array[right_child_index]
return None
def get_parent(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
parent_index = math.floor(((index - 1) / 2))
if (parent_index >= 0) and (parent_index < len(self.array)):
return self.array[parent_index]
return None
BinaryHeap method to swap 2 nodes
We will create a swap() method to swap the positions of 2 nodes. The method takes 2 parameters: node1 and node2.
First, we store node1 in a temporary variable called temp_node and store the index of node2 in another temporary variable called temp_index. Then, we assign node2 to the position of node1 using node1's index and update the index attribute of node2 to be equal to the index of node1.
Finally, we assign node1 to the previous position of node2 using the temp_node variable which stores node1 and the temp_index variable which stores the previous index of node2 (i.e. the index of node2 before its position was changed). After that, we update the index attribute of node1 to be equal to temp_index variable which is equal the index of node2 before its position was changed.
def swap(self, node1: Node, node2: Node): # O(1) time
temp_node = node1
temp_index = node2.index
self.array[node1.index] = node2
self.array[node1.index].index = node1.index
self.array[temp_index] = temp_node
self.array[temp_index].index = temp_index
PriorityQueue class
We then create the PriorityQueue class as the subclass of BinaryHeap. Note that our priority queue allows duplicates. The PriorityQueue class will contain the following methods:
- is_empty(): check if the heap is empty or not; return True if the heap is empty; return False if the heap is not empty.
- size(): return the size of the heap which is also the size of the array attribute.
- enqueue(): call the insert() method of the BinaryHeap.
- dequeue(): call the delete() method of the BinaryHeap.
class PriorityQueue(BinaryHeap): # (allow duplicates)
def is_empty(self): # O(1)
if len(self.array) <= 0:
return True
return False
def size(self): # O(1)
return len(self.array)
def enqueue(self, new_element: int): # O(log(n))
self.insert(new_element)
def dequeue(self): # O(log(n))
return self.delete()
Full code implementation with example
import math
class Node:
# each node will include 2 attributes
# - value
# - index in the array
value: int
index: int
def __init__(self, v, i):
self.value = v
self.index = i
# Superclass
class BinaryHeap: # (allow duplicates)
# We use an array to represent the binary heap
# Note that for a heap of height h:
# - all levels < h are fully filled with nodes/ elements
# - on the last level which is h, the nodes/ elements are filled from left to right
# In the array, for any element e at index i (where i is in the interval [0, n-1] and i is an integer):
# - The left child of e is at index 2*i+1
# - The right child of e is at index 2*i+2
# - The parent of e is at index floor((i-1)/2)
array: list # O(n) space where n is the number of elements
def __init__(self, compare_mechanism):
self.array = []
self.compare_funct = compare_mechanism
def insert(self, new_element: int): # O(log(n))
node = Node(new_element, len(self.array))
self.array.append(node)
self.up_heap(node) # O(log(n))
def up_heap(self, node: Node): # O(log(n))
while True:
parent = self.get_parent(node.index)
if parent is None:
break
if self.compare_funct(node, parent) == 1: # return 1 if need to swap
self.swap(node, parent)
else:
break
def delete(self): # O(log(n))
remove = self.delete_helper()
if (remove is not None) and (len(self.array) > 1):
# perform down heap
self.down_heap(self.array[0]) # O(log(n))
return remove
def delete_helper(self): # O(1)
if len(self.array) == 0:
return None # return None if the array is empty
if len(self.array) == 1:
remove = self.array[0]
self.array.pop() # remove the last element O(1)
return remove.value
# swap the first and the last element
self.swap(self.array[0], self.array[len(self.array) - 1])
# remove the last element
temp = self.array[len(self.array) - 1]
self.array.pop() # O(1) time
return temp.value
def down_heap(self, node: Node): # O(log(n))
while True:
if self.down_heap_helper(node) == 0:
break
def down_heap_helper(self, parent: Node): # return 1 if need to swap (O(1) time)
right_child = self.get_right_child(parent.index)
left_child = self.get_left_child(parent.index)
if (right_child is None) and (left_child is None):
return 0 # return 0 if no need to swap
to_swap_index = None
if (right_child is not None) and (left_child is not None):
if self.compare_funct(right_child, left_child) == 1:
to_swap_index = right_child.index
else:
to_swap_index = left_child.index
elif right_child is not None:
to_swap_index = right_child.index
elif left_child is not None:
to_swap_index = left_child.index
if self.compare_funct(self.array[to_swap_index], parent) == 1:
self.swap(parent, self.array[to_swap_index])
return 1 # return 1 if swap
return 0 # return 0 if no need to swap
def swap(self, node1: Node, node2: Node): # O(1) time
temp_node = node1
temp_index = node2.index
self.array[node1.index] = node2
self.array[node1.index].index = node1.index
self.array[temp_index] = temp_node
self.array[temp_index].index = temp_index
def get_left_child(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
left_child_index = 2 * index + 1
if (left_child_index >= 0) and (left_child_index < len(self.array)):
return self.array[left_child_index]
return None
def get_left_child_value(self, index: int): # O(1) time
left_child = self.get_left_child(index)
if left_child is not None:
return left_child.value
return None
def get_right_child(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
right_child_index = 2 * index + 2
if (right_child_index >= 0) and (right_child_index < len(self.array)):
return self.array[right_child_index]
return None
def get_right_child_value(self, index: int): # O(1) time
right_child = self.get_right_child(index)
if right_child is not None:
return right_child.value
return None
def get_parent(self, index: int): # O(1) time
if (len(self.array) > 0) and ((index >= 0) and (index < len(self.array))):
parent_index = math.floor(((index - 1) / 2))
if (parent_index >= 0) and (parent_index < len(self.array)):
return self.array[parent_index]
return None
def get_parent_value(self, index: int): # O(1) time
parent = self.get_parent(index)
if parent is not None:
return parent.value
return None
def print_array(self): # O(n) time
print("[", end=" ")
for node in self.array:
print(node.value, end=" ")
print("]", end="")
# Subclass of BinaryHeap
class PriorityQueue(BinaryHeap): # (allow duplicates)
def is_empty(self): # O(1)
if len(self.array) <= 0:
return True
return False
def size(self): # O(1)
return len(self.array)
def enqueue(self, new_element: int): # O(log(n))
self.insert(new_element)
def dequeue(self): # O(log(n))
return self.delete()
def compare_funct_max_heap(node_1: Node, node_2: Node): # return 1 if need to swap (O(1) time)
if node_1.value > node_2.value:
return 1
return 0
def compare_funct_min_heap(node_1: Node, node_2: Node): # return 1 if need to swap (O(1) time)
if node_1.value < node_2.value:
return 1
return 0
def run_program():
max_heap = PriorityQueue(compare_funct_max_heap)
max_heap.insert(-10)
max_heap.insert(43)
max_heap.insert(6)
max_heap.insert(55)
max_heap.insert(49)
max_heap.insert(0)
max_heap.insert(60)
max_heap.insert(55)
max_heap.insert(22)
# remove the max element from max_heap one by one
print("initial max heap: ", end=" ")
max_heap.print_array()
print()
while True:
result = max_heap.delete()
if result is not None:
print("remove: ", result)
print("heap after remove ", result, ": ", end=" ")
max_heap.print_array()
print()
else:
break
print()
min_heap = PriorityQueue(compare_funct_min_heap)
min_heap.insert(-10)
min_heap.insert(-2)
min_heap.insert(9)
min_heap.insert(9)
min_heap.insert(9)
min_heap.insert(7)
min_heap.insert(56)
min_heap.insert(32)
min_heap.insert(10)
min_heap.insert(10)
min_heap.insert(11)
# remove the min element from the heap one by one
print("initial min heap: ", end=" ")
min_heap.print_array()
print()
while True:
result = min_heap.delete()
if result is not None:
print("remove: ", result)
print("heap after remove ", result, ": ", end=" ")
min_heap.print_array()
print()
else:
break
print()
print("insert 9 to min_heap")
min_heap.insert(9)
print("insert 0 to min_heap")
min_heap.insert(0)
print("insert -1 to min_heap")
min_heap.insert(-1)
min_heap.print_array() # [ -1 9 0 ]
print()
print("delete min element from min_heap: ", min_heap.delete())
min_heap.print_array() # [ 0 9 ]
print()
print("insert 12 to min_heap")
min_heap.insert(12)
print("insert 12 to min_heap")
min_heap.insert(12)
print("insert 12 to min_heap")
min_heap.insert(12)
min_heap.print_array() # [ 0 9 12 12 12 ]
print()
print("delete min element from min_heap: ", min_heap.delete())
print("delete min element from min_heap: ", min_heap.delete())
min_heap.print_array() # [ 12 12 12 ]
print()
print("insert -11 to min_heap")
min_heap.insert(-11)
min_heap.print_array() # [ -11 12 12 12 ]
print()
print("delete min element from min_heap: ", min_heap.delete())
print("delete min element from min_heap: ", min_heap.delete())
print("delete min element from min_heap: ", min_heap.delete())
min_heap.print_array() # [ 12 ]
print()
if __name__ == "__main__":
run_program()
Output:
initial max heap: [ 60 55 55 49 43 0 6 -10 22 ]
remove: 60
heap after remove 60 : [ 55 49 55 22 43 0 6 -10 ]
remove: 55
heap after remove 55 : [ 55 49 6 22 43 0 -10 ]
remove: 55
heap after remove 55 : [ 49 43 6 22 -10 0 ]
remove: 49
heap after remove 49 : [ 43 22 6 0 -10 ]
remove: 43
heap after remove 43 : [ 22 0 6 -10 ]
remove: 22
heap after remove 22 : [ 6 0 -10 ]
remove: 6
heap after remove 6 : [ 0 -10 ]
remove: 0
heap after remove 0 : [ -10 ]
remove: -10
heap after remove -10 : [ ]
# how the heap looks like every time we remove the max element
# [ 60 55 55 49 43 0 6 -10 22 ]
# 60
# / \
# 55 55
# / \ / \
# 49 43 0 6
# / \
# -10 22
# [ 55 49 55 22 43 0 6 -10 ]
# 55
# / \
# 49 55
# / \ / \
# 22 43 0 6
# /
# -10
# [ 55 49 6 22 43 0 -10 ]
# 55
# / \
# 49 6
# / \ / \
# 22 43 0 -10
# [ 49 43 6 22 -10 0 ]
# 49
# / \
# 43 6
# / \ /
# 22 -10 0
# [ 43 22 6 0 -10 ]
# 43
# / \
# 22 6
# / \
# 0 -10
# [ 22 0 6 -10 ]
# 22
# / \
# 0 6
# /
# -10
# [ 6 0 -10 ]
# 6
# / \
# 0 -10
# [ 0 -10 ]
# 0
# /
# -10
# [ -10 ]
# -10
# [ ]
initial min heap: [ -10 -2 7 9 9 9 56 32 10 10 11 ]
remove: -10
heap after remove -10 : [ -2 9 7 10 9 9 56 32 11 10 ]
remove: -2
heap after remove -2 : [ 7 9 9 10 9 10 56 32 11 ]
remove: 7
heap after remove 7 : [ 9 9 9 10 11 10 56 32 ]
remove: 9
heap after remove 9 : [ 9 10 9 32 11 10 56 ]
remove: 9
heap after remove 9 : [ 9 10 10 32 11 56 ]
remove: 9
heap after remove 9 : [ 10 11 10 32 56 ]
remove: 10
heap after remove 10 : [ 10 11 56 32 ]
remove: 10
heap after remove 10 : [ 11 32 56 ]
remove: 11
heap after remove 11 : [ 32 56 ]
remove: 32
heap after remove 32 : [ 56 ]
remove: 56
heap after remove 56 : [ ]
# how the heap looks like every time we remove the min element
# [ -10 -2 7 9 9 9 56 32 10 10 11 ]
# -10
# / \
# -2 7
# / \ / \
# 9 9 9 56
# / \ / \
# 32 10 10 11
# [ -2 9 7 10 9 9 56 32 11 10 ]
# -2
# / \
# 9 7
# / \ / \
# 10 9 9 56
# / \ /
# 32 11 10
# [ 7 9 9 10 9 10 56 32 11 ]
# 7
# / \
# 9 9
# / \ / \
# 10 9 10 56
# / \
# 32 11
# [ 9 9 9 10 11 10 56 32 ]
# 9
# / \
# 9 9
# / \ / \
# 10 11 10 56
# /
# 32
# [ 9 10 9 32 11 10 56 ]
# 9
# / \
# 10 9
# / \ / \
# 32 11 10 56
# [ 9 10 10 32 11 56 ]
# 9
# / \
# 10 10
# / \ /
# 32 11 56
# [ 10 11 10 32 56 ]
# 10
# / \
# 11 10
# / \
# 32 56
# [ 10 11 56 32 ]
# 10
# / \
# 11 56
# /
# 32
# [ 11 32 56 ]
# 11
# / \
# 32 56
# [ 32 56 ]
# 32
# /
# 56
# [ 56 ]
# 56
# [ ]
insert 9 to min_heap
insert 0 to min_heap
insert -1 to min_heap
[ -1 9 0 ]
# -1
# / \
# 9 0
delete min element from min_heap: -1
[ 0 9 ]
# 0
# /
# 9
insert 12 to min_heap
insert 12 to min_heap
insert 12 to min_heap
[ 0 9 12 12 12 ]
# 0
# / \
# 9 12
# / \
# 12 12
delete min element from min_heap: 0
delete min element from min_heap: 9
[ 12 12 12 ]
# 12
# / \
# 12 12
insert -11 to min_heap
[ -11 12 12 12 ]
# -11
# / \
# 12 12
# /
# 12
delete min element from min_heap: -11
delete min element from min_heap: 12
delete min element from min_heap: 12
[ 12 ]
# 12
Complexity Analysis
Time complexity:
- enqueue() and dequeue():
O(logn)(since upheap() and downheap() takesO(logn)) - size(), is_empty():
O(1)
Space complexity: O(n)
Question
What is the time complexity for the enqueue() operation of a heap-based priority queue?