In this article, we have explained Pumping Lemma for Regular Languages along with an intuitive proof and formal proof. This is an important result / theorem in Theory of Computation.

Table of contents:

1. Pumping Lemma for Regular Languages
2. Proof of Pumping Lemma for Regular Languages

Let us get started with Pumping Lemma for Regular Languages (with proof).

Pumping Lemma for Regular Languages

The theorem of Pumping Lemma for Regular Languages is as follows:

Given a regular language L.
There exists an integer p (pumping length) >= 1 such that for every string STR in L with length of STR >= p can be written as STR = XYZ provided:

1. y is not null / empty string
2. length of xy <= p
3. for all i >= 0, xyⁱz is a part of L.

In simple terms, a string STR in L can be written in such a form that there are three components (xyz) and if we repeat the middle portion any number of times, the resultant string is also in L.

The name follows from the idea that the middle part of the string is pumped multiple times to form the resultant string.

If this holds true for all string in L, then L is a regular language. Therefore, Pumping Lemma for Regular Languages can be used to find if a given string is in a regular language L and if a given language L is a regular language or not.

Proof of Pumping Lemma for Regular Languages

Intuitive proof:

If a string STR is long to create a cycle in Deterministic Finite Automata (DFA) for a given regular language L, then we can repeat the cycle (pump) any number of times and form infinite set of strings that will be a part of L as it is represented using the same DFA.

Formal proof:

Let Σ be the alphabet of regular language L. There exists a DFA M = (Q, Σ, δ, q, F) that accepts L. We define p (pumping length) to be the number of states in Q.

Let string STR = s₁s₂ ... s_n such that n >= p.

Let a starting state be r1.

If we take s1 as input at state r1, we move to state r2.

Therefore, if we take s_i as input at state r_i, we move to state r_i+1.

The last / final state is r_n+1.

Number of states in DFA M is p and as n >= p, by pigeonhole principle, we know that there must be a state that repeats itself.

Therefore, there exist i and j such that r_i = r_j.

Therefore, reading characters in a string y will move from state r_i to r_j. Consider the following image to visual DFA M easily.

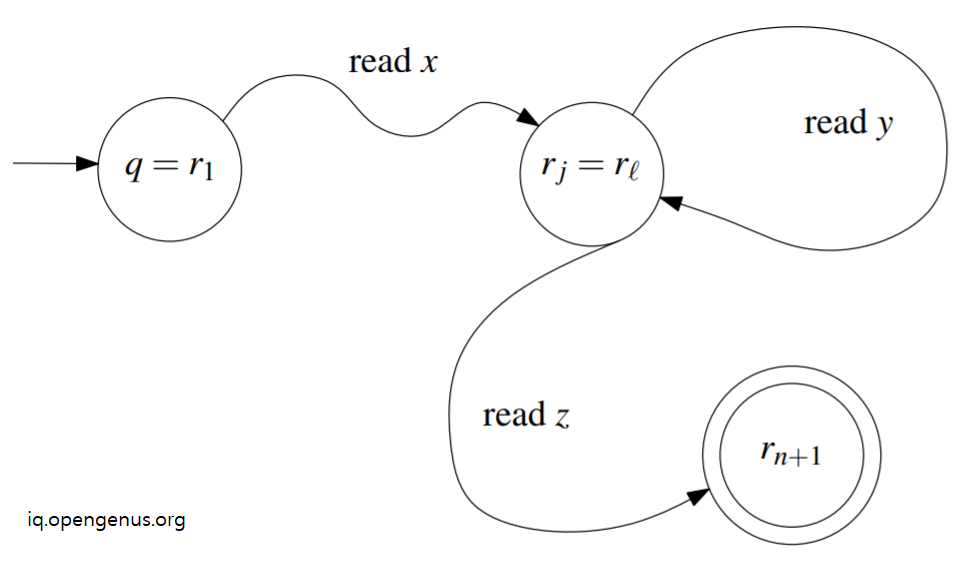
In this view, the string y can be pumped any number of times and the resultant string will stay in DFA M that is in regular language L.

With this article at OpenGenus, you must have the complete idea of Pumping Lemma for Regular Languages (with proof).