We have explained everything about Recursion in Programming along with types of Recursion, How memory is allocated to different function calls in recursion? and if Recursion should be used.

Table of content:

1. Basics of Recursion
2. Types of Recursion
3. How memory is allocated to different function calls in recursion?
4. Is recursion good in programming?

We will get started with Recursion now.

Basics of Recursion

Recursive function is the routine which calls itself again and again.This is a simple example of a recursive function.

Example : Function to calculate the sum of numbers from 1 to given number x using recursion.

int rec(int x){
        if(x==1){          // Base Case
            return 1;
        }
        int ans=rec(x-1);  //Recursive Call
        return (ans+x);    //Small calculation
}

Recursive function has three parts:

• Base Case : A recursive function must have a base case.It's the terminating point for the function.
• Recursive Call : Here,function will call itself to solve a smaller problem.
• Small calculation : It does some calculation like addition,multiplication etc and return the value back to the function.The value returned by this calculation will further be reused for solving problem.

Types of Recursion

The types of Recursion are:

1. Direct Recursion
   1.1. Tail Recursion
   1.2. Head Recursion
2. Indirect Recursion

There are two types of recursion:

1. Direct Recursion : Recursive function calling itself is called direct recursion.

It is further categorised as :

• Tail Recursion : Recursive function which doesn't perform any operation at the returning time but does all the operations at the calling time.

Example: Function to print number from 1 to n in decreasing order recursively.

void print(int n){
    if(n == 1){
        cout << n << " ";
        return;
    }
    cout << n << " ";
    print(n - 1);
} 

• Head Recursion : Recursive function which doesn't perform any operation at the calling time but does all the operations at the returning time.

Example: Function to find out the number of digits present in a number recursively.

int count(int n){
    if(n == 0){
        return 0;
    }
    int smallAns = count(n / 10);
    return smallAns + 1;
}

2. Indirect Recursion : In this recursion,there are more than one functions and they are calling to one another in a circular manner.

Example: To print from 1 to 10 using indirect recursion.

#define N 10
int m=1;
void B();

void A(){
    if(m>N){
        return;
    }
    cout<<m<<" ";
    m++;
    B();
}

void B(){
   if(m>N){
       return;
   }
   cout<<m<<" ";
   m++;
   A();
}

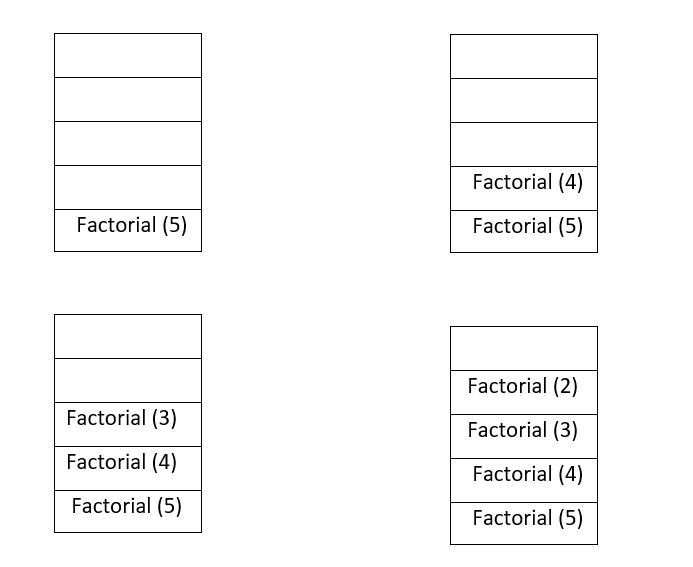
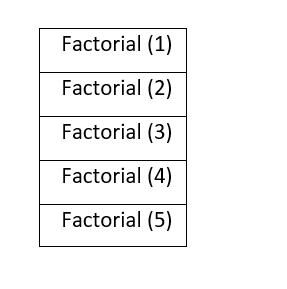
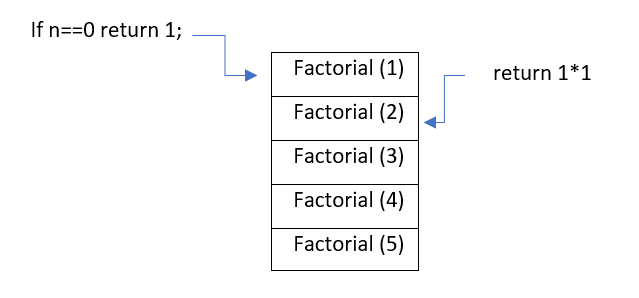
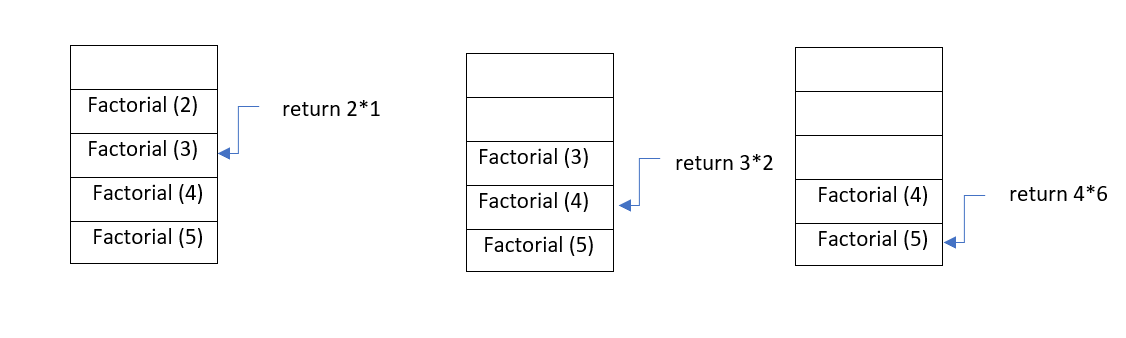
How memory is allocated to different function calls in recursion?

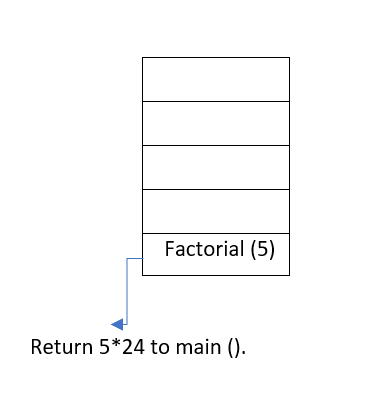
When main() calls any function then memory is allocated to it on the top of the stack. After that recursive function calls itself and the memory is allocated to a called function on the top of memory allocated to calling function.For each function call,different copy of local variables is being created.On reaching base case,the function returns its value to the function by whom it is being called and the memory is de-allocated.

Let us understand this concept with the help of an example:

Example: To find factorial of a number.

int factorial(int n){
    if(n==0){
        return 1;
    }
    return (n*factorial(n-1));
}

If n=5

Is recursion good in Programming?

Recursion is memory-intensive because the repeated function calls build up on the call stack.

So,we can say if we have not enough memory then we should avoid recursion and should use loop.But it has some advantages also like the program size would be short and easy to maintain.

Also,there are some problems which is quite easy to solve using recursion like TOH,DFS of graph etc.Talking in terms of time complexity,generally algorithm written in a recursive way or in the form of loop,they both have the same complexity.

There is an important point to note here that recursive algorithm can be made iterative.Below is an example of that.

Example : To find the factorial of a number.

1. Recursive approach

int factorial(int n){
    if(n==0){
        return 1;
    }
    return (n*factorial(n-1));
}

• Time Complexity : O(n)
• Space Complexity : O(n)

2. Iterative approach

int factorial(int n){
    int res=1;
    for(int i=2;i<=n;i++){
        res=res*i;
    }
    return res;
}

• Time Complexity : O(n)
• Space Complexity : O(1)

With this article at OpenGenus, you must have a strong idea of Recursion in Programming. Enjoy.