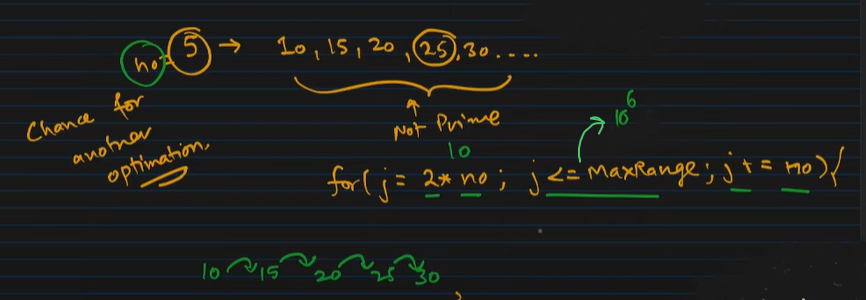Sieve of Eratosthenes is an efficient algorithm to find a list of prime numbers less than N. We have explained how the brute force approach is improved to form Sieve of Eratosthenes.

Table of contents:

1. Finding Prime Numbers
2. Brute Force approach
3. Improvement to Brute Force approach
4. Sieve of Eratosthenes
5. Questions

During competitive programming, we are often required to compute prime numbers.

Finding Prime Numbers

In math, prime numbers are whole numbers greater than 1, that have only two factors : 1 and the number itself.
Prime numbers are divisible only by the number 1 or itself.

For example, 2, 3, 5, 7 and 11 are the first few prime numbers.

Finding prime number is one of the intial program we learn when we start coding but as we reach the level of competitive programming the naive approaches are not much useful.

So SIEVE OF ERATOSTHENES is the optimal approach which would not give a TLE( time limit execute ) while competitive programming.

We will be discussing brute force approach and then Sieve of Eratosthenes

EXAMPLES:

Input : n =10
Output : 2 3 5 7

Input : n = 20
Output: 2 3 5 7 11 13 17 19

Brute Force approach

In this approach we check the number N is prime or not by that fact that if a number is divided by number other than 1 or itself . Then that number will be prime . And using nested loop we can find out the prime numbers upto N.

IMPLEMENTATION (C++)

#include<iostream>
using namespace std;
int main()
{
    int N;
    cin>>N;
    // find prime numbers less than or equal to N
    int flag = 0 ;
    for(int i = 2 ; i <= N ; i ++)
    {
        for( int j = 2 ; j < i ; j++)
        {
            if(i % j == 0 )
            {
                flag = 1;
                break;
                //number is not prime
            }
        }

        if(flag == 0)
        {
        //for printing prime numbers
        cout << i << "," ;
        }
        flag=0;
    }
    return 0;
}

OUTPUT:

N=20
2,3,5,7,11,13,17,19,

COMPLEXITY

Complexity of this approach is O(N^2).

EXPLANATION

Number N is taken as an input from user and then in first loop the traversal is taken from 2 till N and in the next loop we check that the number is checked by dividing it with all other numbers . If number has divisor other than 1 and itself . Then that number is not prime and we break from the inner loop and we print only the prime numbers using flag value.

Improvement to Brute Force approach

In this approach we come to an improvemnt where the following fact works:
to determine whether a number is prime or not instead of diving and checking with each value upto that number N.

A better approach is based on the fact that for any given number N there is atleast 1 divisor possible whcih is less than or equal to √N if that number is NOT PRIME.

IMPLEMENTATION(C++)

#include<iostream>
using namespace std;
int main()
{
    int N;
    cin>>N;
    // find prime numbers less than or equal to N
    int flag = 0 ;
    for(int i = 2 ; i <= N ; i ++)
    {
        for( int j = 2 ; j * j <= i ; j++) // j<=sqrt(i)
        {
            if(i % j == 0 )
            {
                flag = 1;
                break;
                //number is not prime
            }
        }

        if(flag == 0)
        {
        //printing all the prime numbers
        cout << i << "," ;
        }
        flag=0;
    }
}

OUTPUT:

30
2,3,5,7,11,13,17,19,23,29

COMPLEXITY

The complexity of above approach is O(N * √N).

EXPLANATION

Number N is taken as an input from user and then in first loop the traversal is taken from 2 till N and in the next loop we check that the number is checked by dividing it with numbers upto √N . If number has divisor other than 1 and itself.

Then that number is not prime and we break from the inner loop and we print only the prime numbers using flag value.

But even this complexity will be higher for large values of N.

Sieve of Eratosthenes

1) We directly generate an array containing prime numbers.
Here we keep on marking the non prime(0) options and at last we are left with UNMARKED PRIME NUMBERS(1).
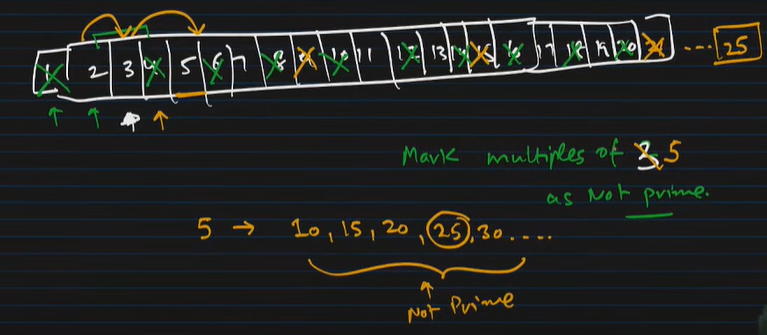
Lets discuss the process through an example :
N=20

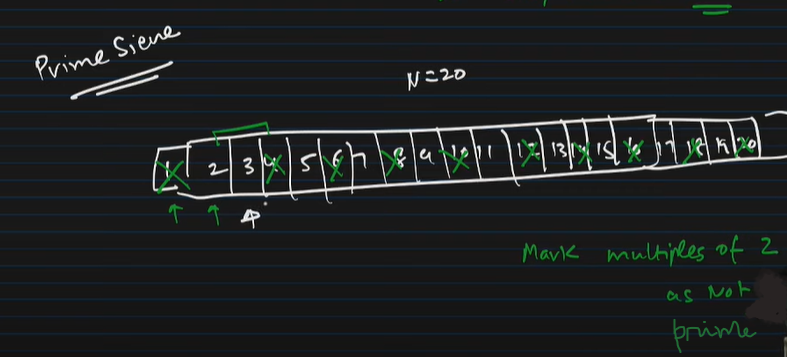
2) We start from assuming that all the numbers as prime . And we ignore 1 since it is non prime. We come to 2. Since two is not marked so it is a prime number , we work on marking all the multiples of 2 . 2= 2,4,8,10,12,14,16,18,20 as non prime .AND WE also know the fact that even numbers are not prime.
NOT MARKED INDICATES THAT THE NUMBER IS NOT A MULTIPLE OF ANY NUMBER OTHER THAN 1 . THEREFORE IT IS PRIME.

3) Here we marked all the multiples of 2. Then we come to 3. three is also not marked which means that we could not find a number which was less than 3 and could have been a divisor of 3.
3=9,15 and if there would have been 21 that also would have been marked.
We come to 4 and then 4 is already MARKED which means that it is not prime.

4)In this way we will approach this algorithm.
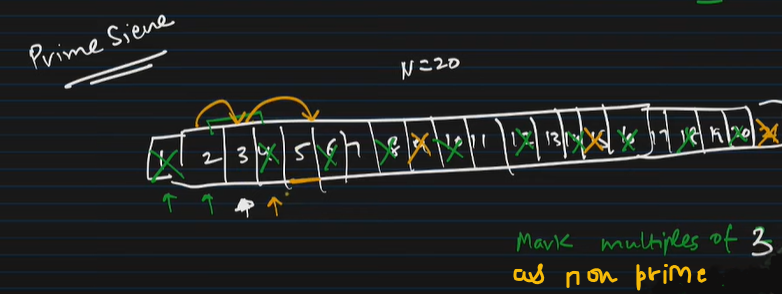
Now when we come to 5 we come to an important optimatization of this problem .
we will understand the fact that in this loop why we start traversal of inner loop
for (int i=p * p; i<=n; i += p) from p^2 not from 2 * p , because multiples of p
less than p^2 have already been marked.

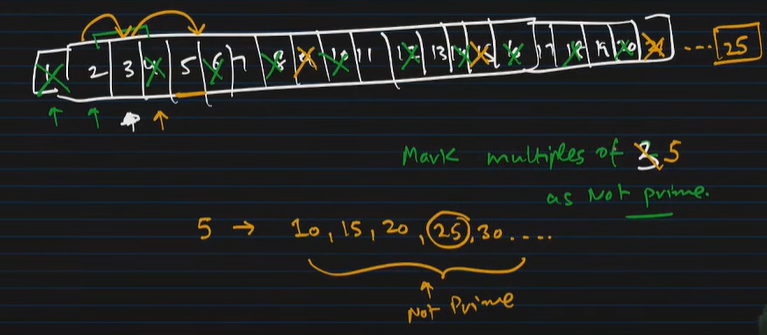
5)After finding multiples of 5 now to explain this point that why we begin loop from p * p.
if you talk about divisors of 25 which are less thqan or equal to √25/5 we have already traversed them upto 4 while referrig divisors upto √24 which is nearly 4.
then we have numbers from 1,2,3,4,5,.......,24,25.

6)so , for every p there exists a divisor less than √p which is not prime.
therefore when we come to a prime number no we will directly start marking its multiples from [no * no] rather than [2 * no] .

Last optimization is that all even numbers can be marked as non prime . we can exclude them.

ALGORITHM FOR Sieve of Eratosthenes

1)Create a list of consecutive integers from 2 to n: (2, 3, 4, …, n).
Initially, let p equal 2, the first prime number.
2)Starting from p2, count up in increments of p and mark each of these numbers
greater than or equal to p2 itself in the list. These numbers will be p(p+1),
p(p+2), p(p+3), etc..
3)Find the first number greater than p in the list that is not marked. If there
was no such number, stop. Otherwise, let p now equal this number (which is the
next prime), and repeat from step 3.

IMPLEMENTATION (C++)

#include<iostream>
using namespace std;

#define ll long long

//Sieve Approach - Generate a array containing prime numbers
void prime_sieve(int *p , int n)
{
    //first mark all odd number's prime
    for(int i = 3; i <= n ; i+=2 )
    {
        p[i] = 1;
    }

    //Sieve
    for(ll i = 3 ; i <= n ; i+=2)
    {
        //if the current number is not marked (it is prime)
        if(p[i] == 1)
        {
            //mark all the multiples of i as not prime
            for(ll j = i*i ; j <= n ; j = j+i)
            {
                p[j] = 0;
            }
        }
    }
    //special case
    p[2] = 1;
    p[1] = p[0] = 0;
}

int main()
{
    int n;
    cin>>n;

    int p[n] = {0};
    prime_sieve(p, n);

    for(int i = 0 ; i<= n ; i++)
    {
        if(p[i] == 1)
        {
                cout<< i <<" ";
        }
    }

    return 0;
}

OUTPUT:

100
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

COMPLEXITY

TIME COMPELXITY of sieb=ve of eratosthenes is O(n * log(log(n)))

Here even if we take n to be 10^18 then also it will be [n * log60] = [n * 7]
which is approximately a LINEAR COMPLEXITY.

HOW IS THE COMPLEXITY COMPUTED?

1)If it is assumed that the time taken to mark a number as composite is constant, then the number of times the loop runs is equal to:

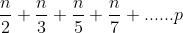
2)On taking n common from the above equation, the above equation can be rewritten as:

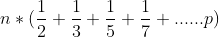
3)It can be proved as below with the help of Harmonic Progression of the sum of primes:

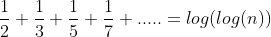
EXPANATION

We first take input from user and declare an array of size n in whcih we will directly store the prime numbers which will be marked as 1.

then we will apss on the size and array to the prime_sieve function . There first the odd numbers are marked as 1 because even numbers cannot be prime. Then we start from 3 because 1 and 2 are considered to be special cases .Now for every number which is marked as 1 (odd possiblities) we start traversing loop from i* i and then mark all the multiples by using (j=j+i) of that number i as non prime i.e 0 . Thus in the end we are left will all those numbers which are marked as 1 i.e prime .

Questions

With this article at OpenGenus, you must have the complete idea of Sieve of Eratosthenes and naive approach to find prime numbers.