Tower Of Hanoi Problem [Recursive + Iterative approach]
Tower Of Hanoi (TOH) is a mathematical puzzle which can be easily solved by recursive algorithm. It is used to demonstrate the simple rules to solve a problem and lead to exponential number of steps.
Table of contents:
- Problem statement of Tower Of Hanoi
- Algorithm for Tower Of Hanoi
- Recursive Implementation of Tower Of Hanoi
- Time & Space Complexity Analysis of Tower Of Hanoi
- Iterative approach for Tower Of Hanoi
- Iterative Implementation of Tower Of Hanoi
- Time & Space Complexity of Iterative Approach
We will get started with Tower Of Hanoi Problem now.
Problem statement of Tower Of Hanoi
Tower of Hanoi is a mathematical puzzle. It consists of three poles and a number of disks of different sizes which can slide onto any poles. The puzzle starts with the disk in ascending order of size in one pole, the smallest at the top. The objective of the puzzle is to move all the disks from one pole (source pole) to another pole (destination pole) with the help of the third pole (auxiliary pole).
There are some rules which needs to be followed at the time of solving this puzzle.
- Only one disk can be moved at a time.
- A disk can only be moved if it is the uppermost disk in the pole.
- A larger disk can't be placed on a smaller disk.
Algorithm for Tower Of Hanoi
The procedure is as follows:
- First of all, we will make a recursive call to transfer all the disks from source pole to auxiliary pole with the help of destination pole except the last disk.
- If the number of disks in the source pole is left 1 then transfer it to destination pole.This will be handled through base case.
- At last, we will make another recursive call to transfer all the disks from auxiliary pole to destination pole with the help of source pole.
Since this is a recursive approach so,it is quite difficult to understand this by just reading the algorithm so,let's take an example to have a better idea of the solution.
Example :
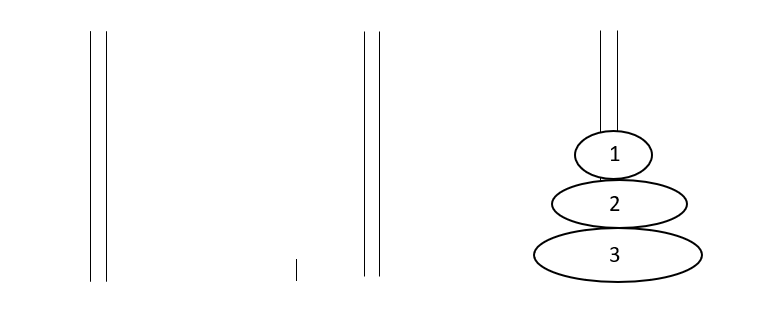
Number of disks : 3
Source pole : A
Auxiliary pole : B
Destination pole : C
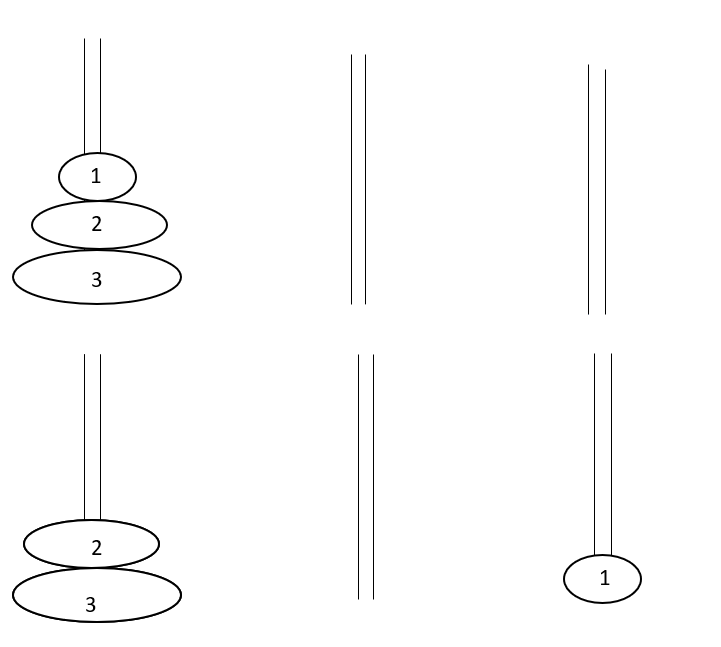
In the given fig. first pole is A,second pole is B and third pole is C
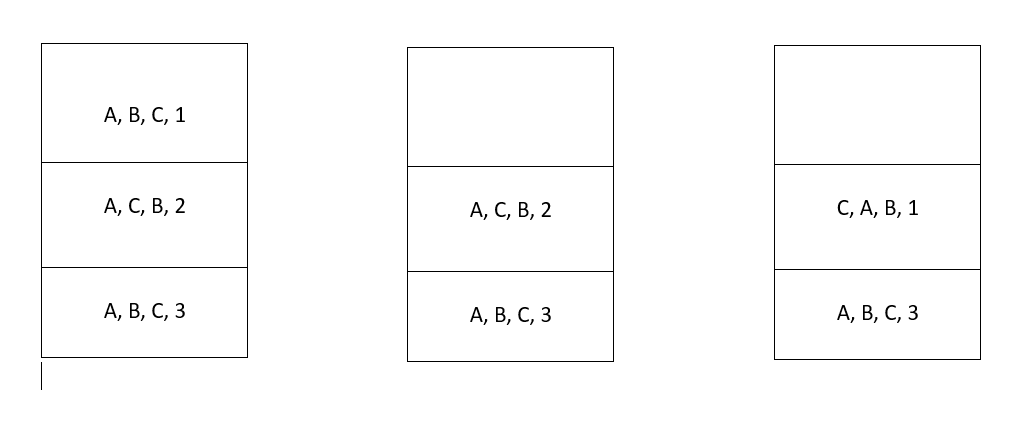
Firstly all the disks is in poleA and then the uppermost disk(smallest one) is being moved to poleC.
Now uppermost disk(second smallest one) of poleA is being moved to poleB.
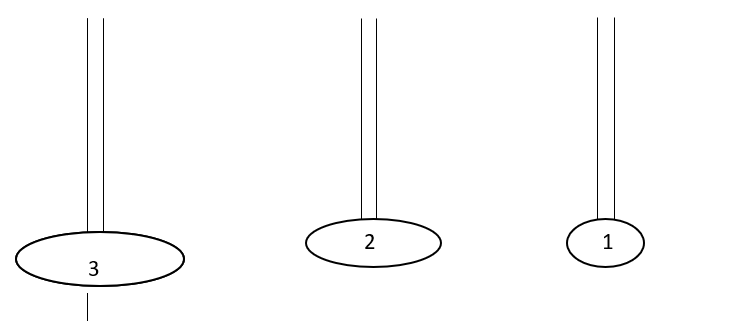
Uppermost disk(smallest one) of poleC is being moved to poleB.Then,uppermost disk(largest one) of poleA is being moved to poleC.
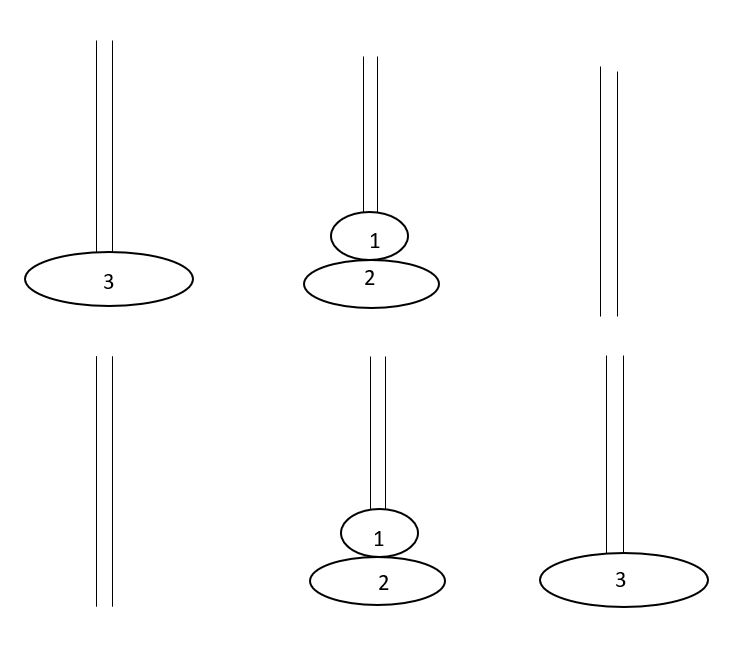
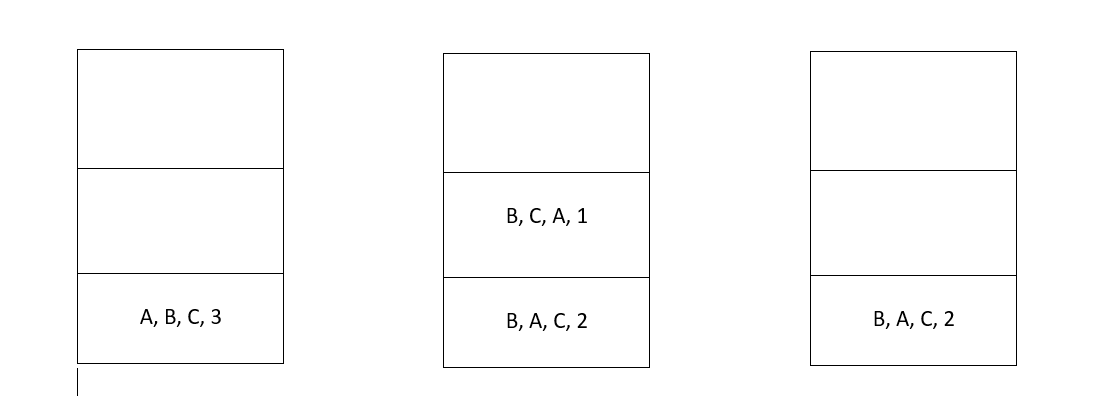
Again,uppermost disk(smallest one) of poleB is being moved to poleA.Also uppermost disk(second smallest one) of poleB is being moved to poleC.
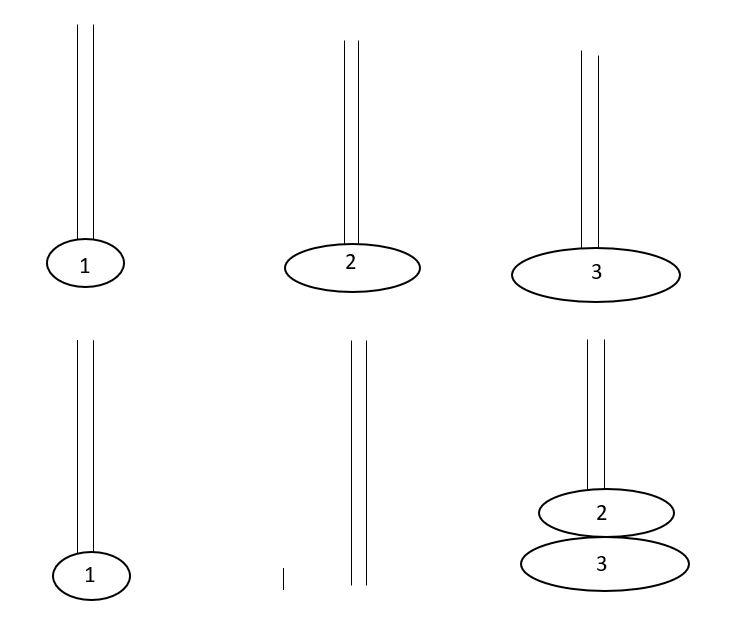
Finally,all the disks is being moved to poleC.
Recursive Implementation of Tower Of Hanoi
Recursive Implementation of Tower Of Hanoi:
#include<bits/stdc++.h>
using namespace std;
void towerOfHanoi(int n, char source, char auxiliary, char destination) {
if(n==1){
// Base Case : If number of disk left in source pole is 1 then move the disk to destination pole.
cout << "Move disk 1 from rod " << source <<
" to rod " << destination <<endl;
return;
}
towerOfHanoi(n-1,source,destination,auxiliary);
// Move n-1 disks from source pole to auxiliary pole with the help of destination pole.
cout << "Move disk " << n << " from rod " << source <<
" to rod " << destination << endl;
towerOfHanoi(n-1,auxiliary,source,destination);
// Move n-1 disks from auxiliary pole to destination pole with the help of source pole.
}
int main(){
int n; // Number of disks
cin>>n;
towerOfHanoi(n,'A','B','C');
return 0;
}
Output :
3
Move disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C
Time & Space Complexity Analysis of Tower Of Hanoi
Recursive equation:
T(n)= 2 * T(n-1) + 1 -----> (1)
where n is the number of disks.
Since we are making two recursive calls on (n-1) disks
so,2 * T(n-1) is there in the equation and 1 is added for constant work like for cout statement.
Termination condition : T(0) = 1 , if number of disks become 0 then no need to do any work just return.
On solving equation (1) :
- Time Complexity : O(2^n)
Soace Complexity: O(2^N)
Due to recursive calls that are stacked up internally.
Iterative approach for Tower Of Hanoi
In iterative approach,we will try to convert our recursive idea into iterative one.The data structure involved is stack.The procedure is as follows:
-
In recursive approach till n becomes 1 we have called the recursive function by swapping destination pole and auxiliary pole, that is what we are going to do here
till n becomes 1 we will put a variable into stack which makes a track of source, auxiliary and destination pole. -
If n becomes 1 then we will pop the variable from the stack and print it.
-
Same as our second recursive call where we are continuously again making a call by swapping source and auxiliary pole till n becomes 1.
Let's take an example
Example :
Number of disks : 3
Source pole : A
Auxiliary pole : B
Destination pole : C
In the stack,we were storing source,auxiliary,destination pole and the number of disks left after that disk.Whenever it comes out to be 1 we are removing it from stack and then printing it.
Iterative Implementation of Tower Of Hanoi
Recursive Implementation of Tower Of Hanoi:
#include<bits/stdc++.h>
using namespace std;
class toh{ //To make a variable which can keep a track of source, auxiliary and destination pole.
public:
char from;
char to;
char aux;
int n;
};
void towerOfHanoi(int n, char source, char auxiliary, char destination){
stack<toh> st; //Declaring a stack.
while(n>=1 or !st.empty()){
while(n>=1){ //Save the current state and move to the towerOfHanoi(n-1,source,destination,auxiliary).
toh cur;
cur.from=source;
cur.aux=auxiliary;
cur.to=destination;
cur.n=n;
st.push(cur);
swap(destination,auxiliary);
n--;
}
toh cur = st.top();
st.pop();
cout << "Move disk " << cur.n << " from rod " << cur.from <<
" to rod " << cur.to << endl;
if(cur.n>=1){
source=cur.aux; // Simulates the towerOfHanoi(n-1,auxiliary,source,destination) of Recursive Step.
auxiliary=cur.from;
destination=cur.to;
n=cur.n-1;
}
}
}
int main(){
int n; // Number of disks.
cin>>n;
towerOfHanoi(n,'A','B','C');
return 0;
}
Output :
3
Move disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C
Time & Space Complexity of Iterative Approach
-
Time Complexity : O(2^N)
This is same as recursive approach because the basic idea and logic is same. -
Space Complexity : O(2^N)
This is due to the stack size.
With this article at OpenGenus, you must have the complete idea of Tower Of Hanoi along with its implementation and Time and Space complexity Analysis.