Weighted Job scheduling problem [4 solutions]
In this article, we have solved the Weighted Job scheduling problem with 4 detailed solutions including Greedy approach, Dynamic Programming, Brute force and DP with Binary Search.
Table of content:
- Problem statement: Weighted Job scheduling
- Naive Recursive approach
- Dynamic Programming Approach
- Weighted Problem with Dynamic Programming
- DYNAMIC PROGRAMMING (USING BINARY SEARCH)
- GREEDY METHOD (JOB SEQUENCING PROBLEM) (RESTRICTED APPROACH)
- QUESTIONS
Problem statement: Weighted Job scheduling
In this problem, there are N jobs and we are given with some characteristics of job based on which our task is to find a subset of jobs, where the profit is maximum and no jobs are overlapping each other.
Characteristics of the job are :
a) Start Time of the job
b) Finish Time of the job
c) Every job has a profit associated to it.
Here non overlapping means that if there are two jobs in which the start time of second job is between the start and finsh time of first job , then those two jobs are siad to be overlapping to each other and thus we cannot add up profit of those two jobs.
Underlying are some examples which will explain how we are supposed to monitor profit of each job .
Example:
Input: Number of Jobs n = 4
Job Details {Start Time, Finish Time, Profit}
Job 1: {1, 2, 50}
Job 2: {3, 5, 20}
Job 3: {6, 19, 100}
Job 4: {2, 100, 200}
Output: The maximum profit is 250.
We can get the maximum profit by scheduling jobs 1 and 4.
Note that there is longer schedules possible Jobs 1, 2 and 3
but the profit with this schedule is 20+50+100 which is less than 250.
In this example job details can be treated as structure (struct) .But the question can also be framed as with different arrays for all three components of a job which is described below.
Structure is a collection of variables of different data types under a single name. It is similar to a class in that, both holds a collecion of data of different data types.
For example: You want to store some information about a person: his/her name, citizenship number and salary. You can easily create different variables name, citNo, salary to store these information separately.
Other examples:
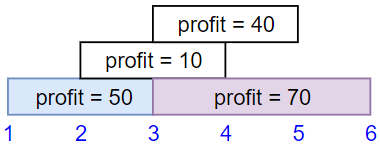
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
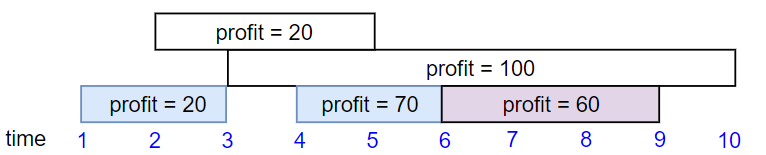
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

There are many approaches for this problem:
- The activity problem is the basic format of this problem (restricted version) which can be solved using GREEDY METHOD.
- Then first of all, we have a Naive Recursive Approach.
- Dynamic Programming Approach.
- Dynamic Programming approach using Binary Search.
Naive Recursive approach
The idea is to sort the jobs in increasing order of their finish time and then use recursion to solve this problem.Also finding the recursive approach is first step to dynamic Programming. Here we find the pattern that for every job we have to find a non conflicting job and add up their profits and that is what is done by excluding current job and including current job after sorting the array on the basis of their finish time.
ALGORITHM
- First sort jobs according to finish time.
- Now apply following recursive process.
// Here arr[] is array of n jobs
findMaximumProfit(arr[], n)
{
a) if (n == 1)
return arr[0];
b) Return the maximum of following two profits.
(i) Maximum profit by excluding current job, i.e.,
findMaximumProfit(arr, n-1)
(ii) Maximum profit by including the current job
}
How to find the profit including current job?
For finding non conflicting job we start our traversal from end and we look for the first job from end(latest job) which does not conflict with the curresnt jon(arr[n-1]) i.e job4.
The idea is to find the latest job before the current job (in sorted array) that doesn't conflict with current job 'arr[n-1]'. Once we find such a job, we recur for all jobs till that job and add profit of current job to result.
Job Details {Start Time, Finish Time, Profit}
Job 1: {1, 2, 50}
Job 2: {3, 5, 20}
Job 3: {6, 19, 100}
Job 4: {2, 100, 200}
In the above example, "job 1" is the latest non-conflicting
for "job 4" and "job 2" is the latest non-conflicting for "job 3".
IMPLEMENTATION(C++) USING STRUCTURE
// C++ program for weighted job scheduling using Naive Recursive Method
#include <iostream>
#include <algorithm>
using namespace std;
// A job has start time, finish time and profit.
struct Job
{
int start, finish, profit;
};
// A utility function that is used for sorting events
// according to finish time
bool jobComparataor(Job s1, Job s2)
{
return (s1.finish < s2.finish);
}
// Find the latest job (in sorted array) that doesn't
// conflict with the job[i]. If there is no compatible job,
// then it returns -1.
int latestNonConflict(Job arr[], int i)
{
for (int j=i-1; j>=0; j--)
{
if (arr[j].finish <= arr[i-1].start)
return j;
}
return -1;
}
// A recursive function that returns the maximum possible
// profit from given array of jobs. The array of jobs must
// be sorted according to finish time.
int findMaxProfitRec(Job arr[], int n)
{
// Base case
if (n == 1) return arr[n-1].profit;
// Find profit when current job is included
int inclProf = arr[n-1].profit;
int i = latestNonConflict(arr, n);
if (i != -1)
inclProf += findMaxProfitRec(arr, i+1);
// Find profit when current job is excluded
int exclProf = findMaxProfitRec(arr, n-1);
return max(inclProf, exclProf);
}
// The main function that returns the maximum possible
// profit from given array of jobs
int findMaxProfit(Job arr[], int n)
{
// Sort jobs according to finish time
sort(arr, arr+n, jobComparataor);
return findMaxProfitRec(arr, n);
}
// Driver program
int main()
{
Job arr[] = {{3, 10, 20}, {1, 2, 50}, {6, 19, 100}, {2, 100, 200}};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "The optimal profit is " << findMaxProfit(arr, n);
return 0;
}
OUTPUT:
The optimal profit is 250
COMPLEXITY
The above solution may contain many overlapping subproblems. For example if
lastNonConflicting() always returns previous job, then findMaxProfitRec(arr, n-1) is called twice and the time complexity becomes O(n*2ⁿ).
EXPLANATION
Structure is a collection of variables of different data types under a single name. It is similar to a class in that, both holds a collecion of data of different data types.
We compute the size of the array of type structure in n, and furthur in findMaxProfit(Job arr[], int n). we first sort the array using comparator function which sorts according to the finish time of the each job in ascending order .
Then the sorted array is passed into findMaxProfitRec(Job arr[], int n) funtion where start checking start time of one job(with the last job) with the finsih time of every other job with the help of latestNonConflict(Job arr[], int i) function and return the index with no conflict .We reucursively solve call findMaxProfitRec(Job arr[], int n) and findMaxProfitRec(Job arr[], int n-1) till we get non overlapping jobs . And finally we calculate the maximum of two whcih is our final profit.
Dynamic Programming Approach
Before coming to the solution of this problem , lets discuss Dynamic problem with an easier example.
WHAT IS DYNAMIC PROGRAMMING?
Dynamic programming is way of making your algorithm more efficient by storing some of the intermediate results. It works really well when our problem has repetitive computations and with the help of DP you dont have to repeat computations over and over again.
First major property that we associate to Dynamic programming is that the problem should be recusrsive in nature .In most of the problem we optimise the recursive solution.
There is a certain set of problem which can be solved using Dynamic programming.
For those problems there exists two characteristics for which lets look at an example.
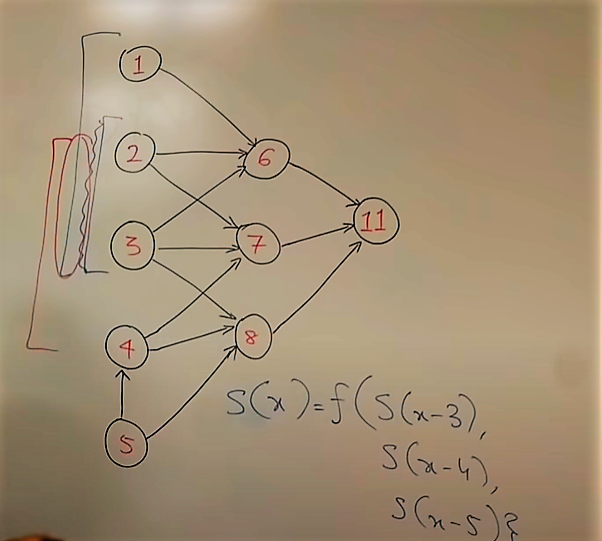
In this example to reach any state (node) we cam move throgh other states and it follows same pattern until we reach our desired state .This can be expressed by a mathematical formula that any state (node) is a function of previous three nodes .
S(x) = func[ S(x-3) , S(x-4) , S(x-5)]
What we have here is recursion because we have a problem of one type and we are breaking it into problems of same type and we are not breaking it into smaller problem that would be divide and conquer. Recursion can be diverging as well as converging.
1)Overlapping Subproblems: when we use DP there should be some benefit . Here For computing 11 , we have to compute 6,7,8 and for computing 6 we compute 1,2,3 and now when we compute 7 , we have to compute 2,3,4 but 2,3 is the overlapping subproblem which has already been computed while computing 6 . Already computed part is overlapping part.
2)Optimal Substructure: if you are at state x then the prompts that you need to solve to get here(at x) are smaller than state itself. Meaning that you are going for smaller and smaller sub problems and are individually solving those and when you are done solving those sub problems you have whole current problem solved . This is known as optimal substructure.
In simple term we mainly have 2 approaches to solve :
1)Top down approach(Memoized): In this example if we start solving from top i.e 11 we will then move to 6,7,8 and then individually we go for 6 and then for 1,2,3 and then for 7 we do not solve the overlapping part and so on we move to every node.
- Bottom Up approach: In this example we start from bottom i.e 1 and move to 2 ,3,4 and 5 after computing them the next layer completely depends on this layer and we dont need to worry about whether the nodes (subproblems) of second layer are computed or not because they are already computed . and in this way we follow bottom up approach.
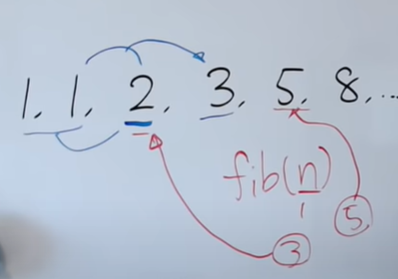
FIBONACCI SERIES WITH DP
Given below is the fibbonaci series and we have to compute the n'th term of the the series through a function fib(n).
We make a recursive solution of this problem .
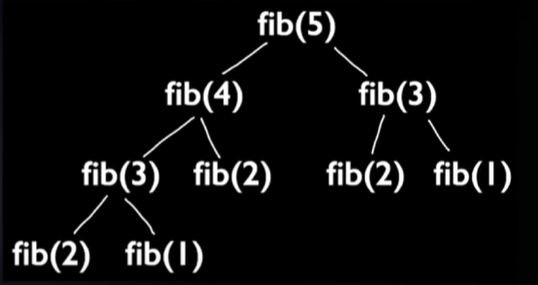
And then this is an inefficient method because for smaller number the computation time is small but for larger number it grows exponentially.Lets see how
for finding value of fib(5) we first need to compute fib(4) and fib(3) and for them we need fib(2) and fib(1) and fib(1) and fib(2) are overlapping subproblems because we need to compute them again and again . And becuase of this approach the complexity of this algorithm is O(2ⁿ).
Memoized(Top-down)
We take an array memowhose length is n+1 and initialise it with null before we call fibonacci function .We are goign to store return value of fib(n) at an index n . If we have already stored the required value in memo we directly return it . The complexity of this approach is O(n).
Bottom-up
Storing base values and using them later is the basic idea behind this approach.We take a bottom-up array and store the values by computing it for every number upto n and then returning the final value. The complexity of this approach is O(n).
Weighted Problem with Dynamic Programming
Now we come to the algorithm of our weighted problem:
After finding recursive approach we see that there are subproblems for which we are computing profit again and again.
So here , we take a table .It declares a pointer to a dynamic array of type int and size n which is pointing to the profit of first job after being sorted.
HOW IT IS DIFFERENT FROM RECURSION?
In this approach we thought that our table[i] entries will be stored in such a way that when we find the latest non conflicting job then instead of adding profits of every non conflicting job ,we addprofit of the current job and non conflicting job and then compare it with the previous table entry. If our calculated profit i.e
addprofit is greater, than we store that to table otherwise we keep the previous value of the table[i-1]. Since that previous value will be greater . So here we save a lot of computations by keeping the greatest profit upto that job.
ALGORITHM
findMaxProfit(jobList, n)
Input: The job list and number of jobs.
Output: Maximum profit from the jobs.
Begin
sort job list according to their ending time
define table to store results
table[0] := jobList[0].profit
for i := 1 to n-1, do
addProfit := jobList[i].profit
nonConflict := find jobs which is not conflicting with others
if any non-conflicting job found, then
addProfit := addProfit + table[nonConflict]
if addProfit > table[i - 1], then
table[i] := addProfit
else
table[i] := table[i-1]
done
result := table[n-1]
return result
End
IMPLEMENTATION (C++) USING STRUCTURE
#include <iostream>
#include <algorithm>
using namespace std;
struct Job {
int start, end, profit;
};
bool comp(Job job1, Job job2) {
return (job1.end < job2.end);
}
int nonConflictJob(Job jobList[], int i) { //non conflicting job of jobList[i]
for (int j=i-1; j>=0; j--) {
if (jobList[j].end <= jobList[i-1].start)
return j;
}
return -1;
}
int findMaxProfit(Job jobList[], int n) {
sort(jobList, jobList+n, comp); //sort jobs based on the ending time
int *table = new int[n]; //create job table
table[0] = jobList[0].profit;
for (int i=1; i<n; i++) {
// Find profit including the current job
int addProfit = jobList[i].profit;
int l = nonConflictJob(jobList, i);
if (l != -1)
addProfit += table[l];
table[i] = (addProfit>table[i-1])?addProfit:table[i-1]; //find maximum
}
int result = table[n-1];
delete[] table; //clear table from memory
return result;
}
int main() {
Job jobList[] = {
{3, 5, 25},
{1, 2, 50},
{6, 15, 75},
{2, 100, 100}
};
int n = 4;
cout << "The maximum profit: " << findMaxProfit(jobList, n);
return 0;
}
OUTPUT:
The optimal profit is 150
COMPLEXITY
Time Complexity of the above Dynamic Programming Solution is O(n²).
EXPLANATION
Here we first sort the given array according to the finish time of the job . A new table is created which will store the corresponding profit as we go on the find the maximum profit. This will help us to not repeat the process of comparing everytime and calculating the results we already went through once while comparing profits and end time of each job.This is the Dyanamic approach.
For each job through a loop we call nonConflictJob(jobList, i) which is used to find the index(l) of job whose time do not overlap with the current job index. Then we add profit from table[i-1] or addProfit += table[l]; depending upon ehich ever is greater among two is stroed into the table. Int his way we keep a contigous Maximum array stored into table and we need not to compute profit again and again for all the previous jobs of a particular job.
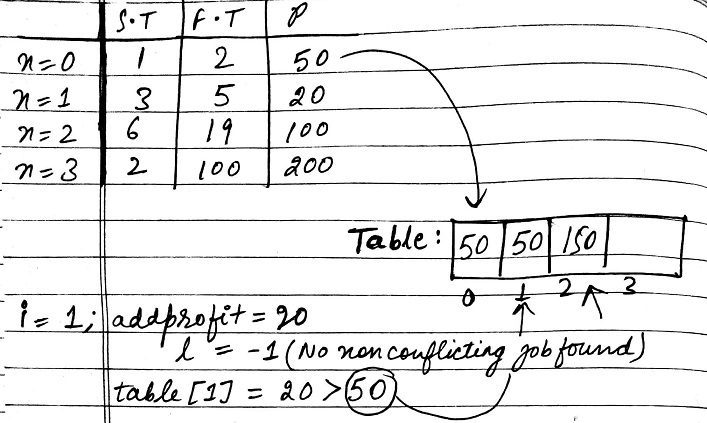
Here in this example then we see that table is being build up in a form that we are keeping cummulative profit thus reducing our computations.

In programming, Dynamic Programming is a powerful technique that allows one to solve different types of problems in time O(n^2) or O(n^3) for which a naive approach would take exponential time.
DYNAMIC PROGRAMMING (USING BINARY SEARCH)
The implementations discussed in above post uses linear search to find the previous non-conflicting job. In this post, Binary Search based solution is discussed. The time complexity of Binary Search based solution is O(n Log n).
ALGORITHM
1)Sort the jobs by non-decreasing finish times.
2)For each i from 1 to n, determine the maximum value of the schedule from the
subsequence of jobs[0..i]. Do this by comparing the inclusion of job[i] to the
schedule to the exclusion of job[i] to the schedule, and then taking the max.
3)To find the profit with inclusion of job[i]. we need to find the latest job
that doesn’t conflict with job[i]. The idea is to use Binary Search to find the
latest non-conflicting job.
IMPLEMENTATION (C++) USING STRUCTURE
// C++ program for weighted job scheduling using Dynamic
// Programming and Binary Search
#include <iostream>
#include <algorithm>
using namespace std;
// A job has start time, finish time and profit.
struct Job
{
int start, finish, profit;
};
// A utility function that is used for sorting events
// according to finish time
bool myfunction(Job s1, Job s2)
{
return (s1.finish < s2.finish);
}
// A Binary Search based function to find the latest job
// (before current job) that doesn't conflict with current
// job. "index" is index of the current job. This function
// returns -1 if all jobs before index conflict with it.
// The array jobs[] is sorted in increasing order of finish
// time.
int binarySearch(Job jobs[], int index)
{
// Initialize 'lo' and 'hi' for Binary Search
int lo = 0, hi = index - 1;
// Perform binary Search iteratively
while (lo <= hi)
{
int mid = (lo + hi) / 2;
if (jobs[mid].finish <= jobs[index].start)
{
if (jobs[mid + 1].finish <= jobs[index].start)
lo = mid + 1;
else
return mid;
}
else
hi = mid - 1;
}
return -1;
}
// The main function that returns the maximum possible
// profit from given array of jobs
int findMaxProfit(Job arr[], int n)
{
// Sort jobs according to finish time
sort(arr, arr+n, myfunction);
// Create an array to store solutions of subproblems. table[i]
// stores the profit for jobs till arr[i] (including arr[i])
int *table = new int[n];
table[0] = arr[0].profit;
// Fill entries in table[] using recursive property
for (int i=1; i<n; i++)
{
// Find profit including the current job
int inclProf = arr[i].profit;
int l = binarySearch(arr, i);
if (l != -1)
inclProf += table[l];
// Store maximum of including and excluding
table[i] = max(inclProf, table[i-1]);
}
// Store result and free dynamic memory allocated for table[]
int result = table[n-1];
delete[] table;
return result;
}
// Driver program
int main()
{
Job arr[] = {{3, 10, 20}, {1, 2, 50}, {6, 19, 100}, {2, 100, 200}};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Optimal profit is " << findMaxProfit(arr, n);
return 0;
}
OUTPUT:
The optimal profit is 250.
COMPLEXITY
Time Complexity of the above Dynamic Programming Solution is O(nLogn).
EXPLANATION
Here we first sort the given array according to the finish time of the job .A new table is created which will store the corresponding profit as we go on the find the maximum profit. This will help us to not repeat the process of comparing everytime and calculating the results we already went through once while comparing profits and end time of each job.This is the Dyanamic approach.In this program intead of traversing the loop n times for finding the non conflicting job we use binary search for getting the index of non conflicting job .
This is the only difference which makes the complexity of program to go to O(nlogn). Rest of the program remains same.
GREEDY METHOD (JOB SEQUENCING PROBLEM) (RESTRICTED APPROACH)
Given an array of jobs where every job has a deadline and associated profit if the job is finished before the deadline. It is also given that every job takes single unit of time, so the minimum possible deadline for any job is 1. How to maximize total profit if only one job can be scheduled at a time.
Examples:
Input: Four Jobs with following
deadlines and profits
JobID Deadline Profit
a 4 20
b 1 10
c 1 40
d 1 30
Output: Following is maximum
profit sequence of jobs
c, a
Input: Five Jobs with following
deadlines and profits
JobID Deadline Profit
a 2 100
b 1 19
c 2 27
d 1 25
e 3 15
Output: Following is maximum
profit sequence of jobs
c, a, e
ALGORITHM
This is a standard Greedy Algorithm problem. Following is algorithm.
-
Sort all jobs in decreasing order of profit.
-
Iterate on jobs in decreasing order of profit.For each job , do the following:
a)Find a time slot i, such that slot is empty and i < deadline and i is
greatest.Put the job in
this slot and mark this slot filled.
b)If no such i exists, then ignore the job.
IMPLEMENTATION
#include<iostream>
#include<algorithm>
using namespace std;
// A structure to represent a job
struct Job
{
char id; // Job Id
int dead; // Deadline of job
int profit; // Profit if job is over before or on deadline
};
// This function is used for sorting all jobs according to profit
bool comparison(Job a, Job b)
{
return (a.profit > b.profit);
}
// Returns minimum number of platforms reqquired
void printJobScheduling(Job arr[], int n)
{
// Sort all jobs according to decreasing order of prfit
sort(arr, arr+n, comparison);
int result[n]; // To store result (Sequence of jobs)
bool slot[n]; // To keep track of free time slots
// Initialize all slots to be free
for (int i=0; i<n; i++)
slot[i] = false;
// Iterate through all given jobs
for (int i=0; i<n; i++)
{
// Find a free slot for this job (Note that we start
// from the last possible slot)
for (int j=min(n, arr[i].dead)-1; j>=0; j--)
{
// Free slot found
if (slot[j]==false)
{
result[j] = i; // Add this job to result
slot[j] = true; // Make this slot occupied
break;
}
}
}
// Print the result
for (int i=0; i<n; i++)
if (slot[i])
cout << arr[result[i]].id << " ";
}
// Driver program to test methods
int main()
{
Job arr[] = { {'a', 2, 100}, {'b', 1, 19}, {'c', 2, 27},
{'d', 1, 25}, {'e', 3, 15}};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Following is maximum profit sequence of jobsn";
printJobScheduling(arr, n);
return 0;
}
OUTPUT:
Following is maximum profit sequence of jobs
c a e
COMPLEXITY
Time Complexity of the above Solution is O(n²).
QUESTIONS
What is the time complexity of binary search algorithm?
what work by recursively constructing a set of objects from the smallest possible constituent parts.
Greedy Algorithm
Dynamic Programming
Recursion
None of these
With this article at OpenGenus, you must have a strong idea of Weighted Job scheduling problem.