Huffman Decoding [explained with example]
Huffman Decoding is a Greedy algorithm to convert an encoded string to the original string. The string had been encoded by Huffman Encoding algorithm. We have explained Huffman Decoding algorithm with Implementation and example.
Table of content:
- Basics of Decoding a message
- Huffman Decoding Algorithm
- Implementation of Huffman Decoding using C++ STL
- Another approach
- Time & Space Complexity
- Question
Prerequisite: Huffman Encoding with example and implementation
Huffman Encoding is the prerequisite as it is used to generate the encoded string. Understanding this will help you understand the Huffman Decoding algorithm easily.
We will dive into Huffman Decoding Algorithm now.
Basics of Decoding a message
What is decoding?
Suppose we have a text file and we want to store it so that it takes minimum memory.Then in these cases what we does is to convert the text file into binar y file where each character is being assigned a codeword.Sometimes,we perform this task also so that a comman people doesn't understand what is written there in the file.This is encoding and reverse of encoding is what we call as decoding.While decoding time we try to convert the codewords into some other format so that human being can understand what is written in the file.
Before going into the Huffman Decoding.Let's recall what is Huffman Encoding? Huffman Encoding is a variable-length encoding where each character is being assigned a variable-length codes based on their frequency in the given text.
But this leads to umambiguous decoding.We might have more than one interpretation for an encoded message.Because of which we also try to ensure whatever codewords is being assigned to the character should be the prefix code i.e. no codeword should be the prefix of other.Huffman encoding and decoding is important for the compression of a file.Problem statement while encoding and decoding is:
Encoding:
Given a text assign codewords to each character present in the text based on their frequency in the text.In this case first of all,we build Huffman tree where the leaf is the one storing character and by traversing on the tree we assign codewords to each character.Codewords mean in the form 0 or 1.
Decoding:
Given the Huffman Tree or you can obtain it using encoding.An encoded string in the form of 0 and 1 would be given and we have to find the decoded string using Huffman tree.
Huffman Decoding Algorithm
For decoding, the encoded string is generated using the Huffman tree using encoding algorithm and as the next step, we need to iterate over the binary encoded data.
Steps of Huffman Decoding are:
- Start from the root node.
- If the current bit in the given data is 0,then move to the left node of the tree.
- If the current bit in the given data is 1,then move to the right node of the tree.
- During the traversal if leaf node is encountered then print character of that leaf node.
- Again continue the iteration of the encoded data starting from step 1.
The pseudocode of the decode function is as follows:
string decode(struct MinHeapNode* root, string str)
{
string out = "";
//MinHeapNode is a structure Which basically defines the node of the tree
storing input character,their frequency and
also left and right child of node.
struct MinHeapNode* curr = root;
for (int i=0;i<str.size();i++){
if (str[i] == '0'){
//if current bit is 0 move to the left node.
curr = curr->left;
}else{
//if current bit is 1 move to the right node.
curr = curr->right;
}
//leaf node is encountered
if (curr->left==NULL and curr->right==NULL){
out += curr->data;
curr = root;
}
}
return out+'\0';
}
Implementation of Huffman Decoding using C++ STL
Here we are going to perform both: full Huffman encoding and decoding.
In this case we have an input string,we will encode it and save it in a variable.Then encoded string will be decoded and then finally print the original string.
Data Structure Involved:
- Priority Queue : Priority Queue is a data structure where every item has a priority associated with it and an element with high priority is dequeued before an element with low priority.It can be implemented using binary heap.
Binary heap can be either minheap or maxheap.In minheap,the tree is complete and the item at root must be minimum among all the items present in heap.This is recursively true for all the other nodes in the binary tree.Similarly in max heap the item at root must be maximum among all the items present in heap.Here we are going to use minheap implementation of Priority Queue.
By default,C++ creates a maxheap for priority queue.
Syntax : priority_queue<datatype> name_of_priority_queue
Minheap for priority queue
Syntax : priority_queue<datatype,vector<datatype>,compare>name_of_priority_queue
compare is a function which helps user to decide the priority according to which element should be arranged in the queue. In the Huffman encoding implementation, according to frequency element would be arranged in the queue.Element having least frequency would be at the root of the heap.
Methods supported by priority_queue:
- priority_queue::push() -> This function adds the element at the end of the queue and then elements arrange themselves according to the priority.
- priority_queue::top() -> Returns a reference to the top most element of the queue.
- priority_queue::pop() -> Deletes the first element of the queue and then elements arrange themselves according to the priority.
- Map : Map is like a container which stores elements as a combination of key value and mapped value.It is implemented using hash table.Both key value and mapped value can be of any data type.Key value is used to uniquely identify the element i.e. no two mapped values can have same key values.On an average the cost of search,average and delete from a hash table is O(1).
Methods supported by map:
- map::begin() –> Returns an iterator to the first element in the map.
- map::end() –> Returns an iterator to the last element in the map.
- map::size() –> Returns the number of elements in the map.
- pair insert(keyvalue, mapvalue) –> Adds a new element to the map.
Syntax for defining a map
Syntax : map<datatype,datatype> map_name
Let's now learn about a very important concept.
- Iterator : It is like a pointer that points to an element inside the container. It can be used to move through the contents of the container.It reduces the complexity and execution time of the program.
Methods supported by iterator:
- begin() -> To return the beginning position of the container.
- end() -> To return the after end position of the container.
Suppose we want to define an iterator which iterates over the element of the map:
Syntax : map<datatype,datatype> ::iterator it=map_name.begin()
//Huffman Code
#include <bits/stdc++.h>
using namespace std;
// To store the frequency of character of the input data
map<char, int> frequency;
// To store character and huffman code assigned to each character.
map<char, string> code;
// A Huffman tree node
struct MinHeapNode
{
char ele;
int freq;
MinHeapNode *left, *right;
MinHeapNode(char ele, int freq)
{
left = right = NULL;
this->ele = ele;
this->freq = freq;
}
};
// Function which tells how elements should be arranged in the priority queue
i.e. on the basis of frequency.
struct compare
{
bool operator()(MinHeapNode* l, MinHeapNode* r)
{
return (l->freq > r->freq);
}
};
//Function to print character with their codes.
void printCode(struct MinHeapNode* root, string str)
{
if (!root)
return;
if (root->data != '$')
cout << root->data << ": " << str << "\n";
printCode(root->left, str + "0");
printCode(root->right, str + "1");
}
//To store characters and their code in a hash table.
void storeCode(struct MinHeapNode* root, string str)
{
if (root==NULL)
return;
if (root->data != '$')
code[root->data]=str;
storeCode(root->left, str + "0");
storeCode(root->right, str + "1");
}
priority_queue<MinHeapNode*, vector<MinHeapNode*>, compare> pq;
// To build Huffman Tree
void Huffman(int size)
{
struct MinHeapNode *left, *right, *temp;
map<char,int> :: iterator it=frequency.begin();
while(it!=frequency.end()){
pq.push(new MinheapNode(it->first,it->second));
it++;
}
while (pq.size() != 1)
{
left = pq.top();
pq.pop();
right = pq.top();
pq.pop();
temp = new MinHeapNode('$', left->freq + right->freq);
temp->left = left;
temp->right = right;
pq.push(temp);
}
storeCode(pq.top(), "");
}
//To decode the encoded string
string decode(struct MinHeapNode* root, string str)
{
string out = "";
struct MinHeapNode* curr = root;
for (int i=0;i<str.size();i++){
if (str[i] == '0'){
//if current bit is 0 move to the left node.
curr = curr->left;
}else{
//if current bit is 1 move to the right node.
curr = curr->right;
}
//leaf node is encountered
if (curr->left==NULL and curr->right==NULL){
out += curr->data;
curr = root;
}
}
return out+'\0';
}
int main()
{
string str = "opengenus";
string s1,s2;
for (int i=0; i<str.size(); i++){
frequency[str[i]]++;
}
Huffman(str.length());
cout << "Character With there Huffman codes:"<<endl;
map<char,string> ::iterator it=code.begin();
while(it!=code.end()){
cout<<it->first<<" "<<it->second<<endl;
it++;
}
for(int i=0;i<str.size();i++){
s1=s1+code[str[i]];
}
cout << "Encoded Huffman data:" << s1 << endl;
s2 = decode(pq.top(),s1);
cout << "Decoded Huffman Data:" << s2 << endl;
return 0;
}
Output:
Character With there Huffman codes:
e 10
g 010
n 111
o 001
p 110
s 011
u 000
Encoded Huffman data:
0011101011101010111000011
Decoded Huffman Data:
opengenus
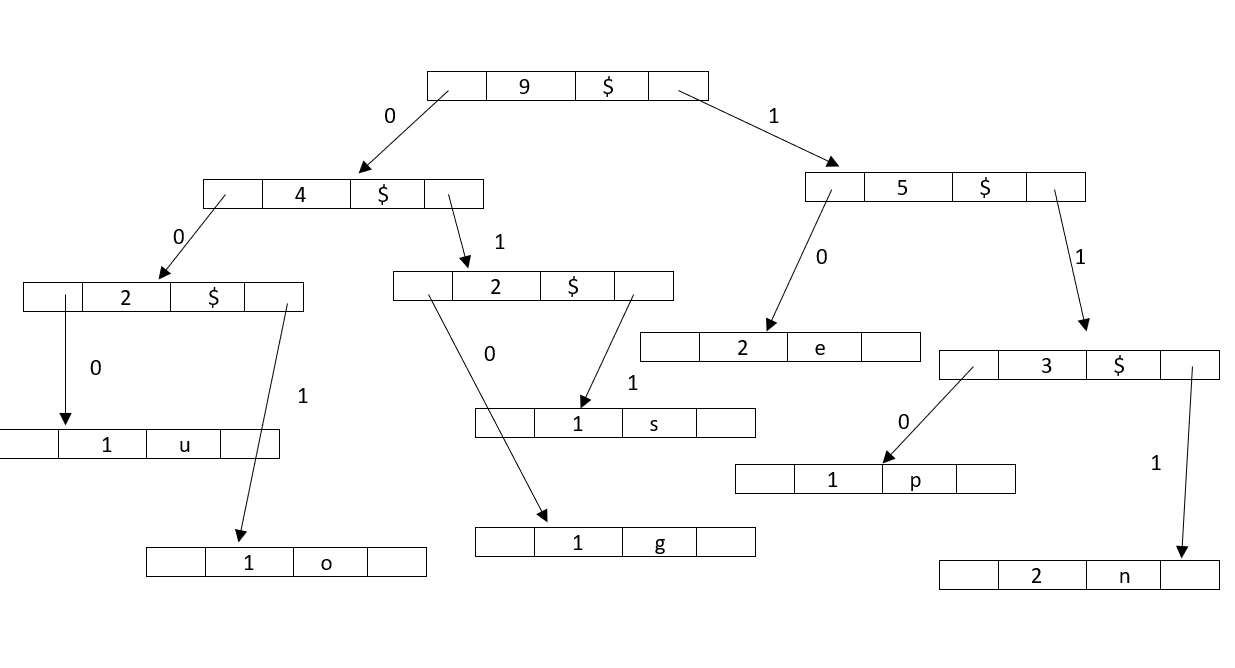
Tree obtained here is:
Another approach
We can achieve Huffman decoding using hashmap also.Steps involved are:
- Store all the codewords in the map and fetch each sub-string in the map.
Time & Space Complexity
Time Complexity of Decoding Step : O(N),where n is the length of the string.
Time Complexity of Encoding Step : O(N logN),where n is the number of unique characters.
Question
Using the above obtained huffman tree,decode the string : 10010001000
Options are:
- open
- genus
- egou
- opge
With this article at OpenGenus, you must have the clear idea of Huffman Decoding. Enjoy.