Im2col stands for Image to Column and is an implementation technique of computing Convolution operation (in Machine Learning) using GEMM operations. This is a preferred way of computing Convolution as GEMM operations from BLAS and BLIS libraries are optimized for specific hardware platforms and performs well in practice.

Table of contents:

1. Introduction to im2col Convolution
2. Steps of im2col
3. Pseudocode (Brute force) of Convolution
4. Step 1: Patch matrix
5. Step 2: Kernel for im2colStep 3: GEMM for im2colAlternatives to im2col

Prerequisite: Convolution Filters

Introduction to im2col Convolution

im2col is a technique to convert the image in such a form such that GEMM calls for dot product can be used to find the final output of Convolution. Multiple such GEMM calls shall be used.

Note: im2col does not improve the time complexity of Convolution.

It improves the real time performance of Convolution as it enables the use of GEMM calls.

The key idea is the transform the image into a "Column" based representation and then, multiple parts of it is processed for convolution with the filter using SGEMM or DGEMM calls for Matrix Multiplication.

The idea of im2col Convolution was first introduced in the research paper titled "High Performance Convolutional Neural Networks for Document Processing" by Kumar Chellapilla, Sidd Puri and Patrice Simard. The authors were associated with Microsoft Research. The paper was published in 2006 and as of 2021, it has 540+ citations.

Steps of im2col

The steps of im2col is as follows:

• Convert input image I of size O(HWC) to a patches matrix of size O(HW(K^2)C)

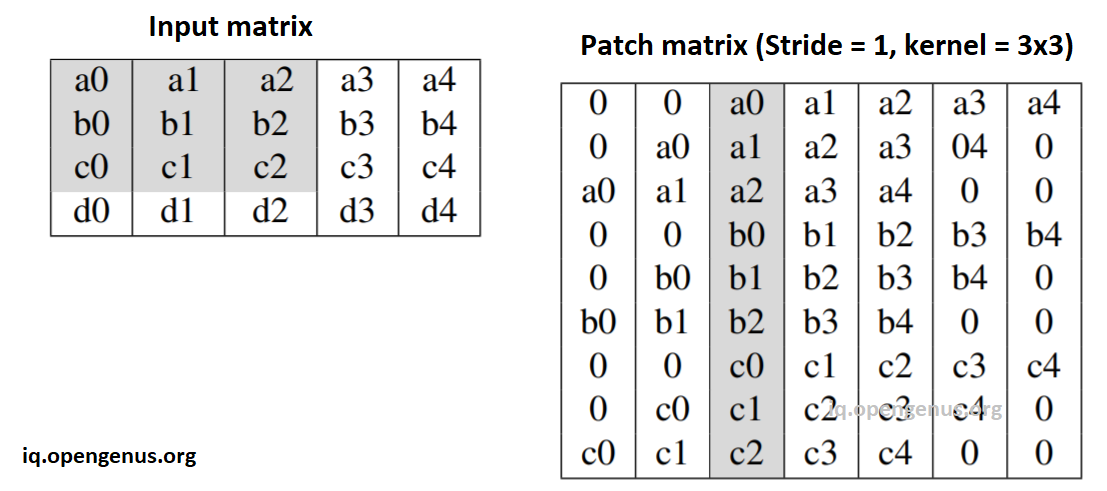
This image illustrates the case of stride=1 and kernel=3x3:

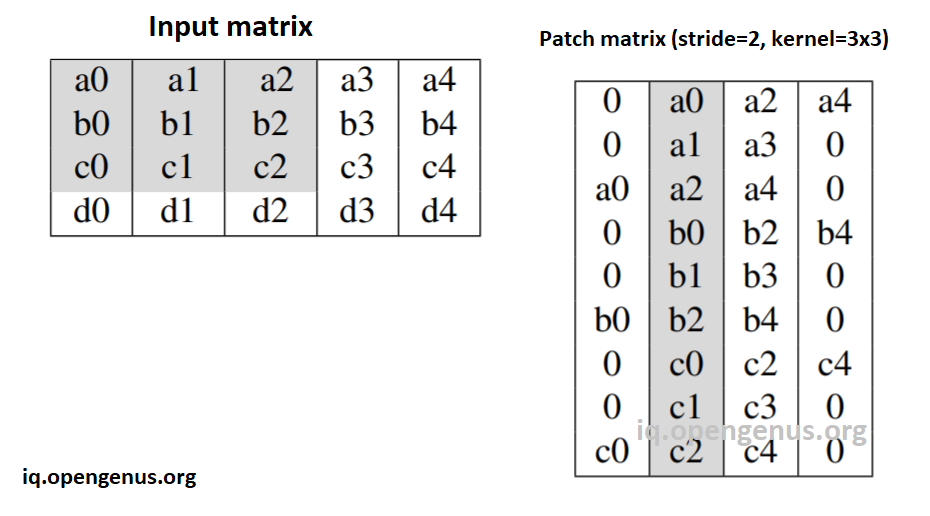
This image illustrates the case of stride=2 and kernel=3x3:

• Convert filter into format Kernel height * kernel width * kernel channel

• Multiply the modified input and filter matrix using GEMM matrix multiplication to get the output. This is a single call.

Pseudocode (Brute force) of Convolution

Following is the pseudocode of the brute force approach:

input[C][H][W];
kernels[M][K][K][C];
output[M][H][W];
for h in 1 to H do
    for w in 1 to W do
        for o in 1 to M do
            sum = 0;
            for x in 1 to K do
                for y in 1 to K do
                    for i in 1 to C do
                    sum += input[i][h+y][w+x] * kernels[o][x][y][i];
         output[o][w][h] = sum;

This will help us understand the difference brought by im2col approach:

Step 1: Patch matrix

We convert an input of size O(HWC) to a patch matrix of O(HW(K^2)C) that is an increase by a factor of O(K^2).

float input[H][W][C];
float patches[H][W][K][K][C];
for ( h = 0; h < H; h++ )
    for ( w = 0; w < W; w++ )
        for ( kh = -K/2; kh < K/2; kh++ )
            for ( kw = -K/2; kw < K/2; kw++ )
                for ( c = 0; c < C; c++ )
                    patches[h][w][kh][kw][c] = input[h+kh][w+kw][c];

Step 2: Kernel for im2col

The format of the kernel should be O(KH * KW * C).

If channel is not the inner most layer, we need to transform it to the above format.

Step 3: GEMM for im2col

GEMM(patches, kernel, output)

output is the Convolution of input and kernel. If kernel is in the correct format, then the temporary space required is O(HW(K^2)C).

Alternatives to im2col

Alternatives to im2col are:

• im2row
• kn2col
• kn2row

In im2row, spatial locality is better compared to im2col and hence, im2row performs better than im2col on CPU. It is interesting to note that im2col performs much better than im2row on GPU.

In kn2row and kn2col, instead of modifying the image, the kernel is modified. This reduces the memory space consumption compared to im2col as kernels are significantly smaller than images.

The best choice depends on different parameters like:

• whether you are using CPU or GPU
• what are the memory limitations of the system
• image and kernel size we are focused on.

Cite this article as:

[Benjamin QoChuk, PhD; OpenGenus team]. 
OpenGenus: im2col Convolution iq.opengenus.org/im2col. 
Information available from iq.opengenus.org.

Revelant research papers:

• "High Performance Convolutional Neural Networks for Document Processing" by Kumar Chellapilla, Sidd Puri and Patrice Simard associated with Microsoft Research.