Convolution Filters / Filters in CNN

Filters in CNN (Convolution Neural Networks) are also known as Convolution Filters. This article will help you understand "What is a filter in a CNN?".

Convolution filters are filters (multi-dimensional data) used in Convolution layer which helps in extracting specific features from input data. There are different types of Filters like Gaussian Blur, Prewitt Filter and many more which we have covered along with basic idea.

Convolution Filter are the tools to derive the best out of images!

Images are fundamentally, matrices.

where each digit, represents the intensity of light in that position.

Above is a grayscale image, that may be represented by one matrice describing the intensity of light.
For a coloured image, this maybe represented by a combination of 3 such matrices, each representing the intensity of red, green and blue, 'their RGB values'.

By varying these values, we bring out relationships and useful information from images. This is done by means of Kernel Convolution.

Kernel Convolution

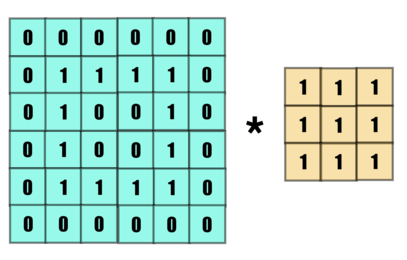
This is a matrice on the left which might represent an image and a smaller matrice on the right, known as the Kernel.
The left matrice is what we are working on, convolving the kernels like the one on the right can help us bring reasonable changes in the image. The operator in between them is representative of the convolution operation.
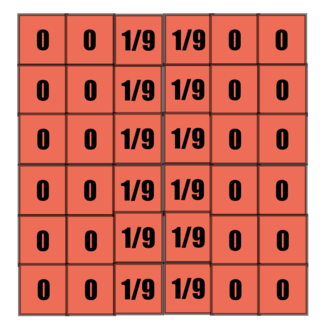
The Size of the kernel in this example is 3x3.

Let us see how convolution is performed.
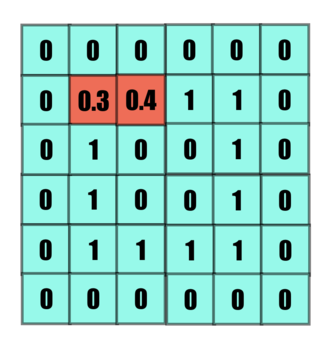
The kernel is overlapped with the image matrice, the overlapping indices are multiplied and added, to replace the value of the central element

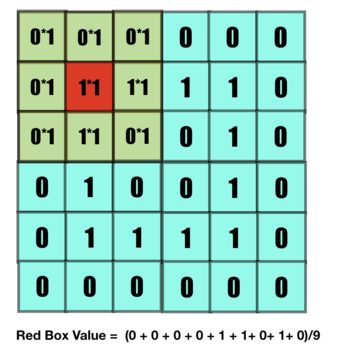
And this way the value of a box is changed according to the kernel. We've divided the sum with the mean for normalization of data, such that input and output shares a similar scale.

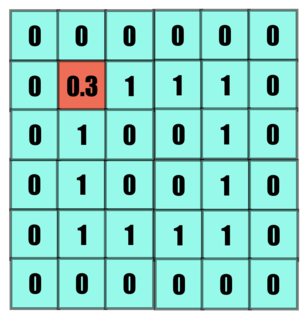
The kernel is then moved forward to bring relevant changes in the subsequent element. Stride is the number of steps it moves, in below example the stride is 1.

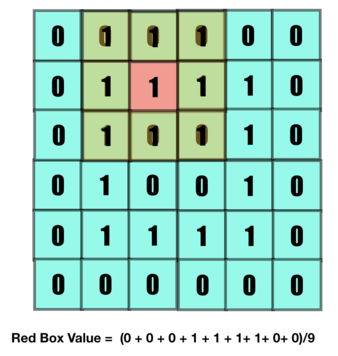
Subsequent value is set.

Following a similar pattern all values are set.

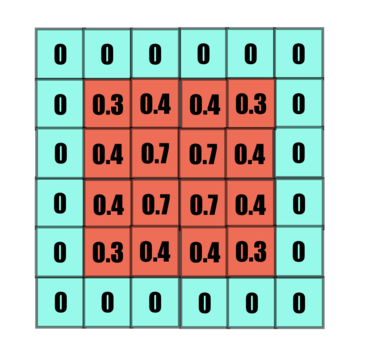
But what about the corners? Here we need Padding, padding virtually extends the matrix to cater to border values as described in the image below. The pink layer isn't a part of the feature matrix, but helps in convolution.
In below example padding is taken as 0.

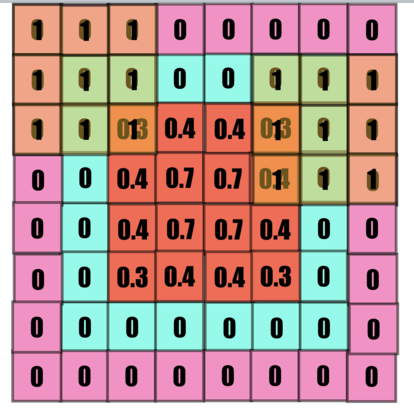
And this is the result of the convolution.

Below is what we created!
You may observe, that the pixel surrounded with darker values, are darker than the pixels surrounded with lighter values. Each pixel is influenced by its neighbours and represent it as a whole.

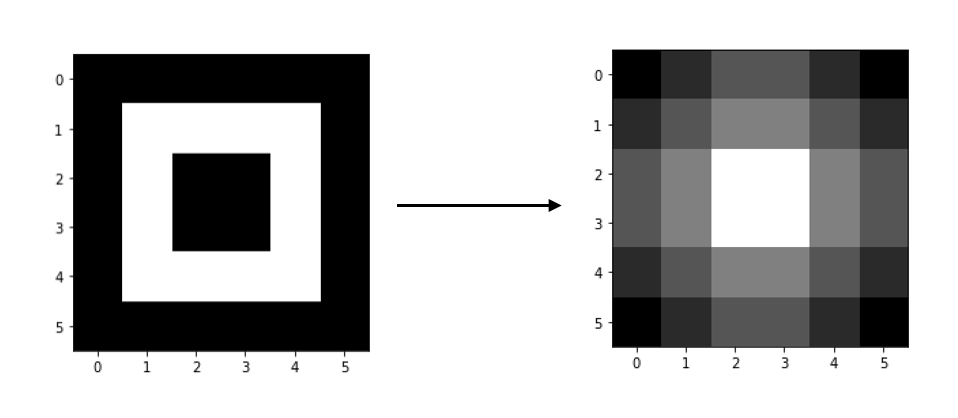
Have a closer look on the kernel, isn't this what we were trying to do? We found the mean of elements encompassed in the kernel. As it picks value from surrounding the difference in element close to each to each other reduces, isn't this called 'blurring'?

Lets make this clearer with an image with greater pixel density.

Above image has been grayscaled and mean blurred to give the image on the right. It is blurred.

You can control the effect of blurring by varying the kernel.

Gaussian Blur

Gaussian Blur is another kernel to blur the image. Below is how the kernel looks like.

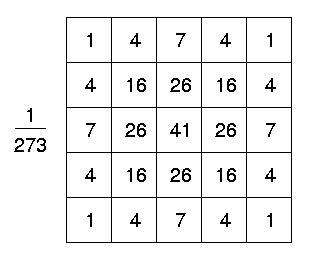
Gaussian blur is popular because of its subtle nature. It feels more controlled, as it is also edge preserving.

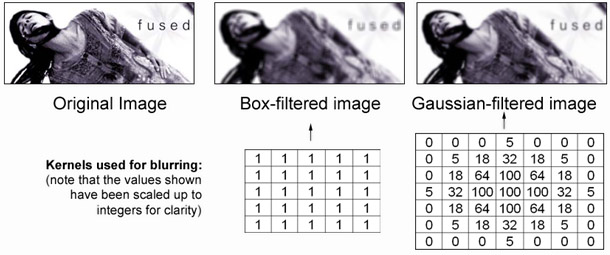
You may observe that the Gaussian blurred image is also blurred, but looks a little bit more meaningful as it appears to be a lot cleaner and understandable while being blurred, in comparison to the mean blurred image.

There are many more operations that can be performed with kernels

Edge Detection (Prewitt filter)

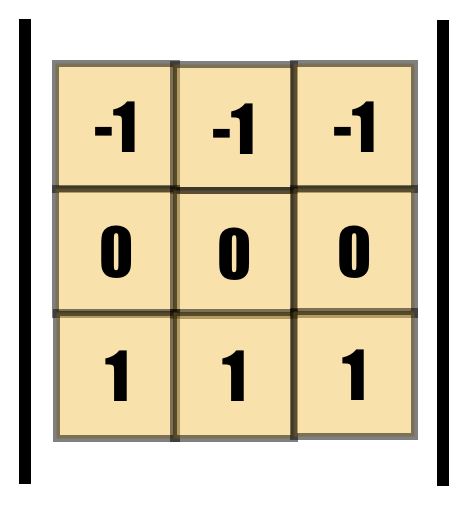
Edges, mark the ends of a figure, they react to sharp changes in intensity. Let us see the example of below 'kernel'.

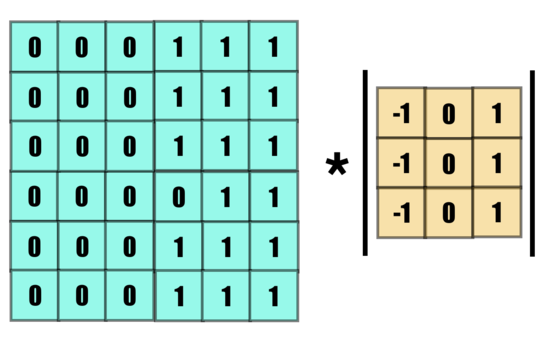
On the left is a very ideal example of an edge, a very sharp change in intensity in between, on the right is our kernel of choice.

Below is our convolution.

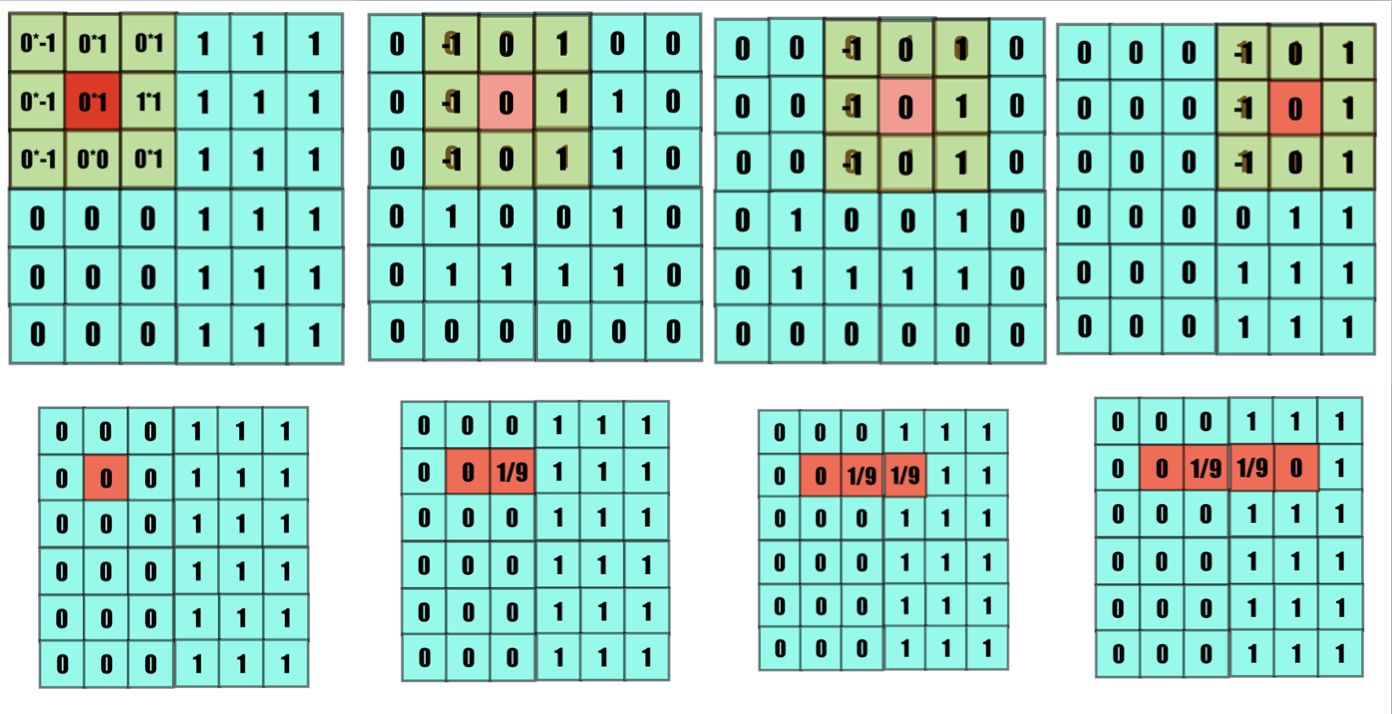
You may observe, that no difference is observed in a constant environment, but there is a sharp increase in intensity when a difference is observed.
That is exactly what we want from our kernel.

This is the result.

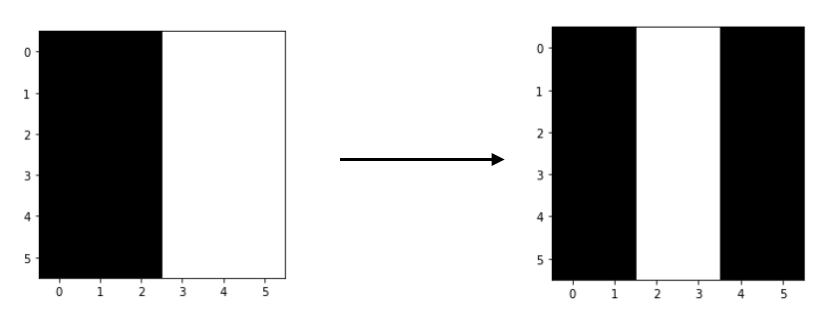
You may observe greater value intensity at the edge, this is exactly what we expected, below is the transformation.

Will this work on a horizontal edge? Try making convolving this kernel on a horizontal edge yourself.
You will realise that the following kernel might seem more appropriate.

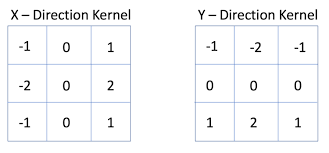
Sobel Filter

It has been observed that the following filter looks more yields better results, this is the Sobel Filter.

This forms images such as the following

To form an image with components of both operators, following method is used.

And this is how edge detection using Sobel Operator is performed, below is an example image.

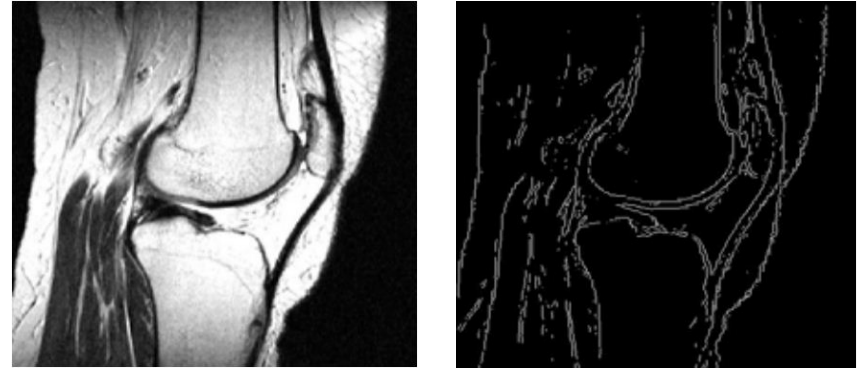
But this seems too noisy with a low resolution or a grainy image like this!

• Noisiness maybe controlled by running a Gaussian Blur before the edge detection, smoothening out the noise. This detector can also be optimised as follows.

Canny Edge Detector

After running the Sobel operator, we perform hysteresis thresholding on it.

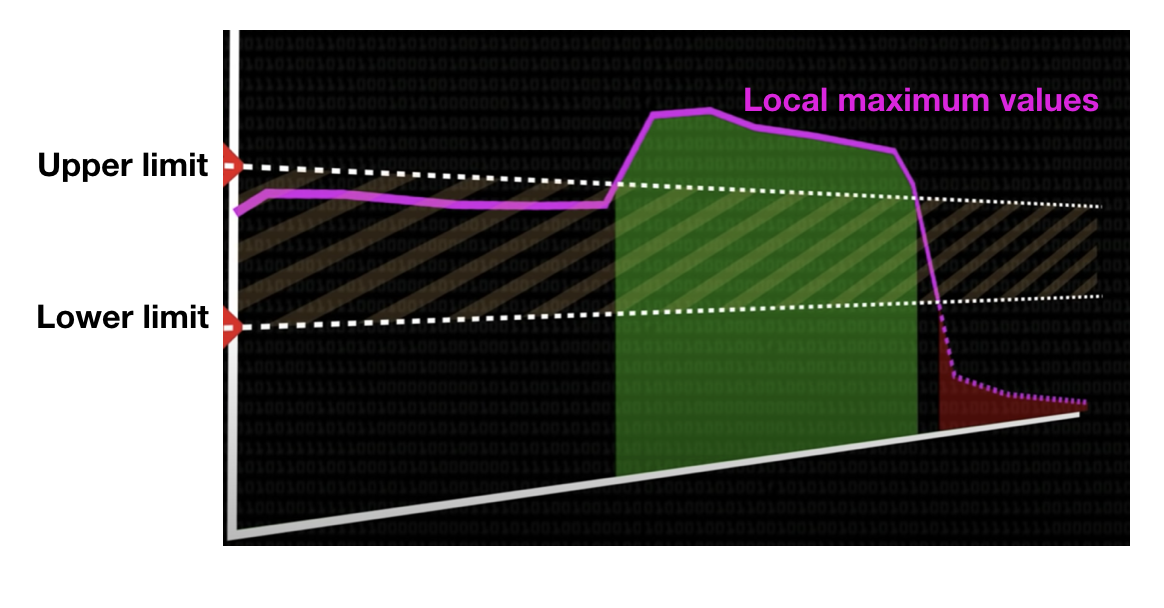
1. Local maximum is detected and plotted as described below.
2. A lower limit and an upper limit is decided.
3. All edges above the upper limit are preserved.
4. All edges above the lower limit and connected to any upper limit edge is preserved.
5. Rest all edges are discarded.

Logic

1. Keeping the local maximum removes noise, as an edge shall not have meaningful edges too close to it.
2. An intensity for the edge must be decided so that only significant edges remain. That is the upper limit.
3. Edges shall not be broken, so edges with relatively lower intensities but connected to the significant edge shall be permitted to a certain extent. That permissible extent is the lower limit.

Below image depicts its effect. The rightmost image is the result of Canny Edge Detector.

You can definitely observe a difference.

So your chain of events maybe
Gaussian Blur -> Sobel Filter -> Canny Edge Detector

There are no rules to it, you are free to explore your paths and bring out the best of an image.
There are a lot of filters to study that perform various operations such as embossing. You could put any values in your kernel and experiment!

Even the filters of your phone are a combination of a lot of such filters at a low level.
Now, start your journey of bringing meaning out of images!

With this article at OpenGenus, you must have the complete idea of Convolution Filters. Enjoy.