
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In the field of data analysis and dimensionality reduction, Non-negative Matrix Factorization (NMF) and Principal Component Analysis (PCA) are two powerful techniques that play an important role in uncovering patterns, reducing noise, and extracting essential features from complex datasets.
Both methods have found applications in various domains, including image processing, text mining, genetics, and more. In this comprehensive exploration, we will delve into the intricacies of NMF and PCA, highlighting their differences, strengths, and unique applications.
Table of contents:
- Non-negative Matrix Factorization (NMF)
- Principal Component Analysis (PCA)
- Difference between NMF and PCA
a. Assumptions and Constraints
b. Applications
c. Interpretability - Beyond NMF and PCA
- Conclusion
Non-negative Matrix Factorization (NMF)
Non-negative Matrix Factorization (NMF) is a matrix factorization technique designed to decompose a non-negative data matrix into two non-negative matrices:
- features matrix (the basis matrix)
- coefficients matrix
The goal of NMF is to approximate the original data matrix by the multiplication of these two non-negative matrices, where the elements are constrained to be non-negative.
In simpler terms, NMF aims to find parts-based, additive representations of the data, which can be particularly useful when dealing with data that inherently exhibits non-negativity, such as images, audio signals, and text.
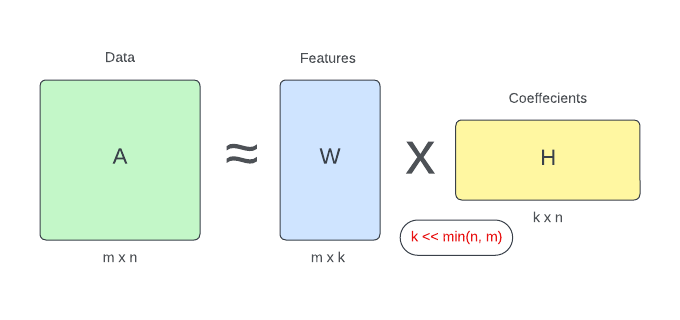
The basic idea behind NMF is that it seeks to uncover the latent structures present in the data by expressing each data point as a combination of underlying patterns represented by the basis matrix. The coefficient matrix then determines the extent to which each of these patterns contributes to reconstructing the original data point.
Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a widely used dimensionality reduction technique that operates by transforming the data into a new coordinate system defined by the principal components. These components are orthogonal axes in the new space that capture the maximum variance in the data.
In essence, PCA aims to find the axes along which the data varies the most, thereby reducing the dimensionality of the dataset while preserving as much of the original variance as possible.
PCA achieves this by computing the eigenvectors and eigenvalues of the covariance matrix of the data. The eigenvectors correspond to the principal components, which are the directions of maximum variance, while the eigenvalues indicate the amount of variance captured by each principal component. By projecting the data onto a subset of these principal components, one can obtain a lower-dimensional representation of the original data, making it easier to analyze and visualize.
Difference between NMF and PCA
While both NMF and PCA are used for dimensionality reduction and feature extraction, they differ in their underlying assumptions, constraints, and applications.
Assumptions and Constraints:
-
Non-negativity Constraint: One of the key distinctions of NMF is the non-negativity constraint on both the basis and coefficient matrices. This constraint makes NMF particularly suited for data that cannot be accurately represented by negative values, such as images and text data.
-
Orthogonality vs. Non-negativity: PCA seeks orthogonal axes (principal components) that maximize variance, while NMF aims to find additive, non-negative combinations of patterns. This difference in constraint leads to the inherent parts-based representations in NMF, as opposed to the uncorrelated representations in PCA.
Applications:
-
NMF Applications: NMF is often favored in scenarios where the data is inherently non-negative and parts-based representations are desired. This includes tasks such as document clustering, topic modeling, and hyperspectral image analysis.
-
PCA Applications: PCA is versatile and widely applicable to various domains. It is commonly used for noise reduction, visualization, and compression. It's particularly useful when there's no clear prior knowledge about the inherent structure of the data.
Interpretability:
-
Interpretability in NMF: The non-negativity constraint in NMF often results in more interpretable representations, as the parts-based nature of the algorithm corresponds well to the nature of the data. This can be advantageous in scenarios where understanding the underlying components is essential.
-
Interpretability in PCA: While PCA provides efficient dimensionality reduction, the principal components may not always correspond to intuitive features in the data. They are linear combinations of the original features and might be harder to interpret directly.
Beyond NMF and PCA
In practice, the choice between NMF and PCA depends on the nature of the data, the goals of the analysis, and the desired outcomes. Furthermore, it's important to note that these two techniques are not mutually exclusive; they can be used in tandem to extract complementary information from the data.
As the field of machine learning and data analysis continues to evolve, variations and hybrid methods that combine the strengths of NMF and PCA have emerged. For instance, Non-negative Matrix Factorization has been extended to incorporate sparsity and hierarchical structures, resulting in Hierarchical Non-negative Matrix Factorization (HNMF). This extension allows for capturing complex patterns in data while retaining the interpretability of parts-based representations.
Conclusion
Non-negative Matrix Factorization (NMF) and Principal Component Analysis (PCA) are two distinct yet powerful techniques for dimensionality reduction and feature extraction. NMF's emphasis on non-negativity and parts-based representations makes it particularly well-suited for data like images and text, while PCA's orthogonality and variance-maximizing nature lend it versatility in various applications. As data scientists and analysts, understanding the nuances and strengths of both NMF and PCA empowers us to choose the most appropriate technique for our specific data and analytical goals. Moreover, the interplay between these techniques and the emergence of hybrid approaches further enrich the landscape of data analysis, opening doors to novel insights and discoveries.
