Table of Contents

1. Key-Takeaways
2. Introduction
3. Making use of convexity in Machine Learning models
4. Why convexity is important in Machine Learning
5. Real life Applications
6. Quiz

Key-takeaways

Convexity is important in ML because:

• Optimization problems have a single global minimum.
• It ensures that any local minimum is also the global minimum.
• It often leads to more robust and stable optimization.
• Optimization algorithms will converge to the optimal solution.
• Convex functions are easier to analyze mathematically.

Introduction

Convexity is a mathematical concept that describes the shape of a mathematical set, such as a curve or a function. In the context of optimization and mathematical analysis, a set is considered convex if, for any two points within the set, the line segment connecting those points also lies entirely within the set.

In simpler terms, a function is convex if, when you draw a straight line connecting any two points on its graph, the line segment lies below or on the graph itself. This is demonstrated by the image below. Convex functions have a distinctive "bowl" shape, and this property has important implications, especially in the field of optimization.

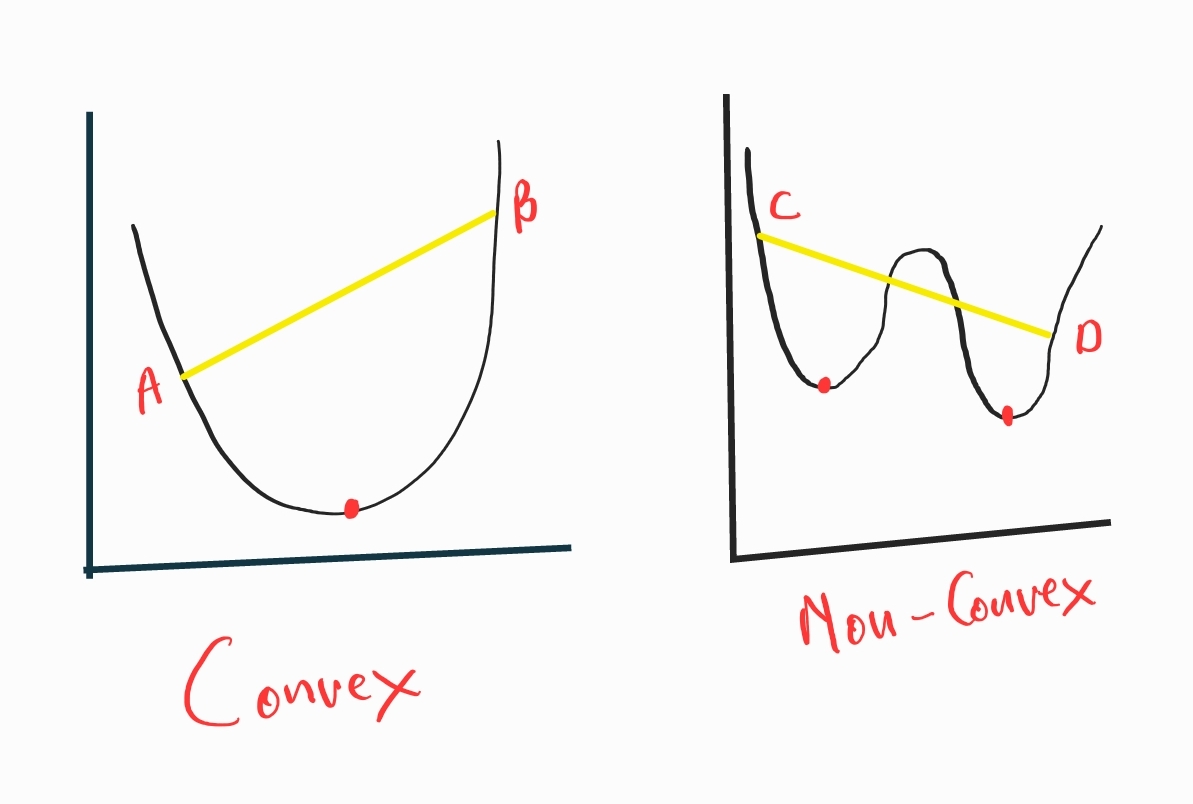
In machine learning, convexity plays a crucial role in optimization problems. Convex optimization problems are desirable because they ensure the existence of a unique global minimum, as show by the image above, making it more feasible to find the optimal solution using various algorithms. Many learning algorithms, such as linear regression and support vector machines, benefit from the use of convex functions and convex optimization, providing stability, 66 convergence guarantees, and efficient computational solutions.

Making use of convexity in Machine Learning models

Suppose you wanted to estimate the price of headphones given their quality and you are given a dataset that consists of the different prices of headphones and their quality. A visual representation of the given data is represented by the graph below. A way in which we can find our estimate is by drawing an approximate straight line that fits our dataset, this linear function is represented by the yellow line below. We can then use the function to find our price represented by the variable p given the quality q.

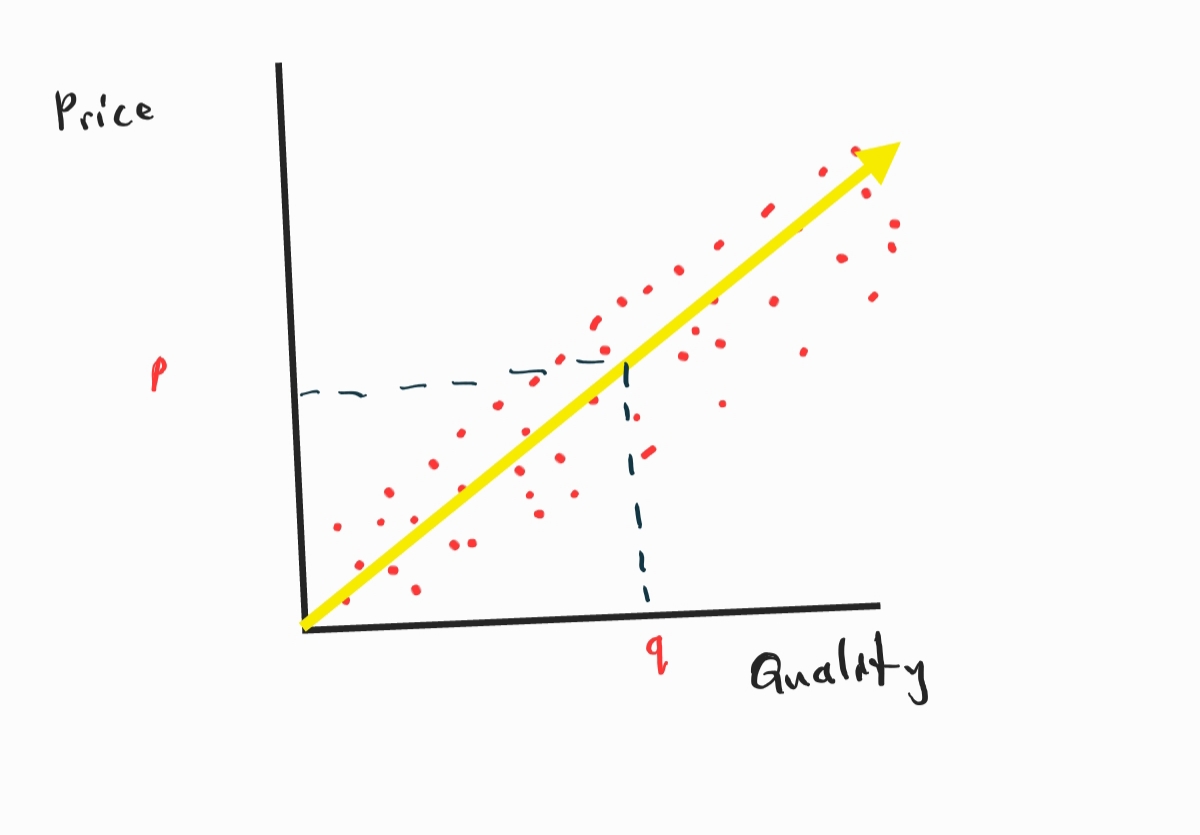
In order to find a function that appropriately fits the dataset, we make use of convexity. Convexity is used because it simplifies the optimization process, provides guarantees of finding globally optimal solutions, and offers efficient algorithms for solving the optimization problem.

To implement convex optimization for fitting a function to a dataset containing the price and quality of headphones in Python, you can use the CVXPY library. CVXPY is a Python library for convex optimization. Here's a simple example assuming a linear relationship between price and quality:

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

Import Libraries: Import the necessary libraries. cvxpy is used for convex optimization, numpy for numerical operations, and matplotlib.pyplot for plotting.

# Generate synthetic data
np.random.seed(42)
num_samples = 100
prices = np.random.uniform(50, 200, num_samples)
quality = 100 - 0.5 * prices + np.random.normal(0, 10, num_samples)

Generate Synthetic Data: Generate synthetic data with a linear relationship between price and quality. The np.random.seed(42) sets the random seed for reproducibility. prices are randomly sampled from a uniform distribution, and quality is created with a linear relationship plus some normally distributed noise.

# Define the variables
a = cp.Variable()
b = cp.Variable()

Define Variables: Define optimization variables a and b, which are the coefficients to be determined by the optimization algorithm.

# Define the objective function (least squares)
objective = cp.Minimize(cp.sum_squares(quality - (a * prices + b)))

Define Objective Function: Formulate the objective function to minimize the sum of squared differences between the predicted quality (a * prices + b) and the actual quality values.

# Define the problem
problem = cp.Problem(objective)

Define Optimization Problem: Create an optimization problem with the defined objective function.

# Solve the problem
problem.solve()

Solve the Problem: Use the solver to find the optimal values for a and b that minimize the objective function.

# Extract the optimal values
optimal_a = a.value
optimal_b = b.value

Extract Optimal Values: Retrieve the optimal values of a and b from the solved optimization problem.

# Print the optimal values
print("Optimal a:", optimal_a)
print("Optimal b:", optimal_b)

Print Optimal Values: Display the optimal values of a and b.

# Plot the data and the fitted line
plt.scatter(prices, quality, label="Data")
plt.plot(prices, optimal_a * prices + optimal_b, color='red', label="Fitted Line")
plt.xlabel("Price")
plt.ylabel("Quality")
plt.legend()
plt.show()

Plot Results: Visualize the synthetic data and the fitted line based on the optimal values of a and b. This helps visualize how well the linear model fits the data.

Make sure to install the CVXPY library before running the code:

pip install cvxpy

This code demonstrates a simple linear regression using convex optimization to find the best-fitting line for the synthetic data. The cvxpy library is used to set up and solve the convex optimization problem. The results are then printed, and a plot is generated to visualize the data and the fitted line.

Let's analyze the time and space complexity of the provided code:

Time Complexity:

Data Generation:
Generating synthetic data involves random sampling, which has a time complexity of O(n), where n is the number of samples.

Convex Optimization:
The time complexity of convex optimization depends on the solver used. Common convex optimization solvers, such as those provided by CVXPY, often have a complexity that scales with the problem size. In the case of linear regression, the typical complexity is O(n^2), where n is the number of variables.

Plotting:
The plotting part has a time complexity proportional to the number of data points, O(n).

Overall, the time complexity is dominated by the convex optimization solver, and it's commonly expressed as O(n^2) for this type of problem.

Space Complexity:

Data Storage:
The space complexity for storing the synthetic data is O(n) since there are two arrays, prices and quality, each with n elements.

Variables:
The space complexity for storing the optimization variables a and b is O(1) as they are just two scalar values.

Objective Function:
The space complexity for the objective function is typically O(n) due to the storage of the residuals.

Optimization Problem:
The space complexity for the optimization problem formulation is O(1) because it involves creating the problem with fixed-size data.

Plotting:
The space complexity for plotting is generally O(1) since it involves creating a fixed number of elements for the plot.

Overall, the space complexity is dominated by the storage of the synthetic data.

Keep in mind that these complexities are approximate and can vary based on the specifics of the data, the optimization problem, and the implementation details of the libraries used.

Why convexity is important in Machine Learning?

Convexity is an important property in machine learning because it simplifies optimization problems and ensures the existence of a global minimum. Here are some key reasons why convexity is valued in ML:

1. Efficient Optimization:

Convex optimization problems have a single global minimum, which makes it easier to find the optimal solution. There are efficient algorithms for solving convex optimization problems, and they are guaranteed to converge to the global minimum.

2. No Local Minima:

In non-convex optimization problems, multiple local minima may exist, making it difficult for optimization algorithms to converge to the global minimum. Convex functions, on the other hand, have no local minima other than the global minimum.

3. Global Optimal Solution:

Convexity ensures that any local minimum is also the global minimum. This property is essential in machine learning applications where finding the best model parameters is crucial for performance.

4. Robustness:

Convexity often leads to more robust and stable optimization. Small changes in the input or the optimization procedure are less likely to lead to large changes in the solution.

5. Convergence Guarantee:

Convex optimization problems have well-established convergence guarantees. This means that iterative optimization algorithms will converge to the optimal solution, and the convergence behavior can be analyzed and predicted.

6. Simplicity of Analysis:

Convex functions are easier to analyze mathematically. This simplicity facilitates the study of convergence properties, uniqueness of solutions, and other aspects of optimization, making it easier for researchers and practitioners to understand and work with the models.

7. Regularization:

In machine learning, regularization techniques (such as L1 and L2 regularization) are often used to prevent overfitting and promote simpler models. Many regularization terms are convex, ensuring that the overall optimization problem remains convex.

8. Linear Programming:

Many real-world problems can be formulated as convex optimization problems. Linear programming, a special case of convex optimization, is widely used in machine learning for tasks like support vector machines (SVMs) and linear regression.

While convexity simplifies optimization, it's important to note that not all machine learning problems are convex. Convexity is often a desirable property, but researchers and practitioners have also developed methods to deal with non-convex optimization problems, although they may be more challenging to solve and may require additional considerations and techniques.

Real life Applications

Convexity plays a crucial role in various aspects of machine learning, contributing to both the theoretical foundations and practical algorithms. Here are some real-life applications of convexity in machine learning:

1. Optimization Algorithms:

Gradient Descent: Convexity ensures that gradient descent always converges to the global minimum, making it a popular optimization algorithm for convex loss functions.
Stochastic Gradient Descent (SGD): In the context of large-scale machine learning, SGD benefits from convexity as it converges efficiently even with noisy or stochastic gradients.

2. Linear Regression:

The least squares objective function in linear regression is convex. This property ensures that the optimization problem has a unique global minimum, and algorithms like gradient descent converge reliably.

3. Support Vector Machines (SVM):

SVM aims to find the hyperplane that maximally separates data points of different classes. The optimization problem associated with SVM involves convex quadratic programming, making it computationally efficient.

4. Logistic Regression:

The logistic loss function used in logistic regression is convex. This property ensures that optimization algorithms converge to a global minimum, making logistic regression a popular choice for binary classification.

5. L1 and L2 Regularization:

Regularization terms, such as L1 (Lasso) and L2 (Ridge), are often added to machine learning models to prevent overfitting. Both L1 and L2 regularization lead to convex optimization problems.

6. Convex Neural Networks:

Certain neural network architectures and loss functions are designed to be convex. Convex neural networks have been studied for their optimization properties, allowing for more predictable and stable training.

7. Principal Component Analysis (PCA):

PCA involves finding the principal components of a dataset, and the associated optimization problem is convex. Convexity ensures that the algorithm converges to a global optimum.

8. Matrix Factorization:

Convex optimization is used in matrix factorization problems, such as collaborative filtering in recommendation systems. Convex formulations help in efficiently factorizing matrices into lower-rank approximations.

9. Portfolio Optimization:

In finance, convex optimization is applied to portfolio optimization problems. This involves finding the allocation of assets that maximizes returns while minimizing risk, subject to certain constraints.

10. Structured Prediction:

In tasks like sequence labeling or parsing, where the output space has a structured format, convex relaxations can be employed to formulate efficient optimization problems.

Understanding and leveraging convexity in these applications not only facilitates efficient optimization but also provides guarantees on the convergence and optimality of the solutions, making machine learning models more reliable and interpretable.

Quiz