Markov Chain Neural Network (MCNN)

In this OpenGenus article, we will explore Markov chains, their intersections with neural networks, and a simple implementation of a Markov chain neural network (MCNN). We will also take a look at their applications.

Table of contents:

1. What are Markov Chains?
2. What are Neural Networks?
3. A Markov Chain Neural Network
4. Implementation
5. Applications of Markov Chain Neural Network
6. Key Takeaways

What are Markov Chains?

A Markov chain is a random model conveying a sequence of possible events and their transitions. The probability of each event occurring or state being reached depends on the previous state or event. Simply put, Markov models represent a system of change that is based on the assumption that future states depend solely on the current state. This property of Markov chains makes it useful for predictive modeling, ranging from predicting weather patterns to stock market movements.

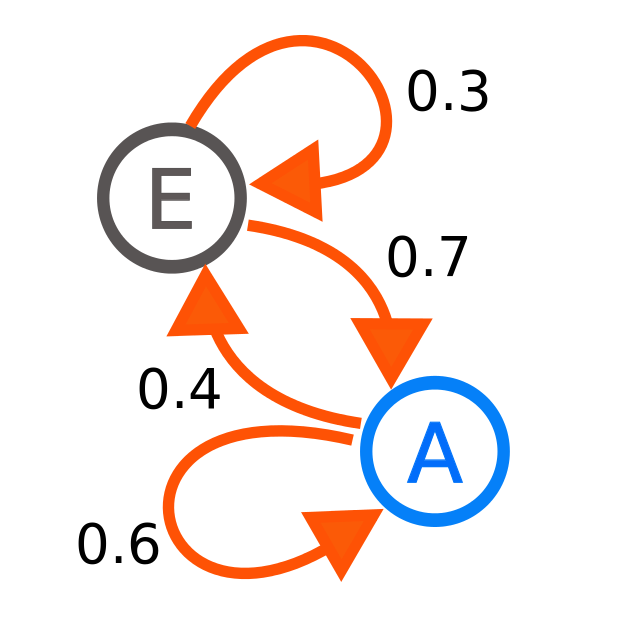
Above is an example of a Markov chain modeled using a Directed Graph where each arrow's weight represents the probability of transitioning from current state to another state.

What are Neural Networks?

Neural networks are a method of machine learning inspired by the inner workings of the human brain. They consist of neurons (nodes) connected together in a layered structure. The neural network created can process and learn from data, detect patterns, etc. The complex and versatile nature of neural networks allows them to be applied in numerous fields, including but not limited to natural language processing, image recognition, and the construction of highly competent AI capable of defeating humans in games like chess and go.

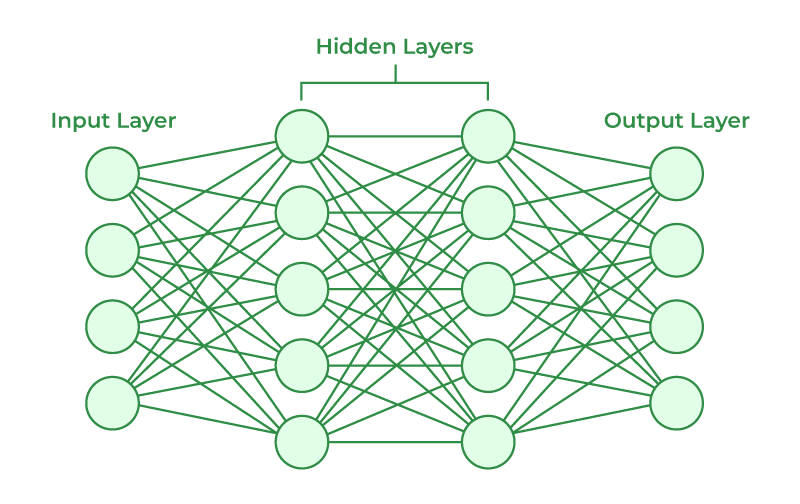
Above is an illustration of the architecture of a neural network. The input and output layers behave as suggested by their names, and the hidden layers are responsible for learning the intricate patterns and structures in the data passed in and making the neural network "deep." Each neuron in the hidden layer multiplies inputs received by its weights and sends them through an activation function and onto the next neuron in the layer. The "black-box" nature of the hidden layer makes it difficult to trace its activity, especially in deeper neural networks.

A Markov Chain Neural Network

Normal neural networks with their hidden layer architecture, once trained with sample data, will tend to behave in a deterministic fashion and always provide the same answer or output for a given input. This results in non-random and robotic behavior, easily observable in video games with predictable enemy AI behavior or language models that regurgitate the same answer for similar prompts.

The convergence between Markov chains and neural networks serves as a method to bring randomness to neural networks to produce human-like behavior. The neural network architecture can be modified to emulate Markov chains and their stochastic behavior by making a simple change: adding an additional random variable input node. This random variable parameter will be used as a switch node by the hidden layers to produce different outcomes each time, adding an element of unpredictability to the output of the network. Below is an illustration of the Markov Chain Neural Network architecture implemented by Maren Awiszus and Bodo Rosenhahn.

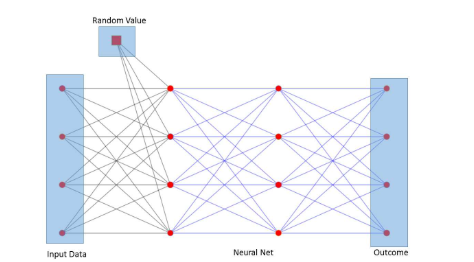
Image source: https://openaccess.thecvf.com/content_cvpr_2018_workshops/papers/w42/Awiszus_Markov_Chain_Neural_CVPR_2018_paper.pdf

Implementation

We can represent a simplified implementation of a neural network that behaves like a Markov chain in Python.

class NeuralNetwork:
    def __init__(self, learning_rate):
        # Add an additional weight for the random input node
        self.weights = np.array([np.random.randn(), np.random.randn(), np.random.randn()])
        self.bias = np.random.randn()
        self.learning_rate = learning_rate

    def _sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def _sigmoid_deriv(self, x):
        return self._sigmoid(x) * (1 - self._sigmoid(x))

    def predict(self, input_vector, random_input):
        # Append the random input to the input vector
        extended_input = np.append(input_vector, random_input)
        layer_1 = np.dot(extended_input, self.weights) + self.bias
        layer_2 = self._sigmoid(layer_1)
        prediction = layer_2
        return prediction

    def _compute_gradients(self, input_vector, random_input, target):
        # Append the random input to the input vector
        extended_input = np.append(input_vector, random_input)
        layer_1 = np.dot(extended_input, self.weights) + self.bias
        layer_2 = self._sigmoid(layer_1)
        prediction = layer_2

        derror_dprediction = 2 * (prediction - target)
        dprediction_dlayer1 = self._sigmoid_deriv(layer_1)
        dlayer1_dbias = 1
        dlayer1_dweights = (0 * self.weights) + (1 * extended_input)  # Adjust this computation to include the extended input

        derror_dbias = (
            derror_dprediction * dprediction_dlayer1 * dlayer1_dbias
        )
        derror_dweights = (
            derror_dprediction * dprediction_dlayer1 * dlayer1_dweights
        )

        return derror_dbias, derror_dweights

If you inspect the code closely, you will notice the random_input parameter in the predict() and compute_gradients() functions. Each time these functions are called, a random variable is computed and passed in which brings the stochastic property of Markov models into the predictions and computations of our Neural Network. This random variable affects the outputs of our network and creates the randomness mentioned earlier.

Applications of Markov Chain Neural Network

A Markov chain network, with its property of outputting somewhat random results, can allow for more human-like AI in video games, ambiguous image completion or less robotic language models and chat bots. Below is an illustrated use case where the Markov chain network was used to complete a partial image passed as input, along with a random variable.

Image source: https://openaccess.thecvf.com/content_cvpr_2018_workshops/papers/w42/Awiszus_Markov_Chain_Neural_CVPR_2018_paper.pdf

Key Takeaways

• Markov chains are state transition models that follow a stochastic/random property such that the probability of each state being reached depends on the previous state.
• Neural networks are a method of machine learning, modeled after our brains, containing an input, hidden and output layer of interconnected neurons which process and learn data. Neural networks are deterministic.
• To exhibit unpredictable or random behavior from a neural network, it can be modeled to emulate a Markov chain by adding a random variable input node.
• Markov chain networks can be used to emulate more natural behavior in video games, language models, etc.