Machine Learning Interview Questions [GOAT 🐐]
In this article, we have presented Multiple Choice Questions (MCQs) in Machine Learning with a focus on Interviews. Each questions has been provided the correct answer along with detailed explanation.
In this, we have covered basic Machine Learning topics such as:
- Supervised, Unsupervised and Semi-Supervised Learning
- Naive Bayes, Central Limit Theorem, Regularization, Standardization, Normalization, Overfiting, Underfiting, Gradient descent, Backpropagation, K nearest neighbor algorithm
- Distance metrics, Clustering
Q1. Which one of the following does not use Labeled Data for Training?
a) Supervised Learning
b) Unsupervised Learning
c) Semi-Supervised Learning
Answer: b) Unsupervised Learning
Unsupervised Learning use only Unlabeled data for Training. In short, the idea is as follows:
- Supervised Learning: Labeled Data only
- Unsupervised Learning: Unlabeled Data only
- Semi-Supervised Learning: Combination of Labeled and Unlabeled Data
Q2. Supervised Learning is classified as Regression and Classification. Which one of the following is an example of Classification?
a) Linear Regression
b) Polynomial Regression
c) Logistic Regression
d) Non Linear Regression
Answer: c) Logistic Regression
In Logistic Regression, the answer is either 0 or 1. Hence, it is used for Classification. The other types are examples of Regression.
Supervised Learning is of two types:
- Regression
- Classification
Regression include techniques like:
- Linear Regression
- Bayesian Linear Regression
- Polynomial Regression
- Regression Trees
Classification include techniques like:
- Decision Tree
- Random Forest
- Logistic Regression
- Support Vector Machine
Q3. Like Supervised Learning, Unsupervised Learning is of two types as well. What are the two types?
a) Regression
b) Clustering
c) Composition
d) Association
Answer: b) Clustering and d) Association
Unsupervised Learning is of two types:
- Clustering
- Association
Clustering is the technique of grouping data while Association is the technique of finding relation between variables in a dataset (for Recommendation applications).
Q4. Which one of the following is an example of Semi-Supervised Learning?
a) Linear Regression
b) Logistic Regression
c) K means Clustering
d) Generative Adversarial Network (GAN)
Answer: d. Generative Adversarial Network (GAN)
Semi-Supervised Learning is a technique that makes use of both Labeled and Unlabeled data. GAN is an example of Semi-Supervised Learning.
In fact, GAN can be used as Unsupervised, Semi-Supervised and Fully-Supervised Learning. GAN models are used to generate a new set of data based on the input data. In constrast, Linear and Logistic Regression can be used as Supervised Learning only while K means Clustering is used as Unsupervised Learning.
Q5. Standard ML applications like Image Recognition is an example of?
a) Supervised Learning
b) Unsupervised Learning
c) Semi-Supervised Learning
Answer: a) Supervised Learning
Standard ML applications like Image Recognition require trained models like ResNet50 which are examples of Supervised Learning as the training data are labeled.
Q6. In Naive Bayes classifier equation, what is P(A|B)?
a) Likelihood of evidence given hypothesis is true
b) Posterior probability of hypothesis given evidence is true
c) Prior probability of hypothesis
d) Prior probability that evidence is true
Answer: b) Posterior probability of hypothesis given evidence is true
Naive Bayes classifier equation is as follows:
P(A|B) = P(B|A) P(A) / P(B)
The different terms are as follows:
- Likelihood of evidence given hypothesis is true: P(B|A)
- Posterior probability of hypothesis given evidence is true: P(A|B)
- Prior probability of hypothesis: P(A)
- Prior probability that evidence is true: P(B)
Q7. Naive Bayes classifier is an example of?
a) Low Bias, Low Variance
b) High Bias, Low Variance
c) Low Bias, High Variance
d) High Bias, High Variance
Answer: b) High Bias, Low Variance
Naive Bayes classifier is an example of High Bias, Low Variance.
If the training data is small and the number of features is high, then High Bias and Low Variance algorithms are used. Examples include Linear SVM and Naive Bayes classifier.
If training data is large, then Low Bias and High Variance algorithm is used such as K Nearest neighbors, Decision Tree, Randoma forest.
Q8. In Central Limit Theorem, as data size becomes large, the distribution becomes?
a) Poisson Distribution
b) Binomial Distribution
c) Normal distribution
d) Cannot be determined
Answer: c) Normal distribution
Central Limit Theorem states that as data size becomes large, the distribution of the data becomes Normal distribution.
In other terms, if the sample data is large, then the mean of the sample data will be very close to the actual mean of the entire data set.
Q9. How many types of Regularization techniques are there?
a) 4
b) 6
c) 10
d) 2
Answer: d) 2
There are two types of Regularization namely:
- L1 Regularization (Lasso)
- L2 Regularization (Ridge)
Q10. The difference in L1 and L2 Regularization is in?
a) Beta term
b) Lambda
c) Penalty term
d) Loss function
Answer: c) Penalty term
The difference in L1 and L2 Regularization is in Penalty term.
Following is the equation of L1 Regularization:
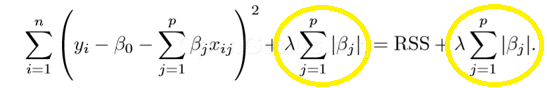
Following is the equation of L2 Regularization:
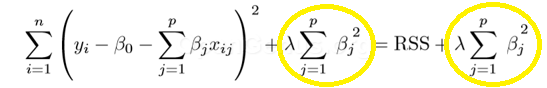
Learn more about L1 and L2 Regularization.
Q11. To prevent Overfitting, data is split into how many parts?
a) 2
b) 3
c) 4
d) 5
Answer: b) 3
Overfitting is the problem where a model learn the low level features more accurately compared to high level features of the training data. Due to this, the trained model performs with near 100% accuracy for training data but low accuracy for other dataset.
To prevent Overfitting, one approach is to split the data into 3 parts namely:
- Training set
- Cross validation
- Test set
Q12. If a model is trained using K nearest neighbor algorithm, underfiting will most likely happen for which value of K?
a) 1
b) 2
c) 5
d) 20
Answer: d) 20
Larger the value of K, the more likely underfiting will take place.
Similarly, the smaller the value of K, the more likely overfiting will take place.
Hence, it is very important to use the correct value of K in K nearest neighbor algorithm and this is a challenge as well.
Q13. Among the two, which one is more likely to result in underfiting?
a) Decision tree
b) Decision stump
Answer: b) Decision stump
As a rule, Decision stump is more likely to result in underfiting while Decision tree is more likely to result in overfiting. Hence, the behavior of both is opposite with respect to overfiting and underfiting.
Q14. In case of overfiting, the training error is ______ compared to test error?
a) Less
b) Equal
c) Greater
Answer: a) Less
In case of overfiting, the model is well versed with the training dataset and hence, the error is least in case of training dataset. Therefore, the training error is less compared to test error.
Ideally, models should be training such that:
- train error is as close as test error as possible
- error should be minimal
Q15. In case of overfiting, the model will most likely have?
a) High variance
b) High bias
Answer: a) High variance
Overfiting results in high variance while underfiting results in High bias.
Q16. Gradient descent is an optimization algorithm to find local minimum of a differentiable function. Gradient descent take steps in ______ direction of gradient?
a) Positive
b) Negative
c) Maximum change
Answer: b) Negative
Gradient descent take steps in negative direction of gradient. This enables Gradient descent to take a steep descent and reach the local minimum.
Q17. Which one of the following is computationally fastest?
a) Batch gradient descent
b) Mini-batch gradient descent
c) Stochastic gradient descent
Answer: c) Stochastic gradient descent
The idea is as follows:
- Batch gradient descent consider the entire dataset to take a single step
- Mini-batch gradient descent considers a small batch from the dataset to take a single step
- Stochastic gradient descent considers only one data point to take a single step
Q18. When no hyper-parameter is present, which one will you use?
a) Stochastic gradient descent
b) Ordinary Least Squares
Answer: b) Ordinary Least Squares
Ordinary Least Squares does not require hyper-parameters but Stochastic gradient descent do. This differences are:
- Time Complexity of Stochastic gradient descent is O(K * N^2) while for Ordinary Least Squares, it is O(N^3).
- Stochastic gradient descent require hyper-parameters but Ordinary Least Squares do not.
- Stochastic gradient descent need to iterate but Ordinary Least Squares do not.
Q19. Momentum gradient descent is used over Stochastic and mini-batch gradient descent to overcome a specific problem. What is the problem?
a) Oscillation
b) Non-linear
c) Learning rate
Answer: a) Oscillation
Oscillation is the problem that parameter of a model is updated with every step but the direction of update involve some variance in gradient steps. To overcome oscillation, Momentum gradient descent is used over Stochastic and mini-batch gradient descent.
Q20. Gradient descent can be applied on both convex and non-convex function. What is the main feature of non-convex function?
a) Only one minimum value
b) More than one minimum value
c) Monotonic increasing function
d) Monotonic decreasing function
Answer: b) More than one minimum value
Convex function has only one minimum value which is the global minimum but in case of non-convex function, there are multiple minimum value so there are many local minima and one global minima.
Q21. Perceptron is an example of?
a) Association
b) Binary classifier
c) Clustering
Answer: b) Binary classifier
Perceptron is an example of Binary classifier which is a type of Supervised learning.
Q22. What are the limitations of Backpropagation?
a) Slow convergence
b) Scaling
c) Local minima problem
d) Oscillation
Answer: a, b, c
The limitations of Backpropagation are:
- Slow convergence
- Scaling
- Local minima problem
Q23. How does learning is stopped in Backpropagation?
a) Learning rate
b) Gradient value
c) Heuristic condition
Answer: b) Gradient value
In case of Backpropagation, learning process is stopped where the average value of gradient goes below a certain threshold value.
Q24. Which algorithm is used in Backpropagation?
a) Gradient descent
b) Activation function
c) Naive Bayes classifier
Answer: a) Gradient descent
Gradient descent is used in Backpropagation. Backpropagation is the most important operation for training a Machine Learning model and Gradient descent helps in reaching minima to minimize training error.
This is a computational expensive operation. This was the reason why Machine Learning was not popular in 1980s despite the fact that the field was mature theoretically. In 2010s, with the introduction of powerful computing devices, Machine Learning became feasible and took a big leap.
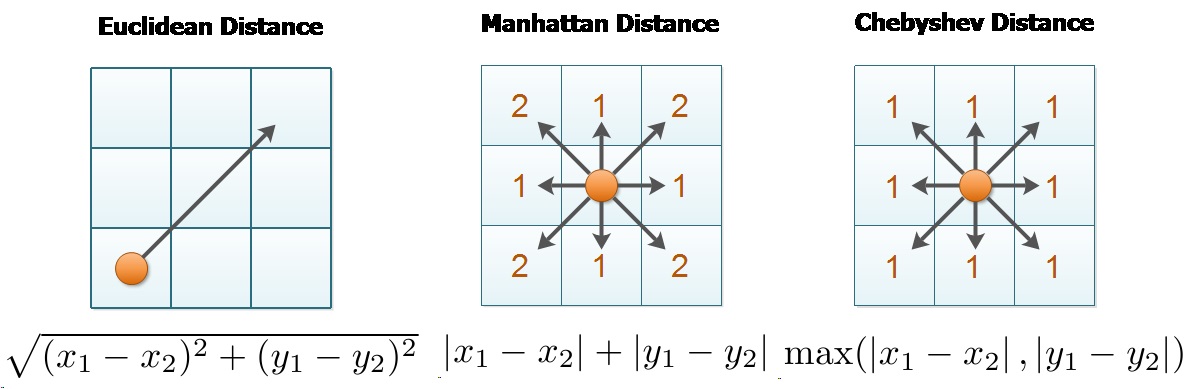
Q25. Which one of the following distance metric is used for categorical variable in K nearest neighbor algorithm?
a) Manhattan distance
b) Euclidean distance
c) Hamming distance
Answer: c) Hamming distance
Hamming distance is used for categorical data while the other two metrics namely Manhattan and Euclidean distance are used for continuous data.
Q26. In K nearest neighbor algorithm, the value of K is choosen where?
a) Distance between clusters in maximized
b) Validation error is minimum
c) Based on experimentation
Answer: b) Validation error is minimum
In K nearest neighbor algorithm, the value of K is choosen where Validation error is minimum. This improves the accuracy of the algorithm.
Q27. Which of the following can be used to predict missing values in continuous and categorical data?
a) Linear regression
b) Polynomial regression
c) K nearest neighbor
Answer: c) K nearest neighbor
K nearest neighbor is used with both continuous and categorical data whereas Regression techniques work with continuous data only. All three techniques can be used to predict missing values in the data they are applied on.
Q28. Euclidean distance is a special case of?
a) Manhattan distance
b) Chebyshev Distance
c) Minkowski distance
Answer: c) Minkowski distance
Euclidean distance is a special case of Minkowski distance where p = 2. Furthermore, Manhattan distance is also a special case of Minkowski distance where p = 1.
Consider two points P1 and P2:
P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)
Then, the Minkowski distance between P1 and P2 is given as:
Distance = [(X1-Y1)^P + (X2-Y2)^2 + ... + (XN-YN)]^(1/P)
With P = 2, we get Euclidean distance.
With P = 1, we get Manhattan distance.
Q29. What will be the Euclidean distance between two points (1, 2) and (5, 5)?
a) 7
b) 5
c) 1
d) 4
Answer: b) 5
Euclidean distance = [(x1 - x2)^2 + (y1 - y2)^2]^0.5
So, the calculation is as follows:
[(1-5)^2 + (2-5)^2]^0.5
= [(-4)^2 + (-3)^2]^0.5
= [16+9]^0.5
= 25^0.5
= 5
Q30. What will be the Manhattan distance between two points (1, 2) and (5, 5)?
a) 7
b) 5
c) 1
d) 4
Answer: a) 7
Manhattan distance = [|x1 - x2| + |y1 - y2|]
where |x| is mod of x.
So, the calculation is as follows:
[|1-5| + |2-5|]
= [|-4| + |-3|]^
= [4 + 3]
= 7
Q31. What will be the Chebyshev distance between two points (1, 2) and (5, 5)?
a) 7
b) 5
c) 1
d) 4
Answer: d) 4
Chebyshev Distance = Maximum(|x1 - x2|, |y1 - y2|)
So, the calculation is as follows:
Maximum(|1-5|, |2-5|)
= Maximum(|-4|, |-3|)
= Maximum(4, 3)
= 4
This image summarizes the distance metrics:
Q32. Clustering is a type of?
a) Supervised
b) Unsupervised
Answer: b) Unsupervised
Clustering is the technique of grouping data and hence, does not require labeled data. In fact, clustering is one of the two types of Unsupervised Learning. Unsupervised Learning is of two types:
- Clustering
- Association
Q33. What is the minimum number of features required for Clustering?
a) 0
b) 1
c) 2
d) 3
Answer: b) 1
The minimum number of features required for Clustering is 1. The data is clustered based on the input feature.
Q34. Does the output of K means Clustering remain same across different runs?
a) Yes
b) No
Answer: b) No
The output of K means Clustering vary across different runs. This is because K means Clustering go to a local minima and not the global minima. Due to this, it can land to different local minima for each run.
Q35. Which clustering algorithm have the problem of convergence at local optima?
a) K means clustering algorithm
b) Diverse clustering algorithm
c) Agglomerative clustering algorithm
d) Expectation Maximization clustering algorithm
Answer: a) K means clustering algorithm, d) Expectation Maximization clustering algorithm
Only two clustering algorithms have the problem of convergence at local optima. These are K means clustering algorithm and Expectation Maximization clustering algorithm.
Q36. Which Clustering algorithm has the problem of outlier?
a) K medoids clustering algorithm
b) K means clustering algorithm
c) K medians clustering algorithm
d) K modes clustering algorithm
Answer: b) K means clustering algorithm
Only K means clustering algorithm has the problem of outlier. This is because it considers the mean of data points of a cluster.
Q37. In this graph of Silhouette coefficient vs Number of clusters, which one of the best number of clusters?
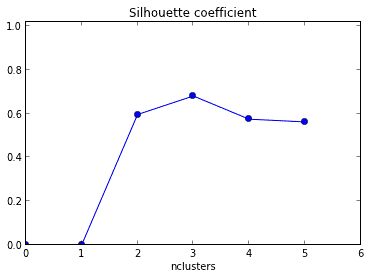
a) 2
b) 3
c) 4
d) 5
Answer: b) 3
Silhouette coefficient is a metric of how similar an object is to its own cluster compared to other clusters. Higher the Silhouette coefficient, the better is the clustering.
For the number of clusters = 3, Silhouette coefficient is the highest and hence, it is the best number of clusters.
Q38. Which one is an iterative technique to handle missing values before Clustering Analysis?
a) Imputation with mean
b) Nearest Neighbor assignment
c) Imputation with median
d) Imputation with Expectation Maximization algorithm
Answer: d) Imputation with Expectation Maximization algorithm
All the four techniques can be used to handle missing values before Clustering Analysis but only one technique namely "Imputation with Expectation Maximization algorithm" is an iterative technique.
Q39. F-Score is used to measure Clustering result. What is the range of F-Score?
a) [0, 100]
b) [-1, 1]
c) [0, 1]
d) All possible values
Answer: c) [0, 1]
F-Score value can range from 0 to 1.
- 1 denotes correct cluster has been assigned.
- 0 denotes that the value of precession and recall is 0
Q40. What one of the Clustering algorithm involve a Merging step?
a) K means clustering
b) Mean Shift Clustering Algorithm
c) Hierarchical Clustering
d) DBSCAN Clustering Algorithm
Answer: c) Hierarchical Clustering
Hierarchical Clustering involve merging as the last step while forming clusters. If iteration is not stopped, then only one cluster remain at the end.
Q41. K means algorithm is non-deterministic. Hierarchical Clustering is?
a) Deterministic
b) Non-deterministic
Answer: a) Deterministic
Unlike K means clustering algorithm, Hierarchical Clustering is a deterministic clustering technique that is the result remain the same across different iterations.
Q42. What is the method called which is used to measure distance between two clusters?
a) Linkage method
b) Distance metric
c) F-Score
Answer: a) Linkage method
There are many ways to determine the distance between two clusters (aka linkage methods):
- Single linkage: the distance between two clusters is defined as the minimum value of all pairwise distances between the elements of the first cluster and elements of the second cluster.
- Complete linkage: the distance between two clusters is defined as the maximum value of all pairwise distances between the elements of the first cluster and elements of the second cluster.
- Average linkage: the distance between two clusters is defined as the average distance between the elements of the first cluster and elements of the second cluster.
- Centroid linkage: the distance between two clusters is defined as the distance between the centroids of the two clusters.
Q43. What is the main disadvantage of K means clustering algorithm?
a) Non-deterministic nature
b) Initialization of centroid
c) Value of K
Answer: b) Initialization of centroid
The main drawback of k-means algorithm is that it is very much dependent on the initialization of the centroids or the mean points.
In this way, if a centroid is introduced to be a "far away" point, it may very well wind up without any data point related with it and simultaneously more than one cluster may wind up connected with a solo centroid. Likewise, more than one centroids may be introduced into a similar group bringing about poor clustering.
Q44. What is the Time Complexity of Mean Shift Clustering Algorithm?
a) O(N)
b) O(N^2)
c) O(N^0.5)
d) O(logN)
Answer: b) O(N^2)
The Mean Shift clustering algorithm can be computationally expensive for large datasets, because we have to iteratively follow our procedure for each data point.
It has a time complexity of O(N^2), where n is the number of data points.
Q45. In Mean Shift Clustering Algorithm, for which value of bandwidth will convergence be missed?
a) Too high
b) Too low
c) 0
Answer: b) Too low
For Mean Shift Clustering Algorithm:
- If the bandwidth is too small, enough data points may be missed, and convergence might never be reached.
- If the bandwidth is too large, a few clusters may be missed completely.
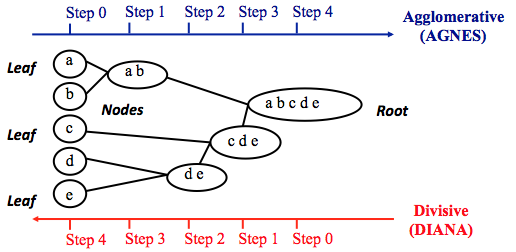
Q46. There are 2 Types of Hierarchical Clustering. Which one is top down approach?
a) Agglomerative method
b) Divisive method
Answer: b) Divisive method
There are two main methods for performing hierarchical clustering:
-
Agglomerative method: it is a bottom-up approach, in the beginning, we treat every data point as a single cluster. Then, we compute similarity between clusters and merge the two most similar clusters. We repeat the last step until we have a single cluster that contains all data points.
-
Divisive method: it is a top-down approach, where we put all data points in a single cluster. Then, we divide this single cluster into two clusters and recursively do the same thing for the two clusters until there is one cluster for every data point. This method is less common than the agglomerative method.
Q47. What is the meaning of homoscedasticity?
a) No outliers
b) Equal variance
c) F-Score = 1
d) Mean within 20%
Answer: b) Equal variance
Homoscedasticity means equal variance.
Q48. Expectation Maximization Clustering is an example of?
a) Hard clustering
b) Soft Clustering
Answer: b) Soft Clustering
Hard clustering means we have non-overlapping clusters, where each instance belongs to one and only one cluster. In a soft clustering method, a single individual can belong to multiple clusters, often with a confidence (belief) associated with each cluster.
Expectation Maximization Clustering is a Soft Clustering method. This means, that it will not form fixed, non-intersecting clusters. There is no rule for one point to belong to one cluster, and one cluster only. In EM Clustering, we talk about probability of each data point to be present in either of the clusters. It is completely possible for multiple clusters to partly share a portion of the data point, since we are only talking about respective probabilities of the point with respect to the clusters.
Q49. For which distribution, one should not use Normalization?
a) Normal Distribution
b) Gaussian Distribution
c) Exponential Distribution
Answer: b) Gaussian Distribution
Normalization is a good technique to use when you do not know the distribution of your data or when you know the distribution is not Gaussian (a bell curve). Normalization is useful when your data has varying scales and the algorithm you are using does not make assumptions about the distribution of your data, such as k-nearest neighbors and artificial neural networks.
Q50. What is the assumption of Standardization?
a) Data is uniformly distributed
b) Data is random
c) Data has Gaussian distribution
Answer: c) Data has Gaussian distribution
Standardization assumes that your data has a Gaussian (bell curve) distribution. This does not strictly have to be true, but the technique is more effective if your attribute distribution is Gaussian. Standardization is useful when your data has varying scales and the algorithm you are using does make assumptions about your data having a Gaussian distribution, such as linear regression, logistic regression, and linear discriminant analysis.
Q51. Which Naive Bayes Classifier has features in binary form?
a) Multinomial Naive Bayes
b) Bernoulli Naive Bayes
c) Gaussian Naive Bayes
Answer: b) Bernoulli Naive Bayes
Bernoulli Naive Bayes is used for discrete data and it works on Bernoulli distribution. The main feature of Bernoulli Naive Bayes is that it accepts features only as binary values like true or false, yes or no, success or failure, 0 or 1 and so on. So when the feature values are binary we know that we have to use Bernoulli Naive Bayes classifier.
Q52. In a Random Decision Forest, what is the n_estimators hyper-parameter?
a) Number of decision trees
b) Degree of randomness
c) Number of features
Answer: a) Number of decision trees
Important Hyperparameters of Random Decision Forest:
- n_estimators: This indicates the number of decision trees we intend to use. Generally, the higher the number of trees, the more accurate will our model be.
- random_state: Since Random Forest uses a considerable degree of randomness in it's approach, our predictions may vary with different random states. We use this for consistency.
- max_features: This helps in increasing the accuracy of our model. It is the maximum number of features to consider when splitting a node.
Q53. Which one of the following is not an ensemble method?
a) Bagging
b) Boosting
c) Stacking
d) None
Answer: d) None
Different Ensemble techniques used in the domain of Machine Learning:
- Bagging
- Boosting
- Stacking
Q54. What is the full form of Bagging ensemble technique?
a) Bayesian-aging
b) Bootstrap Aggregation
c) Bag of Bags
d) None
Answer: b) Bootstrap Aggregation
Bagging, also known as Bootstrap Aggregation is an ensemble technique in which the main idea is to combine the results of multiple models (for instance- say decision trees) to get generalized and better predictions. The critical concept in Bagging technique is Bootstrapping, which is a sampling technique(with replacement) in which we create multiple subsets (also known as bags) of observations using the original data.
Q55. Which ensemble technique uses the concept of weak learners?
a) Bagging
b) Boosting
c) Stacking
Answer: b) Boosting
Boosting is a type of ensemble technique which combines a set of weak learners to form a strong learner. As we saw above, Bagging is based on parallel execution of base learners while on the other hand Boosting is a sequential process, wherein each subsequent model attempts to rectify the errors made by the previous model in the sequence which indicates succeeding models are dependent on the previous model.
The terminology 'weak learner' refers to a model which is slightly better than the random guessing model but nowhere close to a good predictive model. In each iteration, a larger weight is assigned to the points which were misclassified in the previous iteration, such that, they are now predicted correctly. The final output in case of classification is computed using weighted majority vote similarly for regression we use the weighted sum.
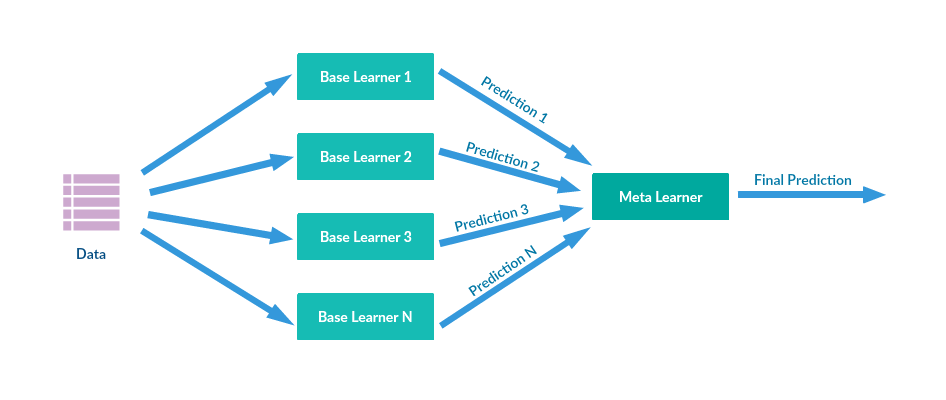
Q56. What is Stacking?
a) Stacked Generalization
b) Modified Bagging
Answer: a) Stacked Generalization
Stacking also referred to Stacked Generalization is an ensemble technique which combines predictions from multiple models to create a new model. The new model is termed as meta-learner. In general, Stacking usually provides a better performance compared to any of the single model. The following figure illustrates the Stacking technique:
With this article at OpenGenus, you must have a solid practice of Machine Learning Interview questions. If you got any question wrong, dive deeper into the topic and get well prepared for Machine Learning Interview.