
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes
In this post, we covered the introduction to Regularization. In this post, we will go over some of the regularization techniques widely used and the key difference between those.

In order to create less complex model when you have a large number of features in your dataset, some of the Regularization techniques used to address over-fitting and feature selection are:
- L1 Regularization
- L2 Regularization
A regression model that uses L1 regularization technique is called Lasso Regression and model which uses L2 is called Ridge Regression.
The key difference between these two is the penalty term.
L1 regularization / Lasso Regression
Lasso Regression (Least Absolute Shrinkage and Selection Operator) adds “absolute value of magnitude” of coefficient as penalty term to the loss function.
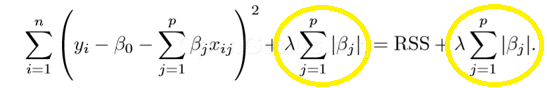
Again, if lambda is zero then we will get back OLS whereas very large value will make coefficients zero hence it will under-fit.
L2 regularization / Ridge Regression
Ridge regression adds “squared magnitude” of coefficient as penalty term to the loss function. Here the highlighted part represents L2 regularization element.
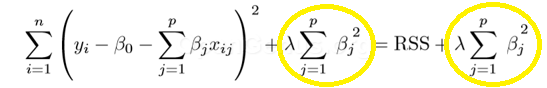
Here, if lambda is zero then you can imagine we get back OLS. However, if lambda is very large then it will add too much weight and it will lead to under-fitting. Having said that it’s important how lambda is chosen. This technique works very well to avoid over-fitting issue.
Difference between L1 and L2 regularization
The key difference between these techniques is that Lasso shrinks the less important feature’s coefficient to zero thus, removing some feature altogether. So, this works well for feature selection in case we have a huge number of features.
Traditional methods like cross-validation, stepwise regression to handle overfitting and perform feature selection work well with a small set of features but these techniques are a great alternative when we are dealing with a large set of features.

