Regularization

Reading time: 25 minutes

One of the most important thing to take care of while doing a machine learning project is to prevent overfitting.Overfitting is a problem when your model that you trained depends too much on your training set which results in a high accuracy on your training set and a very low accuracy on your test dataset.This happens because your model is trying too hard to capture the noise in your training dataset.

Bias-Variance Dilemma

We say that a model is biased when it has no capacity to learn anything.In other words,whatever way you train the model or with whatever data you train,the model will react in the sameway.In this case we can say that the data is underfit.

Variance occurs when your model is extremely perceptive to the training data and can only replicate the stuff that it has seen before.The problem with this is that it will react poorly in situations it hasn’t seen before and because it doesn’t have the right bias to generalize to new stuff.In this case we say that the data is overfit.

Practically we want our model to be somewhere in the middle of these two,called the bias-variance trade-off.You need your model to perform well both on situations it has seen before as well as to new situations.

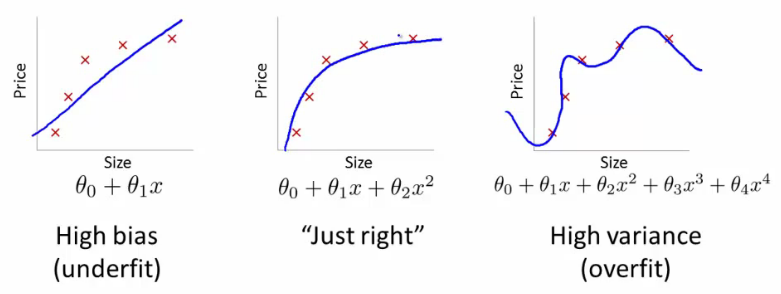
Regularization is a methode used to reduce the variance of your model and increase the bias.It is used when your model overfits the training data.

For eg:
Suppose your model gives an accuracy of 98% on your training set and only gives about 70% on your test set.This is a case of high variance.

Regularization is a method of regression that shrinks the coefficients of your models so that your model won’t be able to do complex learnings which helps to reduce the risk of overfitting.

We will take the example of a simple linear regression,

$$ Y ≈ β0 + β1X1 + β2X2 + … + βpXp $$

The loss function for this regression would be,

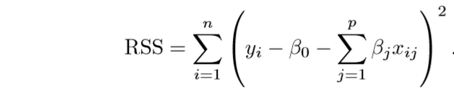
RSS is the residual sum of squares.

Here β0, β1... βp are the coefficients.This will adjust the coefficients based on your training data. If there is noise in the training data, then the estimated coefficients won’t generalize well to the future data.In a way,when the value of you coefficients is high,your model will be more inclined to the training data set which inturn overfits your model.This is where regularization actually comes in and regularizes(shrinks) these learned estimates.

The way you achieve this is that you penalize your model for higher values of coefficients.One way of doing this is by using this cost function

$$J = RSS + λ(Σ (βk ^ 2 )) where,k=0,1,2...p $$

λ is a parameter that defines how much bias our model should posses.A higher value would mean that our model has higher bias.Choosing a value for λ is thus important.

There are other cost functions that achieve regularization,which you can check if you are intersted.This is one of the most common ones used and is called Ridge Regression.

Another method to do regularization is called Lasso regression. Lasso Regression differs from ridge regression only in penalizing the high coefficients.

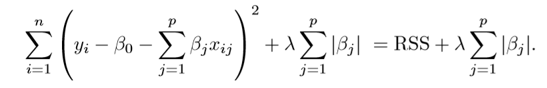
Read more about this if you are interested.

Why does this work?

A higher value of coefficients implies that a point in the training set is given a lot of importance while the model learns.So,even for the noisy values,this importance is given which is bad for generelization.So,regularizing the value of these coefficients helps us reduce the importance given to point in the training set which inturn helps in reducing overfitting.

Regularization is heavily used in neural networks to reduce overfitting.In neural networks,it actually helps in reducing overfitting without changing the structure of neural network.(Read about L1 and L2 regularization methods if you are intersted.)