
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
Decision Tree is a popular machine learning algorithm mainly used for classification.

The main idea of a decision tree is to split our data set into many smaller and smaller datasets in many steps based on features until you reach a node which is small enough to contain datapoints that falls under the same label.
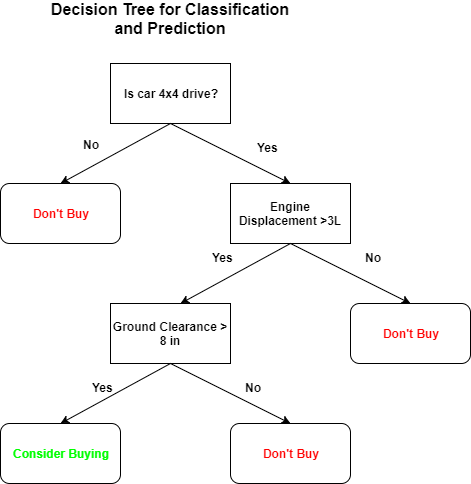
This is a good example of a decision tree algorithm.
At each step we are narrowing down our data sets by asking a question at each step and by responding accordingly.
Now we have a basic understanding of decision trees.The next thing is how to construct them or how to find the questions to be asked?
For this we use something called “entropy” and “information gain”.
Entropy
We define entropy as,
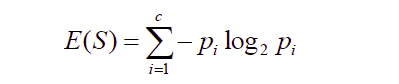
here “$p_i$" is the probability that the element ‘i’ occurs in your feature ‘S’
For eg,
If “speedlimit” and “Traffic” are your features with “Slow” and “Fast” being labels,

$P_slow$=3/4 ; $P_fast$=1/4.
Using this entropy can be calculated.
Information Gain
Now information gain is,
Information gain = entropy(parent) - [weighted average]entropy(children)
Note that entropy(parent) of the root node is always taken to be one.
Now the all possible splits are made for each feature and information gain is calculated.The main goal is to maximize information gain at each step.So,the split for the feature that gives maximum information gain is taken for splitting the data into simpler datasets.
For eg,
suppose we split based on speed limit which has 2 categories,”Yes” or “No”.
“Yes” contains 2 “Slow” and 1 ”Fast” points.Now we find Pslow and Pfast for “Yes” and calculate entropy.We will do the same for “No”.
Now we calculate the information gain using these values.We do the same for Traffic and find the information gain.Which ever gives us the larger information gain,We make a split using that.
This can be done either till there is a predefined number of datapoints in the subset or till the subests contains only one label of datapoints
Note:
Decision tree is a good algorithm for doing non-linear classification and can be used for regression as well.
Make sure that your model doesn’t overfit towards the training data. There is also another method for splitting by using gini cost function.
Example
Now we will look in to an example
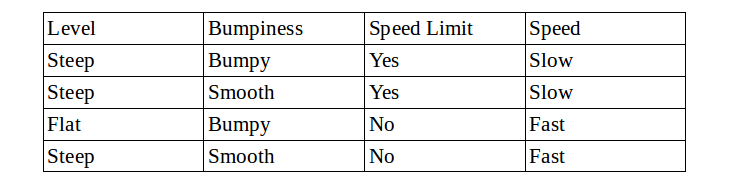
Consider this dataset as your training set.(“Level”,”Bumpiness” and “Speed Limit” of a road are features and “Speed” is the label.
We will built a descision tree.
We will start with the feature “Level”.
There will be 2 branches,”Steep” and “Flat”.
“Steep” consists of :
- 2 “Slow” nodes
- 1 “Fast” node
“Flat” consists of :
- 1 ”Fast” node.
Now for “Flat” node
$P_{fast}$ = 1 , $P_{slow}$ = 0
$E(Flat) = (P_{fast} * log(P_{fast}) + P_{slow} * log(P_{slow})) * (-1)$
$E(Flat) = 1 * log(1) + 0 * log(0) = 0$
Similarly for “Steep” node
$P_{fast}$ = 1/3 , $P_{slow}$ = 2/3
$E(steep) = (P_{fast} * log(P_{fast}) + P_{slow} * log(P_{slow})) * (-1)$
$E(steep) = (1/3) * log(1/3) + (2/3) * log(2/3)$
$E(steep) = 0.9184$
Now since we have entropy, we can calculate information gain.
$[Weighted Average] entropy(children) = (3/4) * 0.9184 + (1/4) * 0 = 0.73605$
$ Information gain = 1 - 0.73605 = 0.3112$
So this is the information gain if we decide to split on the basis of “Level”.
Now, we will find the information gain if we split on the basis of bumpiness.
Doing the same steps as before,
$Entropy(bumpy) = ((1/2) * log(1/2) + (1/2) * log(1/2)) * (-1) = 1.0$
$Entropy(Smooth) = ((1/2) * log(1/2) + (1/2) * log(1/2)) * (-1) = 1.0$
$Information gain = 1 - ((1/2) * 1 + (1/2) * 1) = 1 - 1 = 0$
Now,try calculating the same for speed limit.
For “Speed limit”,the information gain turns out to be 1.0.
So, now we Calculated for all the features and information gain turns out to be maximum if we make the split on “Speed Limit”.
So we make the split for the first node of the decision tree based on speed limit.Now the entropy that you got for “Speed Limit” becomes the entropy (parent) for the immediate children nodes.
We can continue doing this for the children nodes until there is a predefined number of datapoints in the subset or till the subests contains only one label of datapoints.
When does it terminate?
The algorithm terminates for the following conditions:
- Either it has divided into classes that are pure (only containing members of single class )
- Some criteria of classifier attributes are met.

