
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 9 minutes
A red–black tree is a kind of self-balancing binary search tree in computer science. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.
We will explore the deletion operation on a Red Black tree in the session. Deleting a value in Red Black tree takes O(log N) time complexity and O(N) space complexity.
- In addition to the requirements imposed on a binary search tree the following must be satisfied by a red–black tree:
- Each node is either red or black.
- The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
- All leaves (NIL) are black.
- If a node is red, then both its children are black.
- Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes.
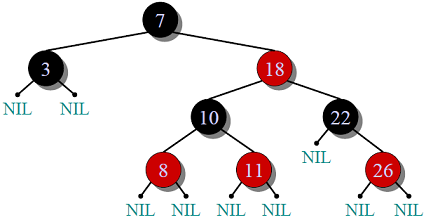
The figure depicts the basic structure of Red Black Tree.
Algorithm
- Basic operations associated with Red Black Tree:
-
Deletion of a node in Red Black Tree:
1) Perform standard Binary Search Tree delete. When we perform standard delete operation in BST, we always end up deleting a node which is either leaf or has only one child (For an internal node, we copy the successor and then recursively call delete for successor, successor is always a leaf node or a node with one child). So we only need to handle cases where a node is leaf or has one child. Let v be the node to be deleted and u be the child that replaces v (Note that u is NULL when v is a leaf and color of NULL is considered as Black).
2) Simple Case: If either u or v is red, we mark the replaced child as black (No change in black height). Note that both u and v cannot be red as v is parent of u and two consecutive reds are not allowed in red-black tree.
3) If Both u and v are Black.
3.1) Color u as double black. Now our task reduces to convert this double black to single black. Note that If v is leaf, then u is NULL and color of NULL is considered as black. So the deletion of a black leaf also causes a double black.
3.2) Do following while the current node u is double black and it is not root. Let sibling of node be s.
(a): If sibling s is black and at least one of sibling’s children is red, perform rotation(s). Let the red child of s be r. This case can be divided in four subcases depending upon positions of s and r.(i) Left Left Case (s is left child of its parent and r is left child of s or both children of s are red). This is mirror of right right case shown in below diagram.
(ii) Left Right Case (s is left child of its parent and r is right child). This is mirror of right left case shown in below diagram.
(iii) Right Right Case (s is right child of its parent and r is right child of s or both children of s are red)
(iv) Right Left Case (s is right child of its parent and r is left child of s)
(b): If sibling is black and its both children are black, perform recoloring, and recur for the parent if parent is black.
(c): If sibling is red, perform a rotation to move old sibling up, recolor the old sibling and parent. The new sibling is always black (See the below diagram). This mainly converts the tree to black sibling case (by rotation) and leads to case (a) or (b). This case can be divided in two subcases.
(i) Left Case (s is left child of its parent). This is mirror of right right case shown in below diagram. We right rotate the parent p.
(ii) Right Case (s is right child of its parent). We left rotate the parent p.3.3) If u is root, make it single black and return (Black height of complete tree reduces by 1).
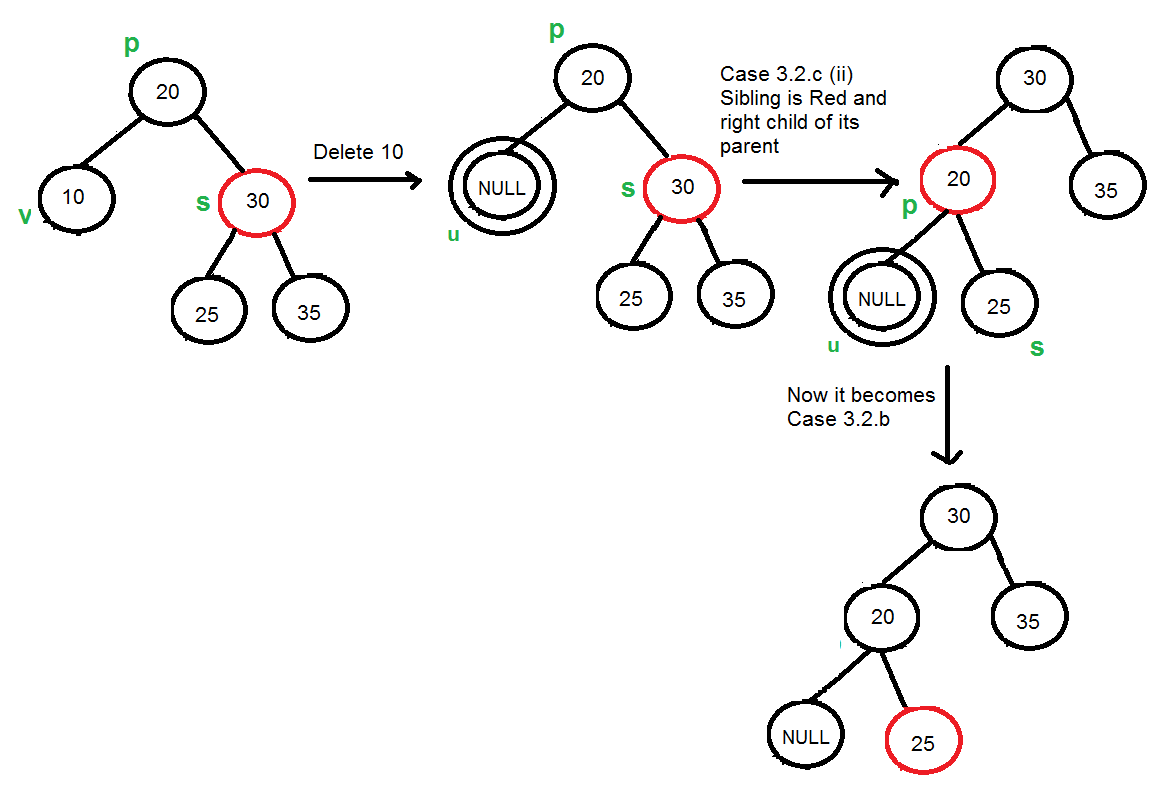
The figure illustrates the deletion of an element from a Red Black Tree.
Complexity
-
Average and Worst case deletion time complexity:
Θ(log n) -
Average and Worst case Space complexity:
Θ(n)
Pseudocode
Deletion
RB-DELETE(T, z)
if z->left = null or z->right = null
then y ← z
else y ← TREE-SUCCESSOR(z)
if y->left ≠ null
then x ← y->left
else x ← y->right
x->p ← y->p
if y->p = null
then T->root ← x
else if y = y->p->left
then y->p->left ← x
else y->p->right ← x
if y 3≠ z
then z->key ← y->key
copy y's satellite data into z
if y->color = BLACK
then RB-DELETE-FIXUP(T, x)
return y
RB-DELETE-FIXUP(T, x)
while x ≠ T->root and x->color = BLACK
do if x = x->p->left
then w ← x->p->right
if w->color = RED
then w->color ← BLACK Case 1
x->p->color ← RED Case 1
LEFT-ROTATE(T, x->p) Case 1
w ← x->p->right Case 1
if w->left->color = BLACK and w->right->color = BLACK
then w->color ← RED Case 2
x ← x->p Case 2
else if w->right->color = BLACK
then w->left->color ← BLACK Case 3
w->color ← RED Case 3
RIGHT-ROTATE(T, w) Case 3
w ← x->p->right Case 3
w->color ← x->p->color Case 4
x->p->color ← BLACK Case 4
w->right->color ← BLACK Case 4
LEFT-ROTATE(T, x->p) Case 4
x ← T->root Case 4
else (same as then clause with "right" and "left" exchanged)
x->color ← BLACK
Implementations
Implementations of Red Black Tree is as follows:
- C++
C++
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cassert>
#define INDENT_STEP 4
using namespace std;
enum color { RED, BLACK };
/*
* Node RBTree Declaration
*/
typedef struct rbtree_node
{
enum color color;
void *key;
void *value;
rbtree_node *left, *right, *parent;
}*node;
typedef struct rbtree_t
{
node root;
}*rbtree;
/*
* Class RBTree Declaration
*/
class RBTree
{
public:
typedef int (*compare_func)(void* left, void* right);
rbtree rbtree_create();
void* rbtree_lookup(rbtree t, void* , compare_func compare);
void rbtree_insert(rbtree t, void* , void* , compare_func compare);
void rbtree_delete(rbtree t, void* , compare_func compare);
node grandparent(node n);
node sibling(node n);
node uncle(node n);
void verify_properties(rbtree t);
void verify_property_1(node root);
void verify_property_2(node root);
color node_color(node n);
void verify_property_4(node root);
void verify_property_5(node root);
void verify_property_5_helper(node n, int , int*);
node new_node(void* key, void* , color , node , node);
node lookup_node(rbtree t, void* , compare_func compare);
void rotate_left(rbtree t, node n);
void rotate_right(rbtree t, node n);
void replace_node(rbtree t, node oldn, node newn);
void insert_case1(rbtree t, node n);
void insert_case2(rbtree t, node n);
void insert_case3(rbtree t, node n);
void insert_case4(rbtree t, node n);
void insert_case5(rbtree t, node n);
node maximum_node(node root);
void delete_case1(rbtree t, node n);
void delete_case2(rbtree t, node n);
void delete_case3(rbtree t, node n);
void delete_case4(rbtree t, node n);
void delete_case5(rbtree t, node n);
void delete_case6(rbtree t, node n);
};
/*
* Return Grandparent of Node
*/
node RBTree::grandparent(node n)
{
assert (n != NULL);
assert (n->parent != NULL);
assert (n->parent->parent != NULL);
return n->parent->parent;
}
/*
* Return Sibling of Node
*/
node RBTree::sibling(node n)
{
assert (n != NULL);
assert (n->parent != NULL);
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
/*
* Return Uncle of Node
*/
node RBTree::uncle(node n)
{
assert (n != NULL);
assert (n->parent != NULL);
assert (n->parent->parent != NULL);
return sibling(n->parent);
}
/*
* Verifying Properties of Red black Tree
*/
void RBTree::verify_properties(rbtree t)
{
verify_property_1 (t->root);
verify_property_2 (t->root);
verify_property_4 (t->root);
verify_property_5 (t->root);
}
/*
* Verifying Property 1
*/
void RBTree::verify_property_1(node n)
{
assert (node_color(n) == RED || node_color(n) == BLACK);
if (n == NULL)
return;
verify_property_1(n->left);
verify_property_1(n->right);
}
/*
* Verifying Property 2
*/
void RBTree::verify_property_2(node root)
{
assert (node_color(root) == BLACK);
}
/*
* Returns color of a node
*/
color RBTree::node_color(node n)
{
return n == NULL ? BLACK : n->color;
}
/*
* Verifying Property 4
*/
void RBTree::verify_property_4(node n)
{
if (node_color(n) == RED)
{
assert (node_color(n->left) == BLACK);
assert (node_color(n->right) == BLACK);
assert (node_color(n->parent) == BLACK);
}
if (n == NULL)
return;
verify_property_4(n->left);
verify_property_4(n->right);
}
/*
* Verifying Property 5
*/
void RBTree::verify_property_5(node root)
{
int black_count_path = -1;
verify_property_5_helper(root, 0, &black_count_path);
}
void RBTree::verify_property_5_helper(node n, int black_count, int* path_black_count)
{
if (node_color(n) == BLACK)
{
black_count++;
}
if (n == NULL)
{
if (*path_black_count == -1)
{
*path_black_count = black_count;
}
else
{
assert (black_count == *path_black_count);
}
return;
}
verify_property_5_helper(n->left, black_count, path_black_count);
verify_property_5_helper(n->right, black_count, path_black_count);
}
/*
* Create Red Black Tree
*/
rbtree RBTree::rbtree_create()
{
rbtree t = new rbtree_t;
t->root = NULL;
verify_properties(t);
return t;
}
/*
* Creating New Node of Reb Black Tree
*/
node RBTree::new_node(void* k, void* v, color n_color, node left, node right)
{
node result = new rbtree_node;
result->key = k;
result->value = v;
result->color = n_color;
result->left = left;
result->right = right;
if (left != NULL)
left->parent = result;
if (right != NULL)
right->parent = result;
result->parent = NULL;
return result;
}
/*
* Look Up through Node
*/
node RBTree::lookup_node(rbtree t, void* key, compare_func compare)
{
node n = t->root;
while (n != NULL)
{
int comp_result = compare(key, n->key);
if (comp_result == 0)
{
return n;
}
else if (comp_result < 0)
{
n = n->left;
}
else
{
assert(comp_result > 0);
n = n->right;
}
}
return n;
}
/*
* RbTree Look Up
*/
void* RBTree::rbtree_lookup(rbtree t, void* key, compare_func compare)
{
node n = lookup_node(t, key, compare);
return n == NULL ? NULL : n->value;
}
/*
* Rotate left
*/
void RBTree::rotate_left(rbtree t, node n)
{
node r = n->right;
replace_node(t, n, r);
n->right = r->left;
if (r->left != NULL)
{
r->left->parent = n;
}
r->left = n;
n->parent = r;
}
/*
* Rotate right
*/
void RBTree::rotate_right(rbtree t, node n)
{
node L = n->left;
replace_node(t, n, L);
n->left = L->right;
if (L->right != NULL)
{
L->right->parent = n;
}
L->right = n;
n->parent = L;
}
/*
* Replace a node
*/
void RBTree::replace_node(rbtree t, node oldn, node newn)
{
if (oldn->parent == NULL)
{
t->root = newn;
}
else
{
if (oldn == oldn->parent->left)
oldn->parent->left = newn;
else
oldn->parent->right = newn;
}
if (newn != NULL)
{
newn->parent = oldn->parent;
}
}
/*
* Insert node into RBTree
*/
void RBTree::rbtree_insert(rbtree t, void* key, void* value, compare_func compare)
{
node inserted_node = new_node(key, value, RED, NULL, NULL);
if (t->root == NULL)
{
t->root = inserted_node;
}
else
{
node n = t->root;
while (1)
{
int comp_result = compare(key, n->key);
if (comp_result == 0)
{
n->value = value;
return;
}
else if (comp_result < 0)
{
if (n->left == NULL)
{
n->left = inserted_node;
break;
}
else
{
n = n->left;
}
}
else
{
assert (comp_result > 0);
if (n->right == NULL)
{
n->right = inserted_node;
break;
}
else
{
n = n->right;
}
}
}
inserted_node->parent = n;
}
insert_case1(t, inserted_node);
verify_properties(t);
}
/*
* Inserting Case 1
*/
void RBTree::insert_case1(rbtree t, node n)
{
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(t, n);
}
/*
* Inserting Case 2
*/
void RBTree::insert_case2(rbtree t, node n)
{
if (node_color(n->parent) == BLACK)
return;
else
insert_case3(t, n);
}
/*
* Inserting Case 3
*/
void RBTree::insert_case3(rbtree t, node n)
{
if (node_color(uncle(n)) == RED)
{
n->parent->color = BLACK;
uncle(n)->color = BLACK;
grandparent(n)->color = RED;
insert_case1(t, grandparent(n));
}
else
{
insert_case4(t, n);
}
}
/*
* Inserting Case 4
*/
void RBTree::insert_case4(rbtree t, node n)
{
if (n == n->parent->right && n->parent == grandparent(n)->left)
{
rotate_left(t, n->parent);
n = n->left;
}
else if (n == n->parent->left && n->parent == grandparent(n)->right)
{
rotate_right(t, n->parent);
n = n->right;
}
insert_case5(t, n);
}
/*
* Inserting Case 5
*/
void RBTree::insert_case5(rbtree t, node n)
{
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left)
{
rotate_right(t, grandparent(n));
}
else
{
assert (n == n->parent->right && n->parent == grandparent(n)->right);
rotate_left(t, grandparent(n));
}
}
/*
* Returns Maximum node
*/
node RBTree::maximum_node(node n)
{
assert (n != NULL);
while (n->right != NULL)
{
n = n->right;
}
return n;
}
/*
* Compare two nodes
*/
int compare_int(void* leftp, void* rightp)
{
int left = (int)leftp;
int right = (int)rightp;
if (left < right)
return -1;
else if (left > right)
return 1;
else
{
assert (left == right);
return 0;
}
}
/*
* Print RBTRee
*/
void print_tree_helper(node n, int indent)
{
int i;
if (n == NULL)
{
fputs("<empty tree>", stdout);
return;
}
if (n->right != NULL)
{
print_tree_helper(n->right, indent + INDENT_STEP);
}
for(i = 0; i < indent; i++)
fputs(" ", stdout);
if (n->color == BLACK)
cout<<(int)n->key<<endl;
else
cout<<"<"<<(int)n->key<<">"<<endl;
if (n->left != NULL)
{
print_tree_helper(n->left, indent + INDENT_STEP);
}
}
void print_tree(rbtree t)
{
print_tree_helper(t->root, 0);
puts("");
}
/*
* Main Contains Menu
*/
int main()
{
int i;
RBTree rbt;
rbtree t = rbt.rbtree_create();
for (i = 0; i < 12; i++)
{
int x = rand() % 10;
int y = rand() % 10;
print_tree(t);
cout<<"Inserting "<<x<<" -> "<<y<<endl<<endl;
rbt.rbtree_insert(t, (void*)x, (void*)y, compare_int);
assert(rbt.rbtree_lookup(t, (void*)x, compare_int) == (void*)y);
}
return 0;
}
Applications
Importance of Red Black Tree:
- Completely Fair Scheduler in Linux Kernel
- Computational Geometry Data structures
- In various implementations of Associative Data structures (for e.g C++ STL uses RB tree internally to implement Set and Map)
