In this article, we have listed and explained the real-life applications of 24 Different Data Structures ranging from common ones like Array, Linked List to Geometric Data Structures like R-Tree to Probabilistic Data Structures like LogLog.

Data structures

Table of contents

• Data Structures
• Arrays
• Matrix
• Vectors
• Strings
• Linked List
• Stack
• Queue
• Binary Tree
• Binary Search Tree
• Heap
• Hashing
• Graph
• Suffix Array
• Trie
• X/Y-Trie
• Suffix Tree
• Bloom Filter
• B-Tree
• Segment Tree
• n-ary Tree
• K-Dimensional Tree
• R-Tree
• Count Min Sketch
• LogLog

Data Structures

The field of computer science started emerging in the mid-20th century. As it started to grow the need to organize and store data, in a way that made it easier to access and manipulate also emerged. Then the scientists began to adapt the mathematical concepts of data organization to meet the needs of the computers, which gave birth to the field of Data Structures.

In the early days the data structures developed were relatively simple and included things like arrays and linked lists, but over
time as the computers became more powerful, new algorithms and techniques were developed, the field of data structures grew to
encompass a wide variety of more complex data structures such as trees, graphs and other advanced structures.

The study of data structures and algorithms is considered as a fundamental part of computer science, and it continues to evolve day by day. As our computer technology advances, new methods are developed and new areas of applications are emerging. Today data structure and algorithms are important aspects in computer science and are used in almost all areas of computer science including operating systems, databases, compilers, artificial intelligence, and more.

Data structures are classified into linear data structure and non-linear data structure.

• Linear data structure: In these data structures the data is arranged linearly. Its further divided into:
  • Static data structure: Those linear data structure which has fixed size. eg: Array
  • Dynamic data structure: Those linear data structures which does not have a fixed size. It can be randomly updated during the runtime. eg: Vectors;
• Non-linear data structure: In these data structures the data will not be placed linearly. eg: Trees, Graphs etc

Now lets get to know about some data structures.

Arrays

Earlier, programmers had to use multiple variables to store related data, which make the code more difficult to write, read and maintain. This also made it more difficult to perform mathematical operations on data such as sorting or searching.

Arrays was introduced in 1945 to solve these problems by allowing the programmers to store multiple values under a single variable name, and it provided the indexing system which made it easy to access and manipulate individual elements of the array. They also provided a way to improve the performance of the program in terms of memory usage.

So, arrays are data structures that stores a collection of elements of any data type in a continuous memory space.

Some basic operations which we can do in an array are: accessing an element, traversing the array, searching an element, insertion of an element deletion of an element, sorting, reversing the array etc.

Real world applications of arrays:

• Database indexing: Arrays are used to index the data in a database, which makes its retrieval fast and efficient.
• Image processing: Arrays are used to represent an image where each element of the array represents the color of the pixel. Image processing algorithms such as filtering, resizing and compression can be implemented using arrays.
• Game Programming: Arrays are used to store data such as the positions of objects in a game world, scores of characters etc.
• Sorting and searching: Arrays are used to store data that needs to be sorted or searched.
• Spreadsheets: Spreadsheets software such as Microsoft Excel, Google Sheets use arrays to store data and perform calculations on it.

Matrix

The need for matrices arose from the requirement to efficiently store and manipulate large collections of data that have a two-dimensional structure.

For example, a matrix can be used to represent a table of numbers, where each row represents a different record and each column represents a different field.

Matrix is a two dimensional array of elements, usually numbers or expressions. Each cell of a matrix is denoted by its row and column indices, and each of these cells are accessed using this notation matrix[row][column]. Matrices are also known as a two-dimensional arrays, tables or grids.

The different operations carried out in a matrix are: matrix addition, subtraction, scalar multiplication, matrix multiplication, transpose, determinant; inverse, trace, eigenvalues and eigenvectors.

Real world applications of matrix:

• Linear Algebra: Matrices are used to represent and manipulate systems of linear equations, which are used in a variety of fields in science like engineering, physics, computer graphics etc.
• Computer Graphics: Matrices are used to represent and manipulate geometric transformations such as translation, rotation, scaling etc.
• Machine Learning: It is used to represent and manipulate data in machine learning algorithms like neural networks, Principal Component Analysis (PCA) etc.
• Robotics: Matrices are used to represent and manipulate the movements of robotic systems, such as in kinematics and dynamics of robots.
• Cryptography: Matrices are used to represent and manipulate data in encryption and decryption algorithms, such as in the Hill cipher and the RSA algorithm.

Vectors

Arrays are powerful data structure that can be used to store and manipulate large sets of data, but it still have some limitations when it comes to certain things.

One main limitation is that they do not have any built-in mathematical operations defined for them. This makes it more difficult to perform mathematical operations on arrays. Another limitation is that they do not have a clear geometric interpretation. They do not have any built-in concepts such as length, angle or direction, which are important for representing geometric objects. Also a vectors size is not fixed whereas an arrays size is.

Hence vectors! A vector is a one-dimensional array of elements, usually numbers, symbols or expressions. Vectors are similar to arrays in that they store a collection of elements. Vectors are specifically designed to represent mathematical objects that have mathematical operations defined for them, such as addition, subtraction, and scalar multiplication. This makes it much simpler to perform mathematical operations on vectors.

On top of that vectors have a clear geometric interpretation as they have a direction and a magnitude. This makes it easy to reason about the properties of the vectors in space, such as the distance between two vectors, or the angle between two vectors etc.

Some common operations in a vector are: Vector addition and subtraction, scalar multiplication, dot product, cross product, magnitude, projection etc.

Some real-world applications are:

• Physics: Vectors are used to represent and manipulate physical quantities like position, velocity etc.
• Computer graphics: Its used to represent and manipulate geometric transformations such as translation, rotation and scaling.
• Control Systems: It is used to represent and manipulate systems of linear equations in control systems, such as in the design of controllers for dynamic systems.
• Navigation: Vectors are used to represent and manipulate geographic data, such as positions, directions and distances, in navigation and geography applications. Example: Google Maps.
• Economics: Vectors are used to represent and manipulate data in econometrics and other economic fields like in the study of input-output models.

Strings

The need for strings arose from the requirement to efficiently represent and manipulate text data in computer programs. With the development of computer and the rise of the internet, the need for storing and manipulating text data has become increasingly important. With the use of text, human-computer interaction became more natural, which made it easier to use computers for a wide range of tasks, from writing and editing documents, to sending and receiving emails, to searching the web. Strings provide a way to store and manipulate text data in a concise and efficient way. A string is a sequence of characters, such as letters, numbers, symbols, or spaces, that can be stored and manipulated as a single entity.

Some operations in strings are: concatenation, scanning, comparison, slicing, encoding/decoding, sub-stringing, translation and verification.

Some real-world applications are:

• Text processing: They are used to process text data, such as in text editors, word processors, search engines etc.
• Web development: Strings are used to represent and manipulate text data in web development, like in HTML, XML and JSON documents.
• Database management: Strings are used to represent and manipulate text data in databases, such as in SQL queries and database fields.
• Natural Language Processing: Strings are used to represent and manipulate text data in natural language processing, such as in text-to-speech and speech-to-text systems.
• Encryption and Cryptography: Strings are used to represent and manipulate text data in encryption and decryption algorithms, such as in the RSA and AES algorithms.

Linked List

Arrays, which are a common data structure for storing and manipulating data, have a fixed size and cannot be easily resized. This makes it difficult to efficiently store and manipulate dynamic sets of data. Hence the need for a way to effectively store and manipulate dynamic sets of data arose.

A linked list is a data structure that consists of a sequence of elements, called nodes, where each node contains a reference (or "link") to the next node in the list. Linked lists are a powerful data structure that can be used to store and manipulate large sets of data.

These linked list are dynamic data structures that can be easily resized as needed. This makes linked lists well-suited for storing and manipulating dynamic sets of data, such as in applications where elements are frequently added or removed from the list, which are difficult in arrays. Some common operations in a linked lists are: Insertion, deletion, traversal, searching, sorting, counting etc.

Some real-world applications are:

• Operating Systems: Linked lists are used to represent and manipulate data structures such as process control blocks, file systems and memory management.
• Computer Networks: It is used to represent and manipulate data structures like routing table and packet buffers.
• Game Development: It is used to represent and manipulate data structures like game objects, assets and physics simulations.
• Compilers: It is also used to represent and manipulate data structures like symbol table and parse trees.
• Music and audio software: It is used to represent and manipulate data structures like play-lists, audio buffers and effects chains.

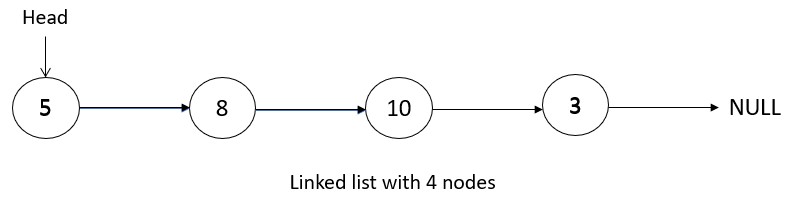
Stack

There was no way to efficiently store and manipulate elements in a specific order, such as a situation where elements need to be added and removed in a specific order, and the most recently added element is the first one to be removed. Hence the need for stacks arose.

A stack is a linear data structure that follows the Last In First Out (LIFO) principle. This means that elements are added and removed from the same end, called the "top" of the stack. When an element is added to the stack, it is said to be "pushed" onto the stack, and when an element is removed from the stack, it is said to be "popped" off of the stack.

Some common operations in a stack are: Push, pop, peek, isEmpty, size etc.

Some real-world applications are:

• Computer Science: Stacks are used to implement algorithms like depth-first search and manage function calls in programming languages.
• Web Browsers: Stacks are used to implement the back and forward buttons in web browsers, allowing users to navigate through a history of web pages.
• Graphical user interface: Stacks are used to implement the undo and redo functionality in text editors, image editors and in every other softwares.
• Calculator and math softwares: Stacks are used to evaluate expressions like arithmetic expressions and expressions in programming languages.
• Computer Networks: It is used to implement routing algorithms and to manage the flow of data packets.

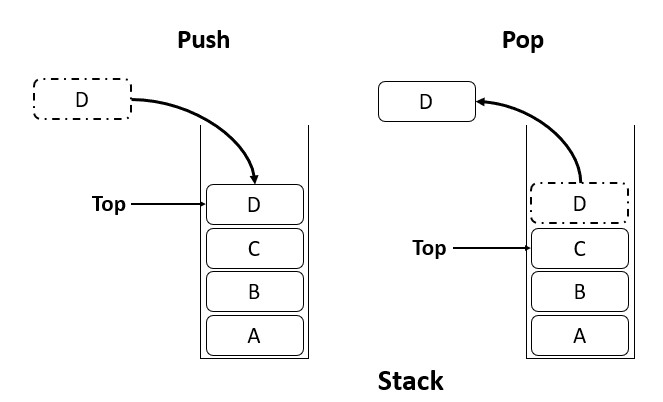
Queue

There came a situation where we needed to store and manipulate data in such a way that the oldest element is the first one to be removed. This was the way how, need for queue data structure arose. A queue is a linear data structure that follows the First In First Out (FIFO) principle, where elements are added to the back of the queue and removed from the front of the queue. The common operations are enqueue, dequeue, peek, isEmpty, size, clear.

Some real-world applications are:

• Operating Systems: Queues are used to manage the process scheduling, where the process are placed in queue based on their priority.
• Computer Networks: Queues are used to manage the flow of packets in a network, such as in buffering incoming data for transmission.
• Simulation: They are used to simulate real-world queues.
• Transportation: Queues are used to manage and optimize the movement of people and goods.
• Gaming: Queues are used to manage game mechanics such as player movements and actions in video games.

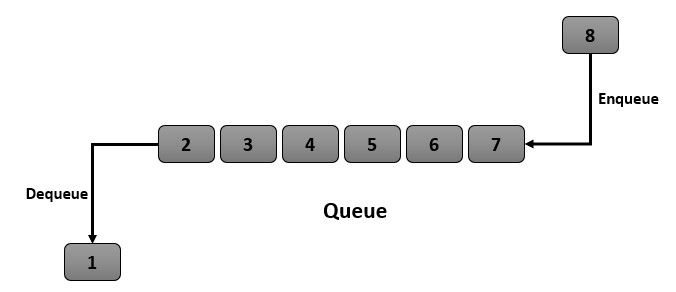
Binary Tree

We needed to efficiently store and manipulate hierarchical data, where each item has a parent-child relationship with other items, for this purpose binary tree was introduced. Its a data structure composed of nodes where each node has at most two child nodes.

Some common operations are: insertion, deletion, searching, traversal etc.

Some real-world applications are:

• File Systems: File systems like NTFS and ext3 use a binary tree to organize and index files.
• Game development: Games like chess, checkers, use a binary tree to represent the game state and perform game-tree search.
• Decision making: Some decision-making algorithm like ID3 algorithm, use binary tree to represent possible decision path and outcomes.
• Data compression: Huffman coding, a lossless data compression technique, uses a binary tree to represent the frequency of characters in a data set.
• Natural Language Processing: Parsing and analyzing of sentence structure, syntactic and semantic analysis, and machine translation, often use binary trees to represent the structure of sentences.

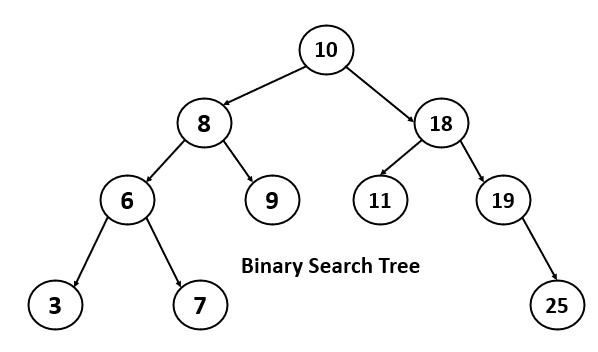
Binary Search Tree

The need for binary search trees arose from the requirement to efficiently store and search for data in a way that allows for fast search times.

A binary search tree (BST) is a type of binary tree that is specifically designed to efficiently store and retrieve data. The main advantage of a BST is its ability to perform fast searches. Because the tree is organized such that all the values in the left subtree of a node are less than its value, and all the values in the right subtree are greater than its value.

Some common operations are: Insertion, deletion, searching, traversal, clone a tree, serialize and de-serialize etc.

Some real world applications are:

• Spell checker: They use BST to quickly find words in a dictionary and check for spelling errors.
• File Systems: Many file systems, such as NTFS and ext3, use a binary search tree to organize and index files.
• Computer Network Routing: Routing algorithms, such as the Spanning Tree Protocol, which finds the shortest path for data to travel through a network, uses binary search trees.
• Expression evaluation: Some compilers and interpreters use BST to store and evaluate mathematical expressions.
• Natural Language Processing: Parsing and analyzing of sentence structure, syntactic and semantic analysis, and machine translation, often use binary search trees to represent the structure of sentences.

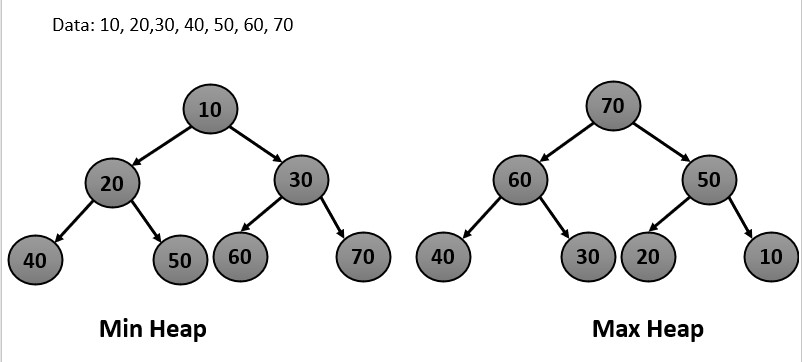
Heap

The need for heap arises from the requirement to efficiently store and retrieve data in a way that allows for fast access to maximum or minimum element. A heap is a specialized tree-based data structure that is used to efficiently implement priority queues. In a max heap value of each node is greater than or equal to the values of its children and vice versa in min heap.

Some common operations are: Accessing min or max element, insertion, deletion, heapifying etc.

Some real-world applications:

• Graph Algorithms: Dijkstra's shortest path algorithm and Prim's minimum spanning tree algorithm use min-heaps to efficiently find the next closest vertex to the current vertex.
• Operating System: operating system uses heaps to manage the memory and schedule processes.
• Priority Queue: Heaps can be used to implement priority queues.
• Huffman coding: Its a lossless data compression technique and it uses a binary heap to build the Huffman tree.
• Medical treatment: In a hospital, patients with the most critical conditions are given priority over patients with less critical conditions. Heaps can be used to implement a priority queues of patients to ensure that the most critical patients are treated first.

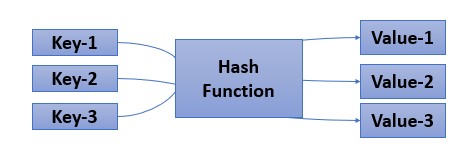
Hashing

We needed a way to efficiently store and retrieve data in a way that allows for fast access to specific elements, and this way hashing was introduced. It is a method of mapping data of any size to a fixed size, called a hash value using a mathematical function called hash function.

Some operations are: insertion, deletion and searching.

Some real-world applications:

• Database indexing: Hashing is used to quickly index and retrieve data from databases.
• Cryptography: Hashing is used in cryptographic algorithms like SHA-256 to create a unique representation of data that can be used for secure communication and data integrity.
• Cache: Hashing is used to quickly identify and retrieve data from a cache.
• Data Compression: Hashing is used to identify and eliminate duplicate data in compression algorithms.
• Network routing: Hashing is used to map IP address to specific network nodes.

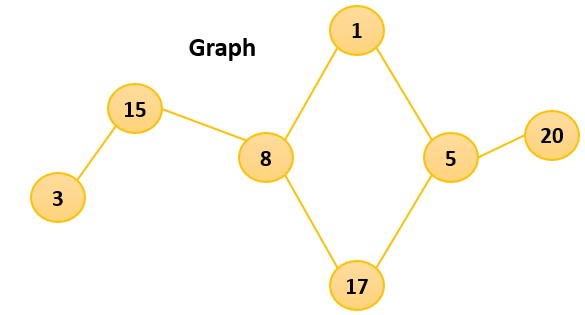
Graph

Graphs came to existence to tackle the problem of representing and modeling relationships between objects or entities. Graphs are a collection of vertices and edges, which connect the vertices. The vertices represent the objects or entities and the edges represent the relationship between them.

Some operations are: Adding and removing a vertex or edge,searching, shortest path, etc.

Some real-world applications are:

• Social Networks: Graphs are used to represent and analyze social networks, such as Facebook, Twitter, Instagram, Youtube etc.
• GPS Navigation: Graphs can be used to represent the road network and to find the shortest path between two locations for GPS navigation systems.
• Web Search: Graphs are used to represent the structure of World Wide Web and to implement web search algorithms.
• Biology: Graphs can be used to represent biological systems, such as proteins interactions or genetic regulatory networks, and to study the relationships between the components.
• Electric Power Grid: Graphs can be used to represent the electric power grid, where nodes represent generators, substations and consumers and edges represent the transmission line.

Suffix Array

The need for suffix arrays arises from the requirement to efficiently search for patterns within a large text. A suffix array is a compact data structure that allows for efficient search for patterns within a large text. It is an array of all the possible suffixes of a given string, sorted lexicographically.

Some common operations are: construction, searching, longest common prefix, counting distinct substrings etc.

Some real world applications are:

• Bio-informatics: Suffix arrays are used to search for patterns within DNA and protein sequences.
• Text search: These are used to search for text search and pattern finding algorithm. Eg: Boyer-Moore algorithm.
• Compression: Suffix arrays are used in data compression algorithm like LZ77 algorithm.
• Natural Language Processing: Suffix arrays are used in natural language processing to search for patterns within large texts.
• Databases: Suffix arrays are used in databases to index text fields for efficient searching and retrieval.

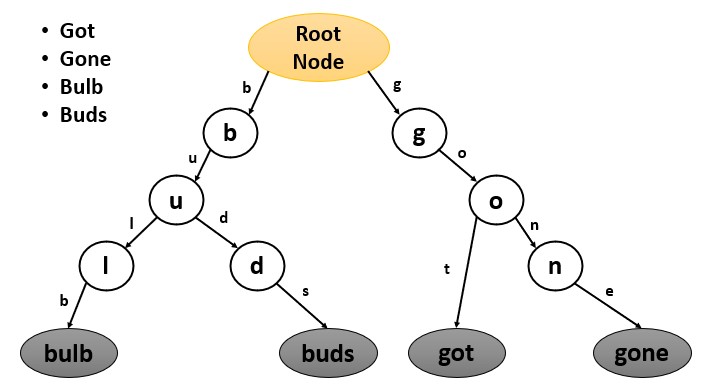
Trie

The need for trie arises from the requirement to effectively store and search for strings, where prefixes of the strings are also important. A trie (also called prefix tree), is a tree like data structure which can be used to store a collection of strings. Each node represents a character in a string, and the path from the root node to that node represents the a string in the collection.

Some common operations are: insertion, deletion, searching, prefix search, counting words, auto-complete etc.

Some real world applications are:

• IP Routing: Tries are used in IP routing to store and quickly look up routing tables.
• Text-editors: Tries are great for auto completing feature and are used in softwares like text editors.
• Compression: Tries are used in data compression algorithms like LZW algorithm.
• Spell checking: Tries are used in spell checkers to quickly look up words in a dictionary. This is being applied in many places in our daily lives.
• T9 Text Input: Tries are used to predict words based on a sequence of digit entered on a mobile phone keypad.

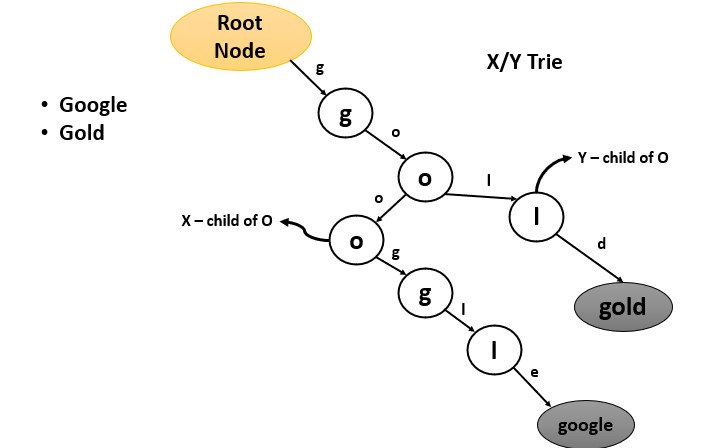
X/Y-Trie

We can use trie data structure for operations on strings, but when it came to storing multi-dimensional data such as points or rectangles in a 2D space we had no option to do that. This was why x/y trie data structure was introduced.

In x/y-trie, the root of the trie is the origin of the 2D space and each level in the trie corresponds to a different dimension. Each internal node of the trie is a split point, and the edges leaving the node represent the two subregions separated by the split point.

Some operations in x/y trie: insertion, searching, deletion, range queries, point location, nearest-neighbor point etc.

Some real-world applications are:

• Geographic information system: x/y tries are used in GIS, to efficiently store and search for spatial data such as points, lines, polygons etc.
• Computer vision: It can be used in computer vision for efficient image segmentation, object detection and image recognition.
• Robotics: It can be used in robotics for path planning, obstacle detection and image recognition.
• Gaming: Its used in games to efficiently search and locate objects in a virtual 2D or 3D world.
• VLSI Design: It can be used in VLSI design to store the layout information of a chip and perform geometric queries.

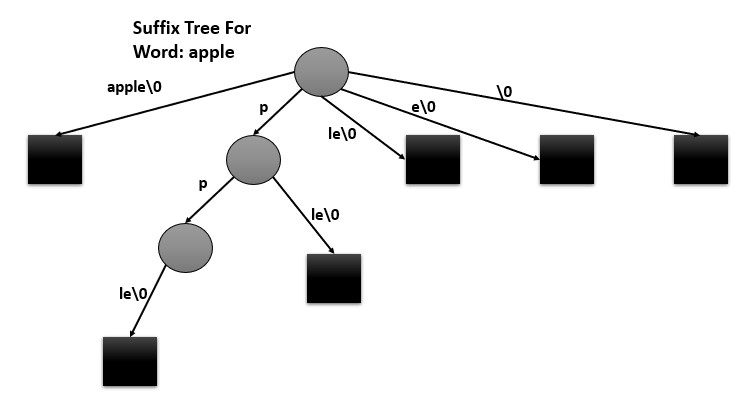
Suffix Tree

The need for a suffix tree arises from the requirement to efficiently search for patterns within a large text. A suffix tree is a data structure that is used to store all the possible suffixes of a given text, and it allows for efficient search for patterns within the text, with a time complexity of O(m) for searching, where m is the length of the pattern. A suffix tree is a compressed trie of all the suffixes of a given string. It is a space-efficient alternative to suffix arrays.

Some operations includes: construction, searching, longest repeated substring etc.

Some real-world applications are:

• Text search and pattern matching: suffix tree are used text search and pattern matching algorithms.
• Natural Language Processing: Suffix trees are used in natural language processing to search for patterns within large text corpora.
• Databases: Suffix trees are used in databases to index text fields for efficient searching and retrieval.
• Plagiarism Detection: Suffix trees are used to detect plagiarism in documents by identifying similar patterns.
• Bio-informatics: Suffix trees are used in bio-informatics to search for patterns within DNA and protein sequences.

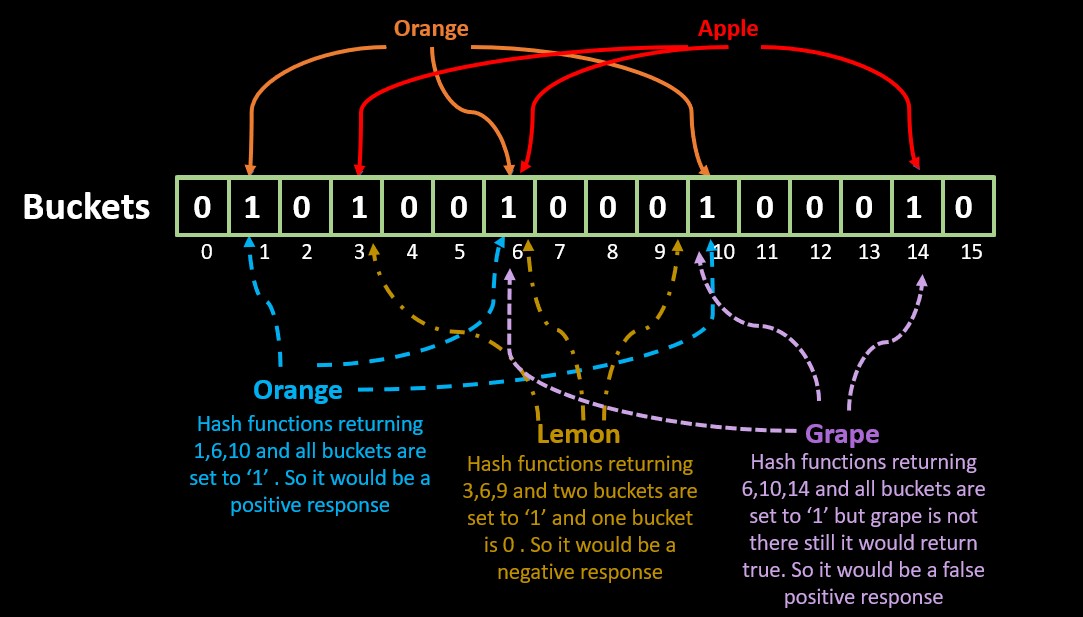
Bloom Filter

The need for a Bloom filter arises from the requirement to efficiently check if an element is a member of a set or not, when the set is too large to be stored in the memory. A Bloom filter is a probabilistic data structure that is used to test whether an element is a member of a set or not. It is a space-efficient data structure that uses a small amount of memory to store the set, but at the cost of a small probability of false positives (i.e., incorrectly reporting that an element is in the set when it is not).

Some common operations are: insertion, deletion member test.

Some real-world applications are:

• Network routers: They are used in network routers to efficiently check id a packet's destination address is in a routing table.
• Web browsers: Bloom filters are used in web browsers to check if a URL has been visited before.
• Spam filtering: Bloom filters are used in spam filtering to check if an email address is on a list of known spammers.
• Databases: They are used in databases to check if a key is in a set of keys, before performing a disk access.
• Cryptocurrency wallets: They are used to check of a transaction is relevant to specific wallet.

B-Tree

The need for a B-tree arises from the requirement to efficiently store and search large amounts of ordered data that doesn't fit in memory. B-tree is a self-balancing tree data structure that keeps data sorted and allows search, sequential access, insertion, and deletion operations with logarithmic time complexity.

Common operations are: insertion, searching, deletion, range queries, traversal etc.

Some real-world applications:

• File systems: B-trees are used in modern file systems, such as NTFS, ext4, and Btrfs, to index and organize large amounts of data.
• Database management systems: B-trees are used in database management systems, such as Berkeley DB and MySQL, to index and organize large amounts of data.
• B-trees are used in operating systems, such as Windows and Linux, to store and retrieve data from external storage devices.
• Search engines: B-trees are used in search engines, such as Lucene and Solr, to index and organize large amounts of text data.
• NoSQL databases: B-trees are used in NoSQL databases, such as MongoDB and Couchbase, to index and organize large amounts of data.

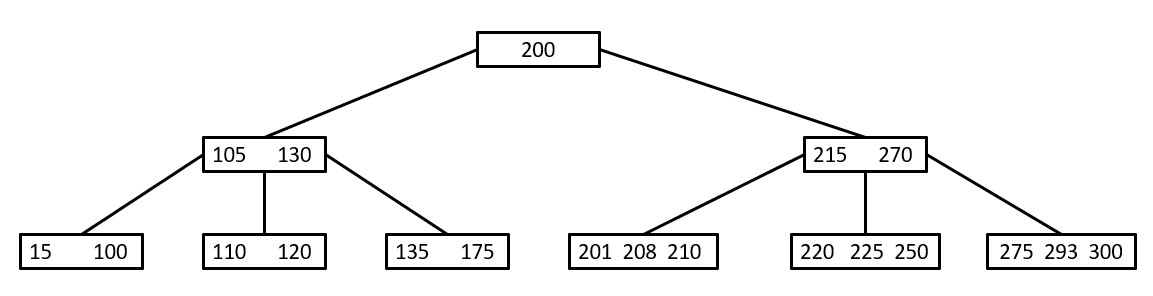
If you want to learn about B+ Trees and about its complexities click here.
If you want to learn about (a,b) trees click here.

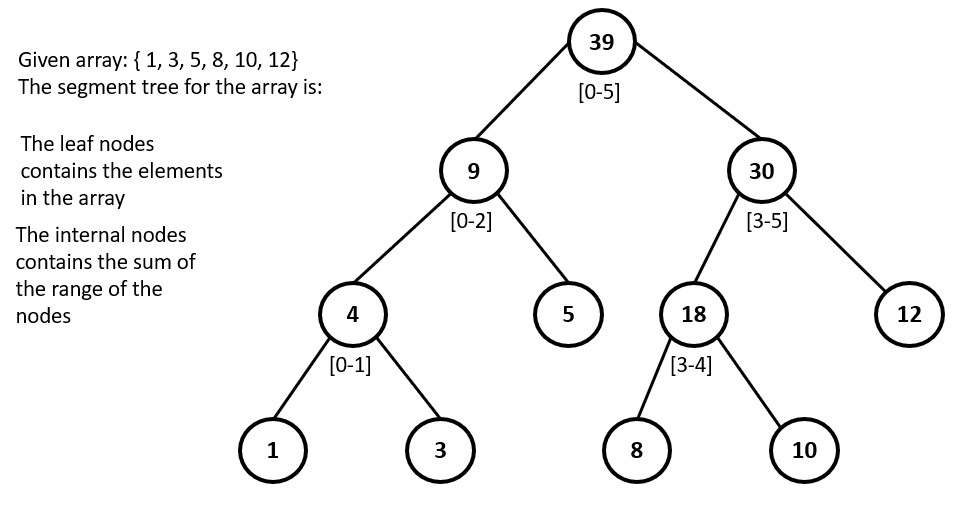
Segment Tree

The need for a Segment Tree arises from the requirement to efficiently perform operations such as range queries, range updates, and range minimum/maximum on an array of data. A Segment Tree is a data structure that can be used to perform these operations on an array in logarithmic time complexity. A segment tree represents a given array as a binary tree, where each leaf node represents an element of the array and each internal node represents a range of elements in the array.

Some common operations are: range query, range update, point update etc.

Some real-world applications:

• Range min/max query: Finding min/max element in a given range of an array.
• Range sum query: Finding the sum of all element in the given range.
• Range set/clear query: Setting/clearing elements in a given range of an array.
• Range gcd/lcm query: Finding the gcd/lcm of elements in a given range of an array.
• Dynamic programming: Segment trees can be used to store and update the state of dynamic programming solutions.

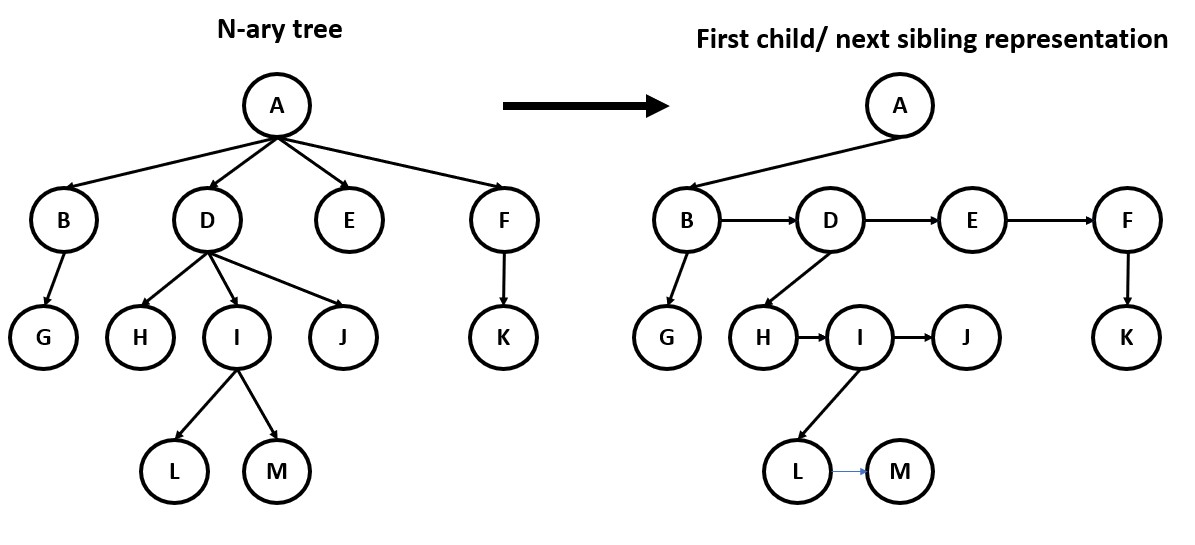
n-ary Tree

The need for a n-ary tree (Generic Tree) arises from the requirement to efficiently store and search hierarchical data structures where each node can have more than two children. An n-ary tree is a tree data structure where each node can have an arbitrary number of children, rather than the binary tree structure where each node can have at most two children.

Some common operations are: Insertion, traversal searching and deletion.

Some real-world applications are:

• File Systems: N-ary trees are used in some file systems to organize the hierarchical structure of folders and files.
• XML parsing: N-ary trees are used in parsing and storing XML data.
• Game Development: N-ary trees are used to represent games objects, such as levels and characters, in a game's scheme graph.
• Network routing: N-ary trees are used in some routing protocols to organize the hierarchical structure of a network.
• Natural Language Processing: N-ary trees are used to represent the syntactic structure of a sentence in natural language processing

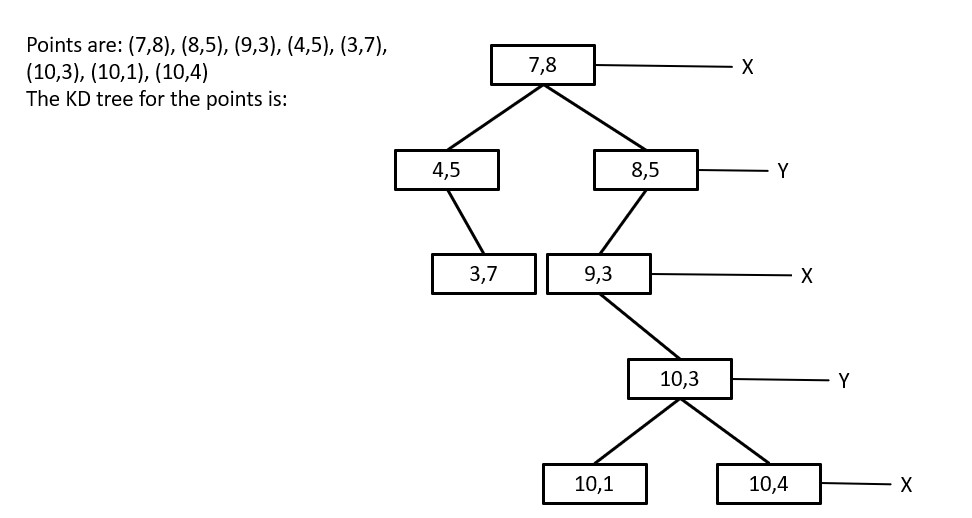
K-Dimensional Tree

The need for a k-dimensional tree arises from the requirement to efficiently perform operations such as search, nearest neighbor search, and range search on large multi-dimensional data sets.

A k-dimensional tree is a type of space-partitioning data structure used to organize points in a k-dimensional space. It is a generalization of a binary search tree, where each internal node in the tree represents a split in k-dimensional space, rather than just a split in one dimension as in a binary search tree.

Some common operations are: Insertion, searching, nearest neighbour search, range search etc.

Some real-world applications:

• Computer graphics: They are used in this filed for spatial partitioning, collision detection and visibility culling.
• Robotics: They are used in robotics for path planning, collision detection and localization.
• Image processing: K-dimensional trees are used in image processing for image segmentation and feature extraction.
• Machine learning: These trees used in machine learning for nearest neighbor classification and regression.
• Geographic Information Systems: These trees are used in GIS for spatial indexing and searching of large amounts of geospatial data.

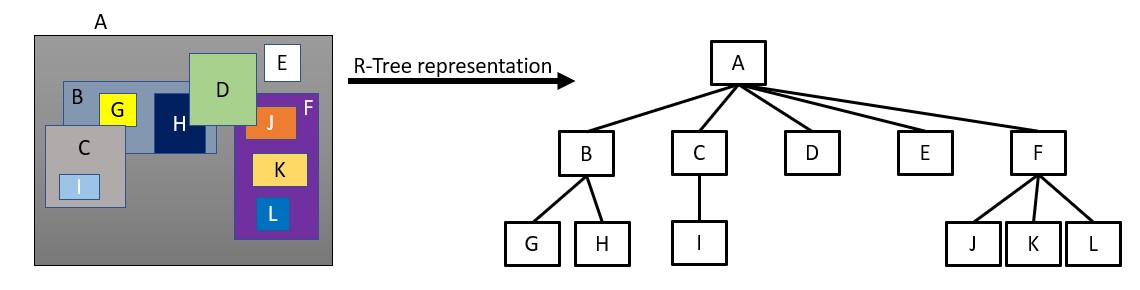
R-Tree

The need for an R-tree arises from the requirement to efficiently store and search large amounts of multidimensional spatial data, such as geographic coordinates or geometric shapes. An R-tree is a type of spatial indexing data structure that organizes data in a hierarchical tree structure based on their spatial relationships.

Some common operations are: insertion, deletion, searching, building, re-balancing.

Some real-world applications are:

• Geographic Information System: R-trees are used in GIS for spatial indexing and searching of large amounts of geospatial data.
• Computer Graphics: R-trees are used in computer graphics for spatial partition, visibility culling and collision detection.
• Robotics: R-trees are used in robotics for path planning and localization.
• Image Processing: R-trees are used in image processing for image segmentation and feature extraction.
• Databases: R-trees are used in databases to index and organize spatial data.

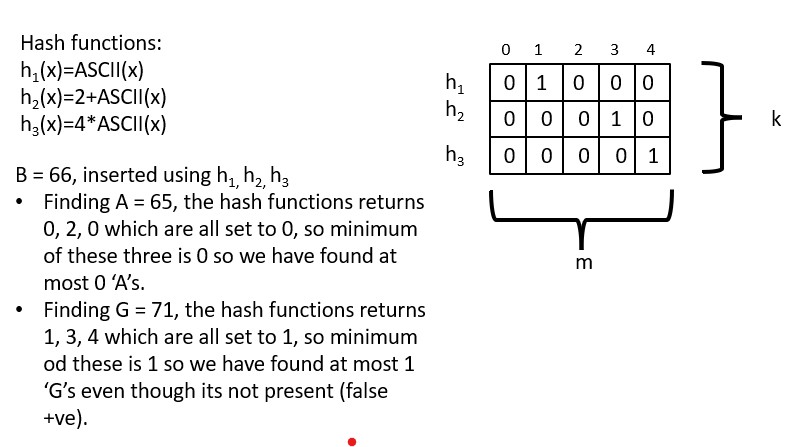
Count Min Sketch

The need for a Count Min Sketch arises from the requirement to estimate the frequency of elements in a large stream of data, such as a data feed or a log file, with a high degree of accuracy. Count Min Sketch is a probabilistic data structure that provides approximate answers to questions about the frequency of elements in a stream, using a small amount of memory. It is a useful data structure when it is impractical to keep an explicit count of all the elements in a stream, due to the large number of distinct elements or the high rate of incoming data.

Some common operations are: insertion, query, update, building etc.

Some real-world applications are:

• Anomaly detection: Count Min Sketch can be used to detect unusual patterns in a stream of data, such as a spike in traffic to a website or a surge in logins from a specific IP address.
• Network monitoring: Count Min Sketch can be used to monitor network traffic, such as counting the number of packets sent by a specific host or tracking the number of connections to a service.
• Natural Language Processing: Count Min Sketch can be used to estimate the frequency of words in large text corpora, such as counting the number of times a specific word appears in a set of documents.
• Streaming data analysis: Count Min Sketch can be used to estimate the frequency of different events in a stream of data, such as counting the number of unique visitors to a website.
• Machine learning: Count Min Sketch can be used to estimate the frequency of different classes in a dataset, such as counting the number of times a specific label appears in a set of examples.

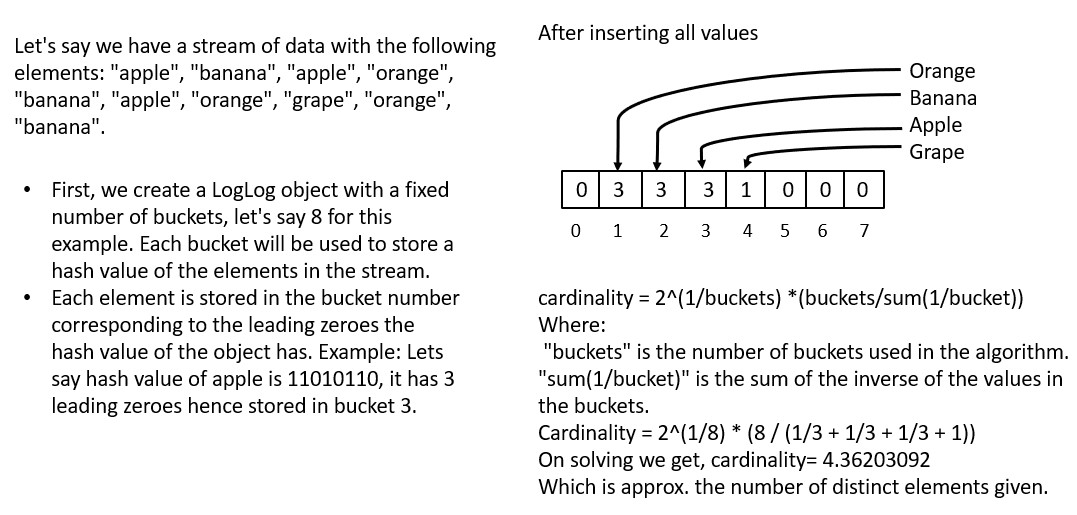
LogLog

The need for a LogLog algorithm arises from the requirement to estimate the number of distinct elements in a large stream of data, known as the "cardinality" of the set. LogLog is a probabilistic algorithm that uses a small amount of memory to estimate the cardinality of a set with a high degree of accuracy. It is particularly useful when the exact number of distinct elements is not needed, but only an approximation of it is required, or when the data is too large to store in memory.

Some common operation: insertion, cardinality, building.

Some real-world application:

• Network monitoring: LogLog can be used to estimate the number of unique number of IP address in a network traffic stream.
• Social network analysis: LogLog can be used to estimate the number of unique users in a social network.
• Web analytics: LogLog can be used to estimate the number of unique visitors to a website.
• Stream Processing: LogLog can be used to count unique elements in a stream of data, such as unique users or unique events.
• Fraud detection: LogLog can be used to count the number of unique credit card numbers that are used in a set of transactions to detect potential fraud.

Summary

S.No	Data Structure	Real-World Applications
1.	Arrays	Database indexing, image processing, game programming, sorting & searching, spreadsheets
2.	Matrix	Linear algebra, computer graphics, machine learning, robotics, cryptography
3.	Vectors	Physics, computer graphics, control systems, navigation, economics
4.	Strings	Text processing, web dev, database management, natural language, encryption & cryptography
5.	Linked List	OS, computer networks,game dev, compilers, music and audio software
6.	Stack	Computer science, web browsers, GUI, calculater & math softwares, computer networks
7.	Queue	OS, computer networks, simulation, transportation, gaming
8.	Binary Tree	File systems, game dev, decision making, data compression, natural language processing
9.	Binary Search Tree	Spell checker, file systems, computer networks, expression evalution, natural language processing
10.	Heap	Graph algorithm, OS, priority queue, huffman coding, medical treatment
11.	Hashing	Database indexing, cryptography, cache, data compression, network routing
12.	Graph	Social networks, GPS navigation, web search, biology, electric power grid
13.	Suffix Array	Bioinformatics, text search, data compression, natural language processing, databases
14.	Trie	IP routing, text editors, compression, spell checking, T9 text input
15.	X/Y-Trie	Geographic information system, computer vision, robotics, gaming, VLSI design
16.	Suffix Tree	Text search and pattern matching, natural language processing, databases, plagiarism, bio-informatics
17.	Bloom Filter	Network routers, web browsers, spam filtering, databases, cryptocurrency wallets
18.	B-Tree	File systems, database management systems, OS, search engines, NoSQL databases
19.	Segment Tree	Range min/max query, range sum query, range set/clear query, range gcd/lcm query
20.	n-ary Tree	File systems, XML parsing, game dev, network routing, natural language processing
21.	K-Dimensional Tree	Computer graphics, robotics, image processing, machine learning, geographic information systems
22.	R-Tree	Geographic information system, computer graphics, robotics, image processing, databases
23.	Count Min Sketch	Anomaly detection, network monitoring, natural language processing, streaming data analysis, machine learning
24.	LogLog	Network monitoring, social network analysis, web analytics, stream processing, fraud detection

Now you have reached the end of this article. Now you will be having the knowledge of different data structures, why it was introduced, different operations, real-world applications and its representation.