R-tree is an advanced height-balanced Tree Data Structure that is widely used in production for spatial problems (like geographical map operations). We have presented the need for R Tree along with the basics of R Tree so you can use it to solve problems as well.

Table of content:

1. Introduction / Why is there a need for R Tree?
2. So what are R-trees?
3. Implementation details of R Tree
4. Insertion in R Tree
5. Searching in R Tree

Introduction / Why is there a need for R Tree?

Spatial data can be defined as any data that points to specific location on Earth. Very often, these objects represent multi dimensional spaces that aren't well represented by point locations such as census tracts, countries as they occupy regions of non-zero size.

This data is stored in a database. And common operations for any database are storing data and performing all sorts of queries among others.
An example of a query or a real world problem is to find all the restaurants within 20 miles of a particular area.

These kind of operations are seen in CAD(Computer Aided Design) and geo-spatial applications. For a real-time application, there will be multiple queries as such performed per second. And this can be very time consuming and not very cost efficient if the database isn't designed optimally. Hence the database is required be designed in an efficient way in order to reduce the time taken for storing and querying.

Although there are many indexing based mechanisms such as B-trees and ISAM indexes, they won't work well with multi-dimensional data. Therefore, a data structure is required that can work in multi-dimensions and also is quick with the entire indexing part. Hence R-trees are used.

So what are R-trees?

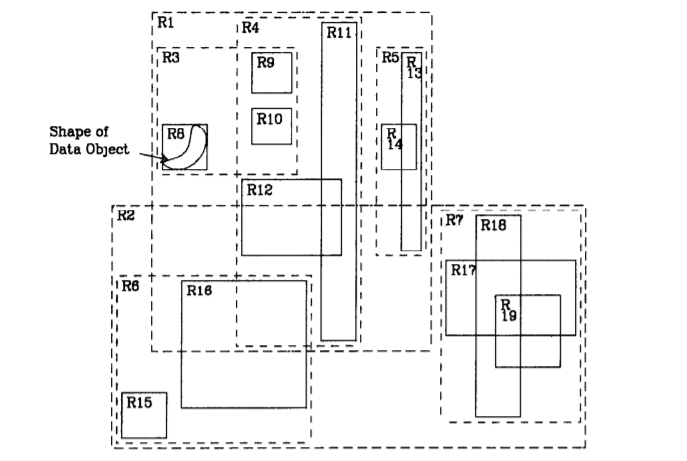
Before going to R-trees, there is one more thing to know which is MBR(Minimum Bounding Rectangles. This term is used to refer a geographical feature or a dataset, for spatial query purposes.

It generally is a 2D object (polygon, point, line) or a set of objects within its 2D x-y coordinate system which is the smallest bounding for a set of points in N-dimensions within which all the points lie.

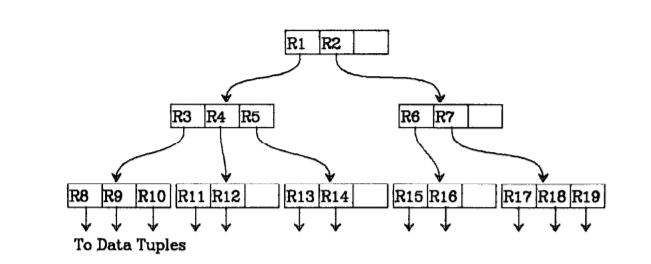
An R-tree is a height-balanced tree with index records in it's leaf nodes containing pointers to data objects Nodes correspond to disk pages if the index is disk-resident, and the structure is designed so that a spatial search requires visiting only a small number of nodes The index is completely dynamic;
inserts and deletes can be intermixed with searches and no periodic re-organization is required.

Implementation details of R Tree

A spatial database consists of a collection of tuples representing spatial objects, and each tuple has a unique identifier which can be used to retrieve it.
Leaf nodes in an R-tree contain index record entries of the form

(I, tuple_identifier)

A tuple in a database is referred to as a tuple_identifier and I represents n-dimensional rectangle which is the bounding box of the spatial object indexed.

I = (I0, I1, I2, .... In-1)      

where n represents the number of dimensions and Ii represents a close bounded interval [a,b] describing the extent of object along the dimension i.

Non-leaf nodes contain entries of the form

(I, child_pointer)

where child pointer is the address of a lower node in the R-tree and I covers all rectangles in the lower node’s entries.

Let M be the maximum number of entries that a node can acommodate and m (m <= M/2) be the parameter specifying the minimum number of entries, then an R-tree satisfies the following properties

1. Every leaf node contains nodes between m and M unless the root
2. For each index record( I, tuple identifier) in a leaf node, I is the smallest rectangle that spatially contains the n-dimensional data object represented by the indicated tuple.
3. Every non-leaf node has between m and M children unless it's the root.
4. For each entry (I, child pointer) in a non-leaf node, I is the smallest rectangle that spatially contains the rectangles in the child nodes=
5. The root node has at least two children unless it's a leaf
6. All leaves appear on the same level

The structure of an R-tree and the illustration of the containment and overlapping relationships that exist between the rectangles is given below.

The height of an R-tree containing N index records is at most |logm N| -1 as m is the minimum branching factor of each node.

The maximum number of nodes is ceil(N/m) + ceil(N/m^2) + 1

The worst case space utilization of for all the nodes except the root is m/M

If the nodes will have more than m entries then this will decrease the tree height and improve space utilization. The parameter m can be varied as a part of performance tuning.

Given a basic introduction to R-trees, in the upcoming sections insertion, deletion and searching will be discussed

Insertion in R Tree

New index records are added at the leaves and nodes that overflow(>M) are split. In this section we will be discussing how the generic insertion works and the two techniques for node splitting which are the "Exhaustive Algorithm" and the "Quadratic Search Algorithm".

Algorithm Insert

Insert a new index entry E into an R-tree. The algorithm first checks in which leaf the new entry must be placed and checks if that has enough space; if it does then it inserts else node splitting happens. After this all is done the changes are propogated upwards and if this causes the root to split then a new root is created.

1.Find position for new record Invoke ChooseLeaf to select a leaf node L in which to place E.
2.Add record to leaf node If L has large room for another entry then install E, else invoke SplitNode to obtain L and LL (current leaf and new leaf containing all old entries of L)
3.Propogate changes upward Invoke AdjustTree on L also passing LL if split was performed
4.Grow the tree taller If node split propogation caused the root to split, create a new root whose children are the two resulting nodes.

Algorithm ChooseLeaf

Select a leaf node in which to place a new entry E

1. Initialize Set N to be the root node
2. Leaf Check If N is a leaf, return N
3. Choose subtree If N is not a leaf, let F be the entry in N whose rectangle F1 needs least enlargement to include E1. Resolve ties by choosing the entry with the rectangle of smallest area
4. Descend until leaf is reached Set N to be child node pointed to by Fp and reoeat from step 2

Algorithm AdjustTree

The leaf nodes hold indexes that point to some data in the disk, if, due to the new entry the leaf nodes get split up then this information has to be updated in the parent nodes and this has to go all the way up to the root.

1. Intialize Set N=L (L being the leaf node) If L was split previously, set NN to be the resulting second node
2. Check if done If N is the root, stop
3. Adjust covering rectangle in parent entry Let P be the parent node of N, and let EN be N’s entry in P. Adjust EN I so that it tightly encloses all entry rectangles in N.
4. Propagate node split upward If N has a partner NN resulting from an earlier split, create a new entry ENN with ENNp pointmg to NN and ENN I enclosing all rectangles in NN. Add ENN to P If there is room. Otherwise, invoke SplitNode to produce P and PP contining ENN and all P’s old entries.
5. Move up to next level Set N=P and set NN=PP If a split occurred. Repeat from step 2.

Node Splitting

If a node already has M entries, then to add a new entry this node (M+1 entries) has to be divided into two. Now, this division should happen in such a way that the total area of the covering rectangle should be minimised, i.e the division should be done in such a way that it becomes very unlikely that both the new nodes will be examined on subsequent searches. This is because the decision whether to visit a node depends on whether it's covering rectangle overlaps the search area, hence the total area of the two covering rectangles should be minimized.

Good v/s Bad Split

The difference between a bad split (a split that has more area) and a good split(comparitively lesser area).

The same criterion was used in ChooseLeaf to decide where to insert a new index entry at each level in the tree, the subtree that was chosen was the one whose covering rectangle would have to be enlarged least.

Three algorithms will be discussed here which are

1. Exhaustive Algorithm
2. Quadratic-Cost Algorithm
3. Linear-Cost Algorithm

Exhaustive Algorithm
The most straightforward way to solve the problem is to generate all possible groupings and choose the one that not only suits the criterion, but is also the best.

This means generating 2^(M-1) possibilities; even for a reasonable M value such as 50, the time complexity is very large.

Quadratic-Cost Algorithm
This algorithm does give a small area, but it doesn't guarantee it to be the best.

Searching in R Tree

The structure of the tree is not similar to the traditional binary search trees, there might be more than one subtrees for a node corresponding to the indices. Although seaching will begin from the root, the worst case complexity is not guaranteed.

Nevertheless with most kinds of data the update algorithms will maintain the tree in a form that allows the search algorithm to eliminate irrelevant regions of the indexed space, and examine only data near the search area.

With this article at OpenGenus, you must have the basic idea of R Tree. You can go deeper to contruct the complete search operation and delete operation on your own easily. Try it.