
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
The objective of this OpenGenus article is to explore the concept of utilizing anagram trees, a specialized tree structure, to efficiently organize and retrieve anagrams of words.
Table of Contents:
- What are anagram trees?
- Using anagram trees to retrieve anagrams
- Implementation through code
- Anagram Trees Operations
- Real life applications
- Key takeaways
- Questions
- References
What are anagram trees?
Before defining what an anagram tree is, I think it's important to understand what the words 'anagram' and 'trees' respectively mean.
Anagrams:
An anagram is a word or phrase formed by rearranging the letters of another. For example, "listen" and "silent" are anagrams of each other. In the context of data structures, dealing with anagrams often involves manipulating strings or characters and checking whether they can be rearranged to form another word.
Trees:
Trees are a fundamental data structure in computer science. They consist of nodes connected by edges, where each node can have zero or more child nodes. Trees have various types, such as binary trees, AVL trees, and B-trees, among others. Trees are widely used for organizing and storing data efficiently, with applications in search algorithms, file systems, and hierarchical structures.
Now that there is an understanding of what the words are separately, I will go ahead and define what anagram trees are.
Anagram trees refer to a data structure used to efficiently store and retrieve anagrams. For instance, a tree structure could be used to organize words based on their letter combinations.
Using anagram trees to retrieve anagrams.
Below is a diagram of an anagram tree constructed from the combination of the letters A,R,E. The structure of the tree follows the normal structure of a tree by including the root node,child nodes, edges as well as leaves. The tree has three attributes being a letter from the combination of words, indicated on each node, the number of occurrances, indicated on the edges and a list of anagrams on the leaves.
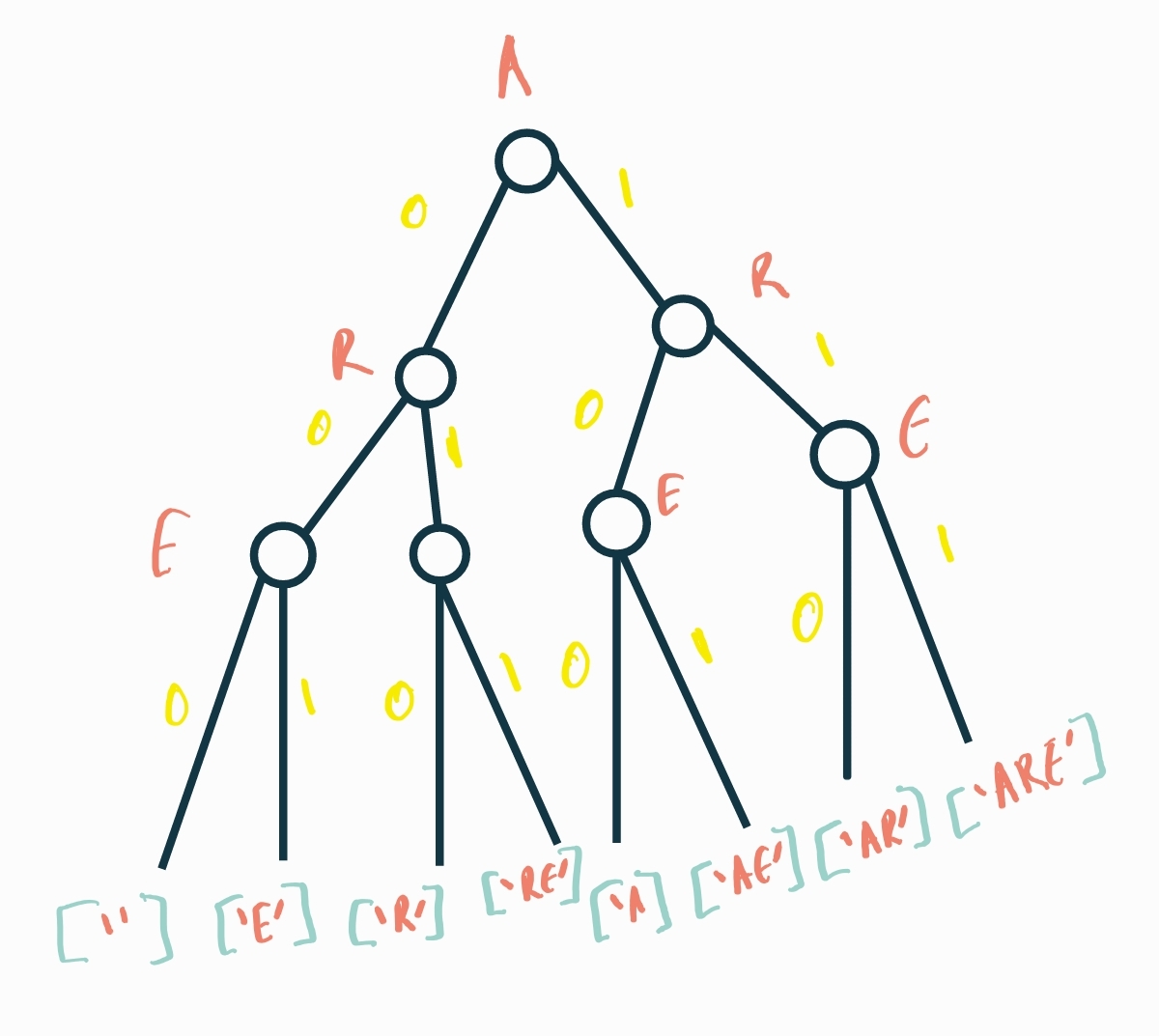
The tree helps us determine all the new words/combinations that can be formed based on the occurrences. For example, if we wanted to retrieve a word that has no occurence of A, we would only be able to retrieve a word with occurances of E and/or R.
In the case of the string 'ARE', we have can either retrieve anagrams with all letters in the string occurring in the anagrams, two letters from the string occurring or only one letter from the string occuring.
Implementation through code
The implementation of the code is as follows:
from itertools import permutations
class ParentAnagramTree:
def __init__(self, word):
self.word = word
self.node = ''
self.leaves = []
class ChildAnagramTree(ParentAnagramTree):
def __init__(self, word):
super().__init__(word)
self.leaves = generate_leaves(self.node, self.word)
self.anagrams = all_anagrams(self.leaves)
def generate_leaves(node, word):
if len(word) == 0:
return ['']
node = word[0]
string = generate_leaves(node,word[1:])
leaves = []
for combination in string:
leaves.append(combination)
leaves.append(node + combination)
return leaves
def all_anagrams(leaves):
anagram_list = []
for i in leaves:
if i != '':
l = permutations(i)
for j in l:
anagram_list.append(''.join(list(j)))
return sorted(set(anagram_list))
new_tree = ChildAnagramTree('ARE')
print(new_tree.anagrams)
'''OUTPUT:
['A', 'AE', 'AER', 'AR', 'ARE', 'E', 'EA', 'EAR', 'ER', 'ERA', 'R', 'RA', 'RAE', 'RE', 'REA']'''
Here's a more detailed explaination of the above code:
- ParentAnagramTree Class:
This class is a basic tree structure with attributes word, node, and leaves. It is intended to be a parent class for an anagram tree.
- ChildAnagramTree Class (Inherits from ParentAnagramTree):
This class extends ParentAnagramTree and adds two attributes: leaves and anagrams.The init method initializes the parent class and then sets self.leaves by calling the generate_leaves function with self.node and self.word. Finally, it sets self.anagrams by calling the all_anagrams function with self.leaves.
- generate_leaves Function:
This recursive function generates all possible combinations of letters from the given word.It starts with an empty string node and appends each letter to the combinations, creating a tree structure.The base case is when the length of the word becomes zero, and it returns a list containing an empty string.
- all_anagrams Function:
This function takes a list of leaves and generates all possible anagrams by permuting the letters in each leaf using itertools.permutations. The resulting list of anagrams is sorted, and duplicates are removed using set.
- Instance Creation and Output:
An instance of ChildAnagramTree is created with the word 'ARE'.
The print(new_tree.anagrams) statement outputs a sorted list of unique anagrams of the word 'ARE'.
Complexity:
- ParentTree Class:
Time Complexity:
The initialization of the ParentTree class involves assigning values to attributes, which are simple operations. The time complexity of the init method is constant, O(1)O(1).
Space Complexity:
The space complexity of the ParentTree class is determined by the attributes it holds (word, node, and leaves). The space required for each instance of the class is constant, O(1)O(1).
- ChildAnagramTree Class (Inherits from ParentTree):
Time Complexity:
The initialization of the ChildAnagramTree class involves calling the init method of the parent class (ParentTree) and then calling the generate_leaves and all_anagrams functions. The time complexity of the init method is O(1)O(1) (constant) for the parent class initialization, and the time complexity is O(2n+m⋅n!)O(2n+m⋅n!) for the generate_leaves and all_anagrams functions.
Space Complexity:
The space complexity of the ChildAnagramTree class is determined by the attributes it holds (word, node, leaves, and anagrams). The space required for each instance of the class is O(2n+m⋅n!)O(2n+m⋅n!), where nn is the length of the word, mm is the number of leaves, and nn is the maximum length of a leaf.
Anagram Trees Operations
Just like any other data structure, there are multiple operations that can be performed on Anagram Trees, such as inserting, deleting, searching as well as updating. Below I demostrated through code how you could do operations on an anagram tree. Do note the this follows from the previous code implementation.
def insert_letter(self, letter, position):
split_word = [char for char in self.word]
split_word.insert(position, letter)
self.word = ''.join(split_word)
return ChildAnagramTree(self.word)
def delete_letter(self,position):
split_word = [char for char in self.word]
split_word.pop(position)
self.word = ''.join(split_word)
return ChildAnagramTree(self.word)
def replace_letter(self, letter, position):
split_word = [char for char in self.word]
split_word[position] = letter
self.word = ''.join(split_word)
return ChildAnagramTree(self.word)
def search_valid_words(self):
library = ['ARE', 'ERA', 'EAR']
valid = [i for i in self.anagrams if i in library]
return valid
new = ChildAnagramTree('ARE')
new = new.insert_letter('A',3)
print(new.anagrams)
'''OUTPUT:
['A', 'AA', 'AAE', 'AAER', 'AAR', 'AARE', 'AE', 'AEA', 'AEAR', 'AER', 'AERA', 'AR', 'ARA', 'ARAE', 'ARE',
'AREA', 'E', 'EA', 'EAA', 'EAAR', 'EAR', 'EARA', 'ER', 'ERA', 'ERAA', 'R', 'RA', 'RAA', 'RAAE', 'RAE', 'RAEA', 'RE',
'REA', 'REAA']
'''
print(new.search_valid_words())
'''OUTPUT:
['ARE', 'EAR', 'ERA']
'''
Here's a an explaination of the above methods:
- insert_letter method:
This method is used to insert a letter at a specified position in the tree. It returns a new instance of the ChildAnagramTree with the modified tree.
- delete_letter method
This method deletes a letter at the specified position in the tree. Similar to insert_letter, it returns a new ChildAnagramTree instance with the modified tree.
- replace_letter method
This method replaces a letter at the specified position with the given letter. It again returns a new ChildAnagramTree instance with the modified tree.
- search_valid_words method
This method searches for valid words among the generated anagrams. It has a hardcoded library list containing valid words. It checks each generated anagram and includes it in the result only if it is found in the library. The result is a list of valid words.
Complexity:
1.insert_letter method
Time Complexity: O(N)
- Converting the word into a list of characters takes O(N) time, where N is the length of the word.
- Inserting a letter into the list takes O(1) time.
- Joining the list back into a string takes O(N) time.
Space Complexity: O(N)
- The space complexity is dominated by the list created from the word.
- delete_letter method
Time Complexity: O(N)
- Converting the word into a list of characters takes O(N) time, where N is the length of the word.
- Removing a letter from the list takes O(1) time.
- Joining the list back into a string takes O(N) time.
Space Complexity: O(N)
- The space complexity is dominated by the list created from the word.
3.replace_letter method
Time Complexity: O(N)
- Replacing a letter in a list takes constant time.
- No need to convert the word to a list or join it back.
Space Complexity: O(N)
- The space complexity is dominated by the list created from the word.
- search_valid_words method
Time Complexity: O(K * M)
- Where K is the number of anagrams and M is the average length of the anagrams.
- Checking if each anagram is in the library takes O(M) time.
Space Complexity: O(K)
- Where K is the number of valid words found.
- The space complexity is dominated by the list of valid words.
Real life applications
Anagram trees have the following real life applications.
-
Word Games and Puzzles: Anagram trees or algorithms can be employed in word games and puzzles, such as Scrabble or crossword puzzles, to find and verify possible word combinations.
-
Cryptography: Anagrams and permutations play a role in certain cryptographic techniques. For example, anagram-based ciphers might involve rearranging letters to encrypt or decrypt messages.
-
Data Compression: Anagrams could be used as a basis for encoding schemes in data compression algorithms, where words or phrases are represented by shorter codes.
-
Text Analysis and Natural Language Processing (NLP): Anagram trees can be applied in text analysis and NLP to identify anagrams or related words, which might be useful for understanding language patterns or sentiment analysis.
-
Educational Tools: Anagram trees can be used in educational tools to help students practice and learn vocabulary. Interactive applications could generate anagrams for a given set of letters, helping users expand their word knowledge.
-
Code Optimization: In code optimization, anagrams might be used in certain algorithms or data structures to efficiently search for optimal solutions or arrangements of elements.
-
Crossword Puzzle Solvers: Anagram trees can assist in solving crossword puzzles by quickly identifying potential word combinations that fit into given spaces.
-
Biological Sequence Analysis: In bioinformatics, anagram-like structures can be used in the analysis of biological sequences, where rearrangements of genetic elements or proteins need to be considered.
Key-takeaways
- Anagram trees can be used to efficiently retrieve anagrams of a given set of letters. The tree structure helps identify word combinations based on occurrences of specific letters.
- Anagram trees can be manipulated through adding, deleting, replacing and searching for data.
- Anagram trees find applications in various real-life scenarios, including word games, cryptography, data compression, text analysis, educational tools, code optimization, crossword puzzle solving, and biological sequence analysis.
