
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 16 minutes
An AVL Tree (Adelson-Velsky and Landis tree) is a self balancing binary search tree such that for every internal node of the tree the heights of the children of node can differ by at most 1. If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using rotation techniques.
The credit of AVL Tree goes to Georgy Adelson-Velsky and Evgenii Landis.
Every node in an AVL tree has a number known as balance factor associated with it.
BalanceFactor = height of right-subtree − height of left-subtree
In an AVL Tree, balance_factor is an integer from the set {-1, 0, 1}. If it is different from the three integers, the tree needs to be balanced using techniques we will discuss further in this article.
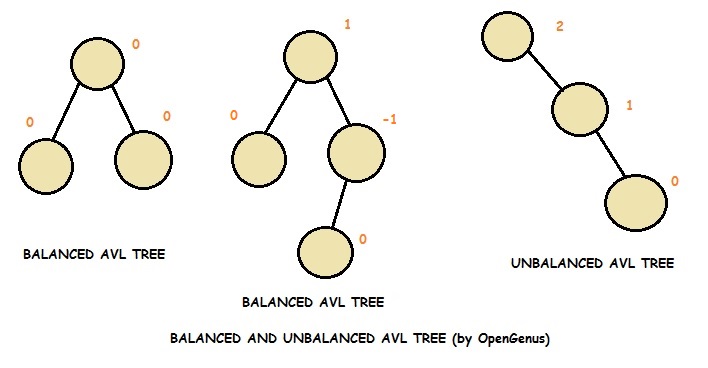
To make itself balanced, an AVL tree may perform four kinds of rotations:
- Left rotation (LL Rotation)
- Right rotation (RR Rotation)
- Left-Right rotation (LR Rotation)
- Right-Left rotation (RL Rotation)
Left rotation (LL Rotation) and Right rotation (RR Rotation) are single rotations while Left-Right rotation (LR Rotation) and Right-Left rotation (RL Rotation) are double rotations.
Following are the details regarding the various rotation techniques employed by AVL tree:
1.Left Rotation
A left rotation is a balancing technique that is applied on an unbalanced AVL Tree on a node having the balance_factor > 1. The unbalance property can be triggered by an insertion or deletion in a balanced AVL Tree.
In Left Rotation, every node moves one position to left from the current position.
Consider the following example:
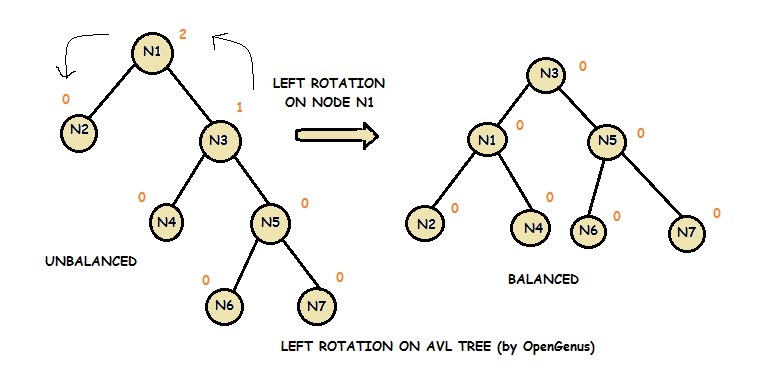
Notice that node N3 takes the place of node N1. N1 takes the place of node N2 and becomes the left child of node N3. Node N2 becomes the left child of node N1. Node N4, which was the left child of node N3, becomes the right child of node N1.
Note that nodes N2 and N4 can be replaced by subtrees.
This operation takes O(log N) time complexity in the worst case scenario.
2.Right Rotation
A right rotation is a balancing technique that is applied on an unbalanced AVL Tree on a node having the balance_factor < -1. The unbalance property can be triggered by an insertion or deletion in a balanced AVL Tree.
In Right Rotation, every node moves one position to right from the current position.
Consider the following example:
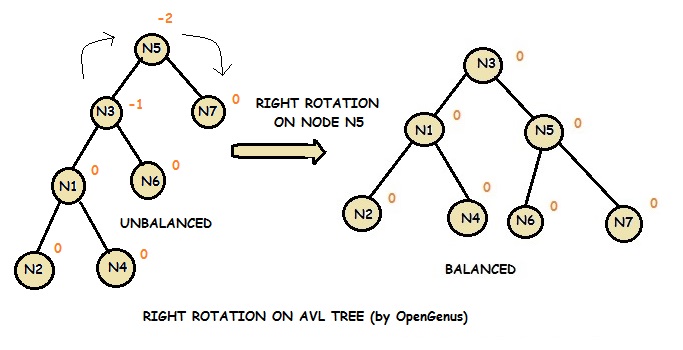
Notice that node N3 takes the place of node N5. N1 takes the original place of node N3 and becomes the left child of node N3. Node N6, which was the right child of node N3, becomes the left child of node N5.
Note that nodes N1 and N6 can be replaced by subtrees.
This operation takes O(log N) time complexity in the worst case scenario.
3.Left Right Rotation
The Left Right Rotation is combination of single left rotation followed by single right rotation. In LR Roration, first every node moves one position to left then one position to right from the current position.
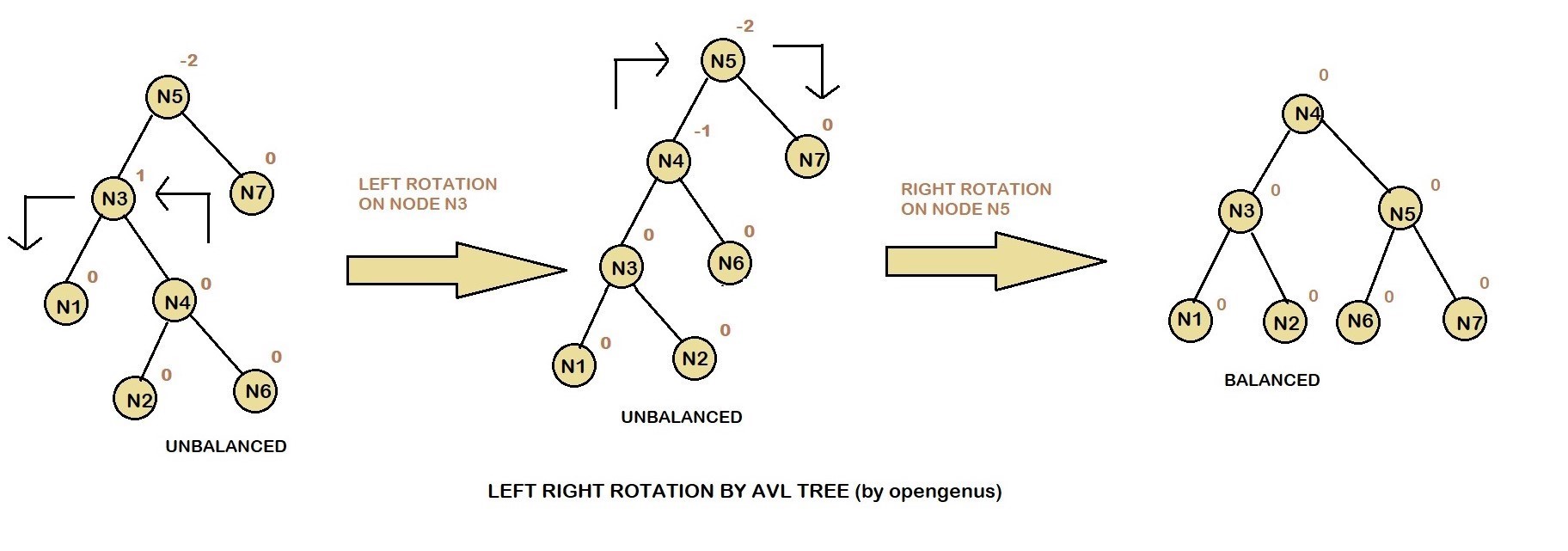
4.Right Left Rotation
The Right Left Rotation is combination of single right rotation followed by single left rotation. In RL Roration, first every node moves one position to right then one position to left from the current position.
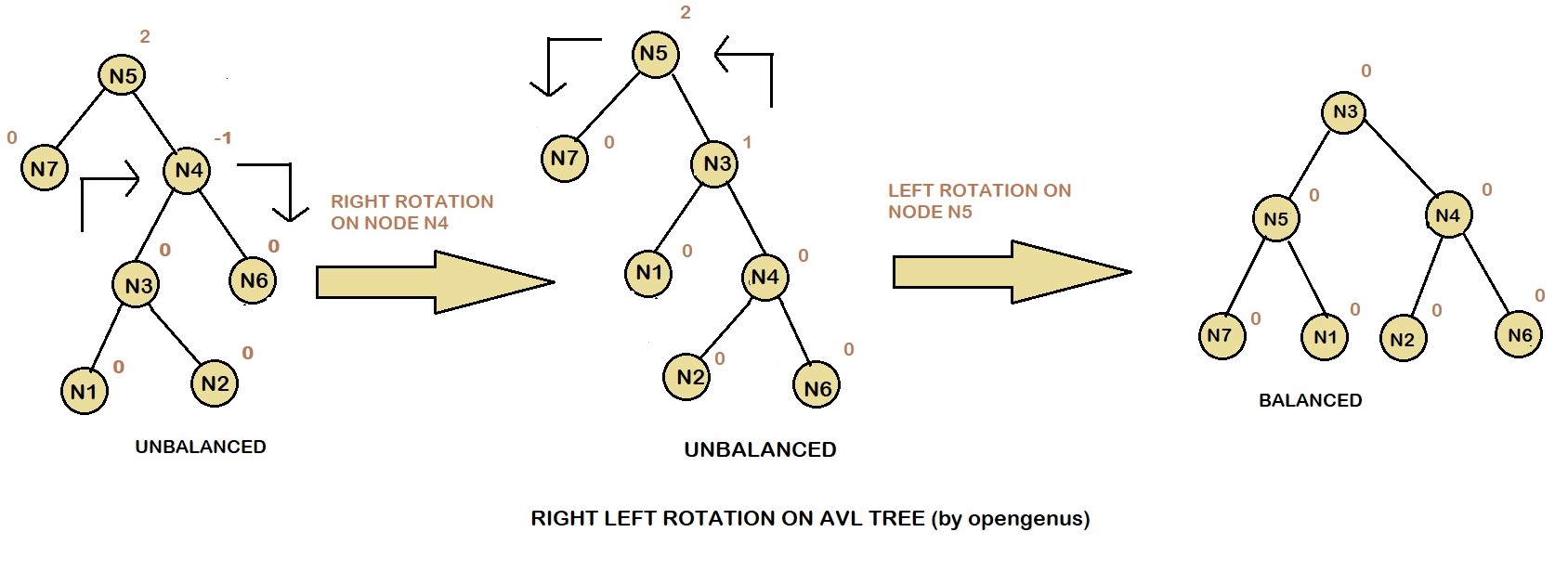
How to choose a particular rotation?
A tree rotation is necessary when you have inserted or deleted a node which leaves the tree in an unbalanced state. An unbalanced state is defined as a state in which any subtree has a balance factor of greater than 1, or less than -1. That is, any tree with a difference between the heights of its two subtrees greater than 1, is considered unbalanced.
-
Get the balance factor (left subtree height – right subtree height) of the current node.
-
If balance factor is greater than 1, then the current node is unbalanced and we are either in Left case or left Right case. To check whether it is left case or not, compare the newly inserted key with the key in left subtree root.
-
If balance factor is less than -1, then the current node is unbalanced and we are either in Right case or Right Left case. To check whether it is Right case or not, compare the newly inserted key with the key in right subtree root.
Pseudocode
Pseudocode of AVL Tree insert operation is as follows:
* Insert as in a Binary Search Tree.
* Check back up path for imbalance, which will be 1 of 4 cases:
1. node’s left-left grandchild is too tall
2. node’s left-right grandchild is too tall
3. node’s right-left grandchild is too tall
4. node’s right-right grandchild is too tall
* Only one case occurs because tree was balanced before insert
* After the appropriate single or double rotation:
* the smallest unbalanced subtree has the same height as before the insertion
* So all ancestors are now balanced
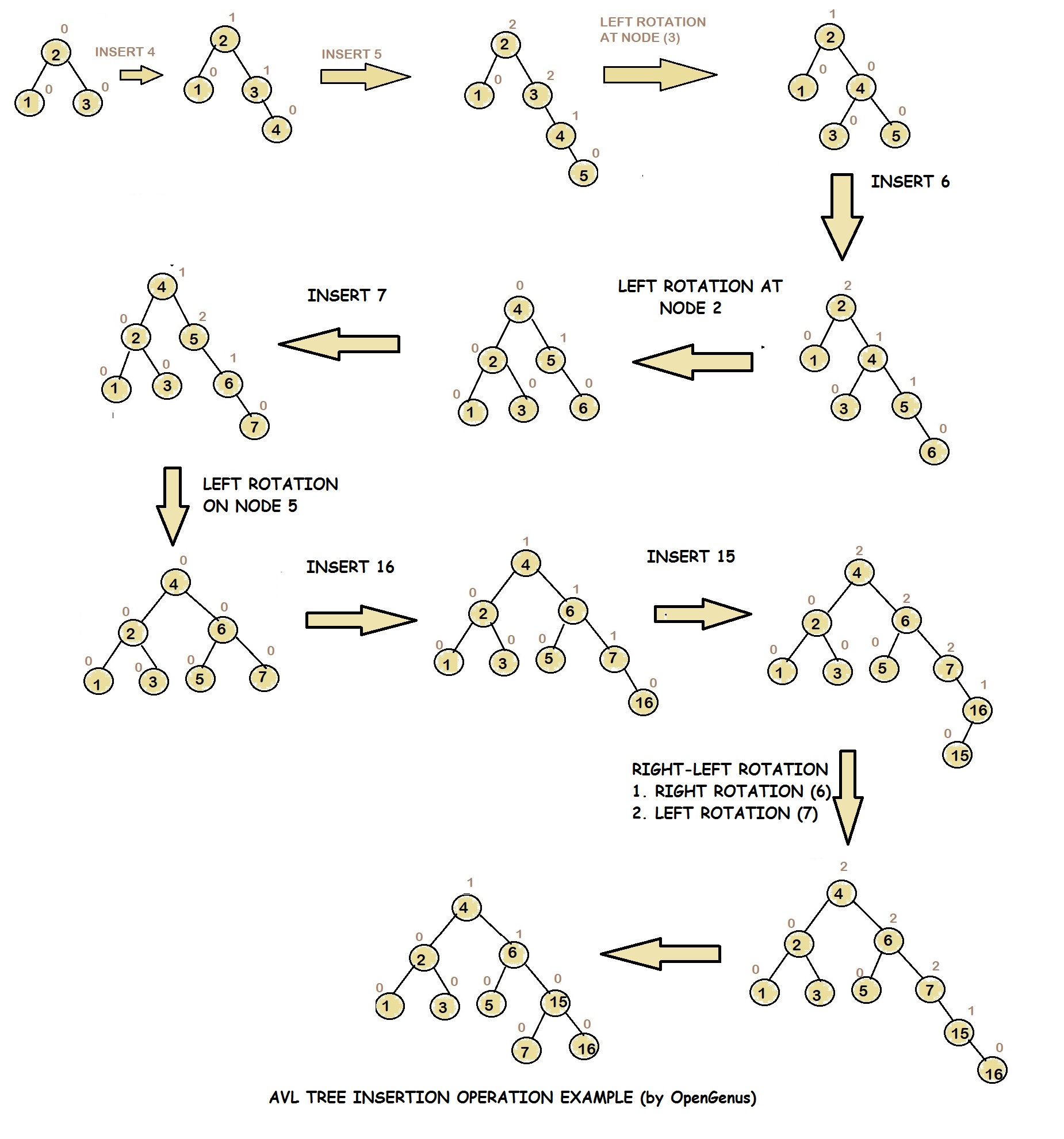
Example:
This is an example of building an AVL Tree by inserting 4,5,6,7,16 and 15 sequentially to an, initially, balanced binary search tree with 3 nodes (1,2,3)):
Complexity
- Worst case time complexity for search operation:
Θ(log N) - Worst case time complexity for insert operation:
Θ(log N) - Worst case time complexity to build tree :
Θ(N log N)
Implementations
- C++
C++
// AVL Tree - Insertion
//Part of Cosmos by OpenGenus Foundation
#include <iostream>
#include <algorithm>
struct Node
{
int _data;
Node *left;
Node *right;
int _height;
};
class AvlTree
{
private:
static Node *root;
public:
Node *NewNode (int key)
{
Node *temp=(Node*) malloc (sizeof(Node));
temp->_data=key;
temp->left=temp->right=nullptr;
return temp;
}
int Height (Node*node)
{
if (node==nullptr)
return 0;
int lh=Height(node->left);
int rh=Height(node->right);
if (lh > rh)
return lh+1;
else
return rh+1;
}
int getBalance (Node *node)
{
if (node==nullptr)
return 0;
return Height(node->left) - Height(node->right);
}
Node *getRightRotate (Node *y)
{
Node *x=y->left;
Node *T2=x->right;
x->right=y;
y->left=T2;
y->_height=std::max(Height(y->left) , Height(y->right))+1;
x->_height=std::max(Height(x->left) , Height(x->right))+1;
return x;
}
Node *getLeftRotate (Node *x)
{
Node *y=x->right;
Node *T2=y->left;
y->left=x;
x->right=T2;
x->_height=std::max(Height(x->left),Height(x->right))+1;
y->_height=std::max(Height(y->left),Height(y->right))+1;
return y;
}
Node* insertToAVL (Node*node, int _data)
{
if(node==NULL)
return NewNode(_data);
if(_data < node->_data)
{
node->left=insertToAVL(node->left,_data);
}
else if(_data > node->_data)
{
node->right=insertToAVL(node->right,_data);
}
else
{
return node;
}
node->_height=1+std::max(Height(node->left),Height(node->right));
int balance = getBalance(node);
//left left rotation
if(balance > 1 && _data < node->left->_data)
{
return getRightRotate(node);
}
// right right rotation
if(balance < -1 && _data > node->right->_data)
{
return getLeftRotate(node);
}
//left Right Rotation
if(balance > 1 && _data > node->left->_data)
{
node->left=getLeftRotate(node->left);
return getRightRotate(node);
}
//Right Left Rotation
if(balance < -1 && _data < node->right->_data)
{
node->right=getRightRotate(node->right);
return getLeftRotate(node);
}
return node;
}
void InOrder (Node *root)
{
if(root != NULL)
{
InOrder(root->left);
std::cout<<root->_data<<" ";
InOrder(root->right);
}
}
};
int main()
{
int Choice , Key;
AvlTree T;
static Node *root;
while (1)
{
std::cout<<"AVL Tree Implementation"<<std::endl;
std::cout<<"1.Insert Element into the tree"<<std::endl;
std::cout<<"2.InOrder traversal"<<std::endl;
std::cout<<"3.Exit"<<std::endl;
std::cout<<"Enter your Choice: ";
std::cin>>Choice;
switch(Choice)
{
case 1:
std::cout<<"Enter value to be inserted: ";
std::cin>>Key;
root = T.insertToAVL(root,Key);
break;
case 2:
if (root == nullptr)
{
std::cout<<"Tree is Empty"<<std::endl;
continue;
}
std::cout<<"Inorder Traversal:"<<std::endl;
T.InOrder(root);
std::cout<<std::endl;
break;
case 3:
std::exit(1);
break;
default:
std::cout<<"Wrong Choice"<<std::endl;
}
}
return 0;
}
Applications
Applications of AVL Tree are as follows:
-
AVL trees are used for scenario that requires frequent insertion and search.
-
Used in Memory management subsystem of linux kernel to search memory regions of processes during preemption.
-
Situations which require fast searching
