
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article at OpenGenus, we will solve the problem called Minimum Absolute Difference Between Elements With Constraint. The article will guide you through the intuition of how to solve the problem using the concept of Binary Search and Ordered Set which is frequently asked in coding interviews of various tech companies.
Table of contents:
- Problem Statement
- Twist in Problem
- Intiution behind using Binary Search and Ordered Set
- Implementing the Solution
- Time and Space Complexity
1. Problem Statement
The problem statement is very straight forward which states :
Given a 0-indexed integer array nums and an integer x, determine the smallest absolute difference between two elements in the array that have a distance of at least x indices. In simpler terms, identify two indices i and j such that abs(i - j) >= x, and minimize abs(nums[i] - nums[j]). Provide an integer representing the minimum absolute difference between two elements separated by at least x indices.
Input: nums = [4,3,2,4], x = 2
Output: 0
Explanation : We can select nums[0] = 4 and nums[3] = 4.
They are at least 2 indices apart, and their absolute difference is the minimum, 0. It can be shown that 0 is the optimal answer.
The only constraint in the problem is to find two indices i and j with minimum absolute difference abs(i - j) >= x, which implies that i and j should be x distance apart. Now we have indices from 0 to 3 where x = 2 then ,
- For
i = 0, we have possiblej = 2 , 3. - For
i = 1, we have possiblej = 3. - For
i = 2, we have noj. - For
i = 3, we have noj.
Therefore , we have to find the minimum absoulate difference in between the values of pairs of above indices.
Suppose values are : nums = [4,3,2,4] and x = 2 as above then ,
-
For
i = 0: Pairs are ( 0 , 2 ) = 2 , ( 0 , 3 ) = 0. -
For
i = 1: Pairs are ( 1 , 3 ) = 1. -
For
i = 2: No pairs. -
For
i = 3: No pairs.
Therefore , minimum absolute difference is 0.
2. Twist in Problem
The above example can we easily solved without as difficulty using the simple loops in n^2 time complexity.
class Solution {
public:
int minAbsoluteDifference(vector<int>& nums, int x) {
int mini = INT_MAX;
for(int i = 0 ; i < nums.size(); i++){
for(int j = i + x ; j < nums.size(); j++){
mini = min(mini , abs(nums[i] - nums[j]));
}
}
return mini;
}
};
But the twist is problem have constraints of :
1 <= nums.length <= 10^51 <= nums[i] <= 10^90 <= x < nums.length
For n^2 complexity it will execute in (10^5)^2 which is 10^10 iterations , which are too much in complexity and can't be executed in 1 sec on the tester. Therefore , we need to decrease the complexity to either O(nlogn) or O(n) time complexity.
3. Intiution behind using Binary Search and Ordered Set
The problem can be solved in O(nlogn) with the use of binary search and ordered set. Let' frame the proble more correctly in terms of a sliding window as shown in image below :
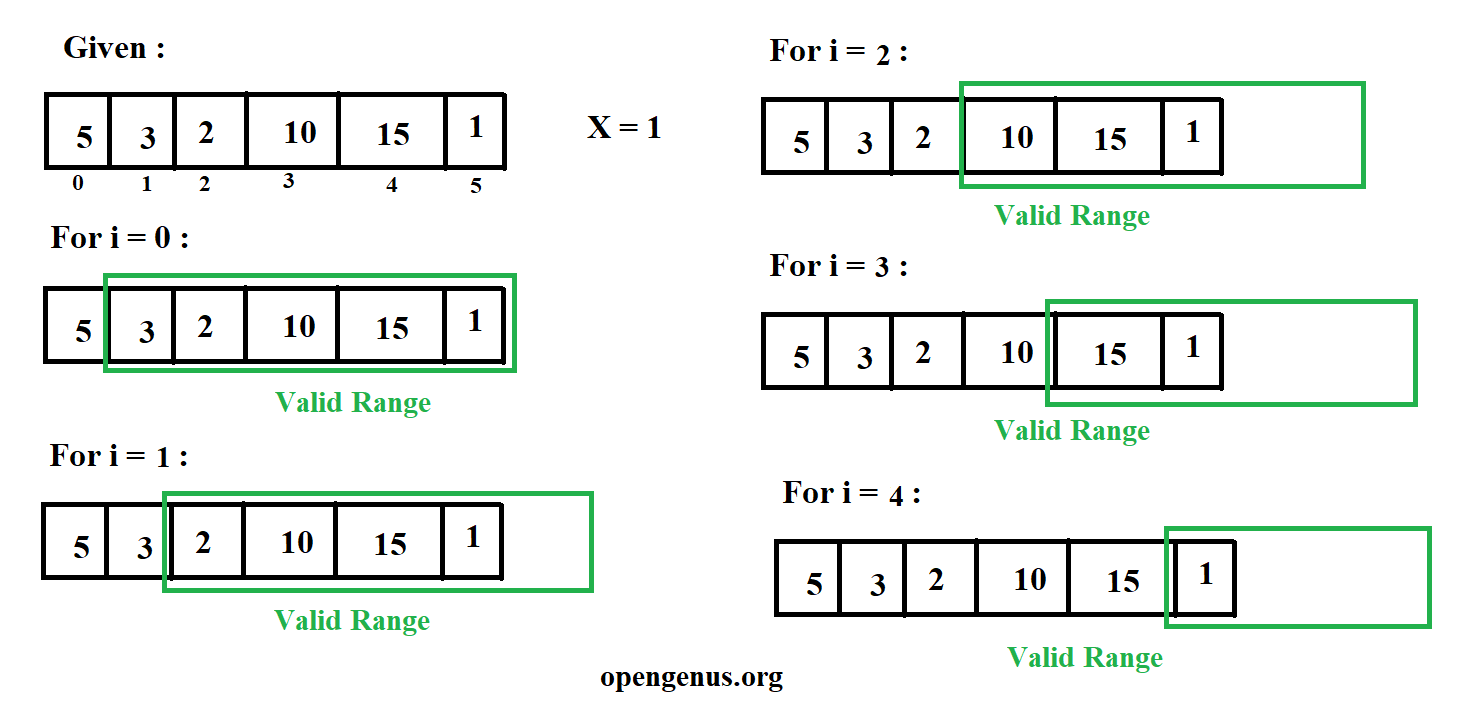
Theoratically we have :
nums = [5,3,2,10,15,1] , x = 1 , index = 0 to 5
For i = 0 : valid are j = [1,2,3,4,5]
For i = 1 : valid are j = [2,3,4,5]
For i = 2 : valid are j = [3,4,5]
For i = 3 : valid are j = [4,5]
For i = 4 : valid are j = [5]
For i = 5 : valid are j = []
Therefore , to solve this for each i we need to find the element closet to the nums[i] for all jor we can say min( abs (nums[j] - nums[i] ) ) for each possible j.
The solution to above problem to find the minimum absolute difference in fastest way to find closest is using binary search which needs elements sorted which means for nums[i] we need to find the nums[j] which is min( abs (nums[j] - nums[i] ) ) among all possible j values.
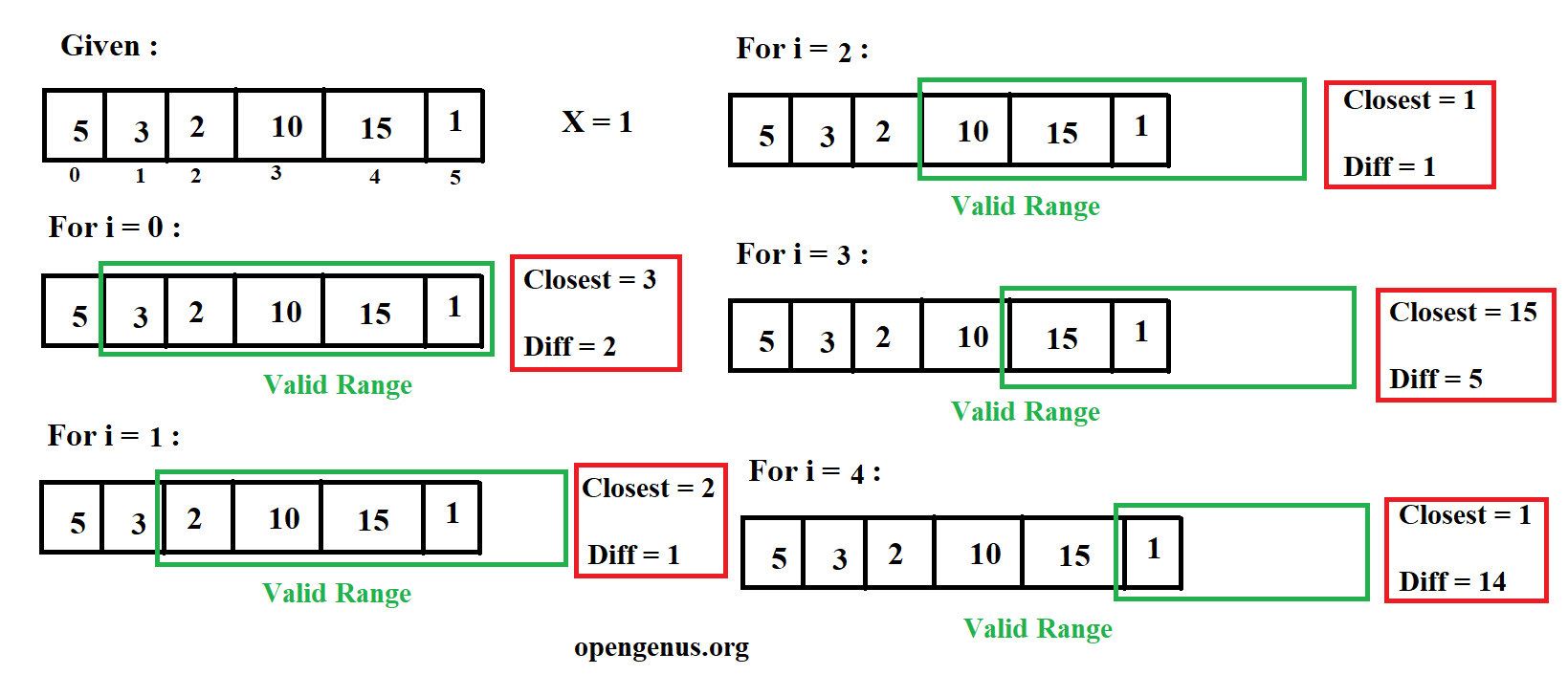
But what's stopping us to implement above problem ?
Todo the above task we need to see the ahead for each index. Therefore , Issue : To do so , for each i we need to consieder all the elements ahead of i + x, consider if x = 3 for above problem,
nums = [5,3,2,10,15,1], x = 3 , index = 0 to 5
For i = 0 : valid are j = [3,4,5]
For i = 1 : valid are j = [4,5]
For i = 2 : valid are j = [5]
For i = 3 : valid are j = []
For i = 4 : valid are j = []
For i = 5 : valid are j = []
So to implement the above we can do as follow by maintaining a sorted vector :
class Solution {
public:
int minAbsoluteDifference(vector<int>& nums, int x) {
int i = 0 , j = x;
vector<int> sorted;
for(int k = j ; k < nums.size(); k++){
sorted.push_back(nums[k]);
}
sort(sorted.begin() , sorted.end());
int ans = INT_MAX;
while(!sorted.empty()){
// find closest element to nums[i]
auto it = lower_bound(sorted.begin() , sorted.end() , nums[i]);
// check if iterator is not at the end of vector
if(it != sorted.end()){
ans = min(ans , abs(nums[i] - (*it)));
}
// considering one value less as lower bound may be pointing tovalue greater than nums[i]
if(it != sorted.begin()){
--it;
ans = min(ans , abs(nums[i] - (*it)));
}
// remove the nums[j] from sorted as it's not valid anymore
auto todel = find(sorted.begin() , sorted.end() , nums[j]);
if(todel != sorted.end()){
sorted.erase(todel);
}
i++;
j++;
}
return ans;
}
};
Input:
nums = [5,3,2,10,15] , x = 3
Output :
5
In above code we add the elements which we need to see ahead. We need them sorted so we sort them only once. We keep on removing the elements as j move ahead. We use the lower_bound function to find the closest element which use binary search in background. The above code solves the problem in O(nlogn) time.
Time Complexity:
Let's denote n as the size of the input vector nums. The main part of the algorithm is the while loop. Inside the loop, the operations are mostly constant time, except for the lower_bound , find and erase operations.
Let's analyze the complexity of each part:
The loop runs n - x times, where n is the size of nums. This is because the loop iterates from x to n - 1. Inside the loop, lower_bound, find and erase both take logarithmic time complexity (O(log m)), where m is the size of the sorted vector. Therefore, the overall time complexity of the provided code is roughly O((n - x) * log(m)), where n is the size of the input vector nums and m is the size of the sorted vector.
Space Complexity:
The space complexity is O(m) where m is the sorted vector.
As we solved the problem but is it the best solution ? No , we can still improve the implementation by using the ordered set. The ordered set can be used in place of the sorted vector. Ordered set can be used to keep the sorted data but in that way the implementation becomes difficult as ordered set only stores an element once so we need to maintain a map in order to keep track of the count of each element and check it before removing. So to fulfill the following the implementation below can be used :
class Solution {
public:
unordered_map<int, int> repeat;
int minAbsoluteDifference(vector<int>& nums, int x) {
return solve1(nums, x);
}
int solve1(vector<int>& nums, int x) {
set<int> s;
// adding elements after x into set
for (int i = x; i < nums.size(); i++) {
repeat[nums[i]]++;
s.insert(nums[i]);
}
int ans = INT_MAX;
// looping to all elements
for (int i = 0; i < nums.size(); i++) {
if (s.empty()) {
break;
}
// cout<<" for i = "<<i<<" set = ";
// printSet(s);
// finding cloest element
auto it = s.lower_bound(nums[i]);
// checking if iterator is not end of set
if (it != s.end()) {
ans = min(ans, abs(nums[i] - (*it)));
}
// considering one value less as lower bound may be pointing tovalue
// greater than nums[i]
if (it != s.begin()) {
--it;
ans = min(ans, abs(nums[i] - (*it)));
}
// remove the element i+x as it was only to be considered for i not
// valid for i+x
if (i + x <= nums.size() - 1) {
// handling if repeated elements example [19 , 14 , 14]
if (repeat[nums[i + x]] > 1) {
// dnot remove if element is repeated as it will be used
// again
repeat[nums[i + x]]--;
continue;
}
s.erase(nums[i + x]);
}
}
return ans;
}
};
Time Complexity: O((n - x) * log(min(n, n - x))).
Space Complexity: O(min(n, n - x) + n).
4. Implementing the Solution
Above implementation is good in terms of time and space complexity. The problem can be formulated in reverse also. But why ? To avoid the use of map which creates overhead of space and time to check the count of each element. Therefore we formulate our solution in reverse order.
nums = [5,3,2,10,15,1], x = 3 , index = 0 to 5
For each element we will check if it can use any previous index:
For i = 0 : can't use any previous
For i = 1 : can't use any previous
For i = 2 : can't use any previous
For i = 3 : can use 0 so set = [0]
For i = 4 : can use 1 and 0 so set = [0 , 1]
For i = 5 : can use 2,1,and 0 so set = [0 , 1 , 2]
We have revsersed the problem by find suitable i instead of j in expression min( abs (nums[j] - nums[i] ) ). So we dont need to keep track of count of each element as we are adding element to set only when required and it doesn't need to be removed later as the j will increase the possibilities of i keeps on increasing. The code is as follows :
class Solution {
public:
int minAbsoluteDifference(vector<int>& nums, int x) {
set<int> s;
int ans = INT_MAX;
for(int i = 0; i < nums.size() ; i++){
// adding the required element only
if(i >= x){
s.insert(nums[i-x]);
}
// finding cloest element
auto it = s.lower_bound(nums[i]);
// checking if iterator is not end of set
if(it != s.end()){
ans = min(ans , abs(nums[i] - (*it)));
}
// considering one value less as lower bound may be pointing tovalue greater than i
if(it != s.begin()){
--it;
ans = min(ans , abs(nums[i] - (*it)));
}
}
return ans;
}
};
Input :
nums = [5,3,2,10,15] , x = 3
Output :
5
Here's a step-by-step explanation:
- Initialize an empty set
sto keep track of the elements that are at mostxpositions away from the current element. - Initialize a variable
ansto store the minimum absolute difference. SetanstoINT_MAXinitially. - Iterate through each element
nums[i]in the input vector:- If
iis greater than or equal tox, insert the element at positioni - xinto the sets. This step ensures that the set only contains elements within the desired range. - Find the closest element to
nums[i]in the setsusinglower_bound. - If the iterator is not at the end of the set, update
answith the minimum absolute difference betweennums[i]and the found element. - Consider one value less than the lower bound, as it may be pointing to a value greater than
nums[i]. Updateansaccordingly.
- If
- After iterating through all elements,
answill contain the minimum absolute difference.
5. Time and Space Complexity
The analysis of space and time complexity is as follows :
1. Time Complexity:
The time complexity of this solution is O(n * log(x)), where n is the size of the input vector nums. The primary factor contributing to the time complexity is the logarithmic time complexity of the lower_bound operation in the set.
2. Space Complexity:
The space complexity is O(x), where x is the maximum allowed distance between elements. This is due to the size of the set s, which can contain at most x elements.
Key Takeaways (Minimum Absolute Difference Between Elements With Constraint)
- The article tackles the "Minimum Absolute Difference Between Elements With Constraint" problem using binary search and ordered set, common in coding interviews.
- The optimized solution achieves O(n * log(x)) time complexity by efficiently finding the closest element within a specified range.
- An alternative implementation in reverse order simplifies the code, avoids the need for a map, and maintains a space complexity of O(x).
- The C++ solution demonstrates a practical application of binary search and set manipulation, showcasing a balance between time and space efficiency.
