In this article at OpenGenus, we will solve the problem of getting maximum profit by buying and selling a share at most k times. The article will guide you through the intuition of how to solve the problem using the concept of backtracking and dynamic programming which is frequently asked in coding interviews of various tech companies.

Table of contents:

1. Problem Statement
2. Intuition behind using Backtracking
3. Why need Dynamic Programming ?
4. Implementing the Solution
5. Time and Space Complexity

1. Problem Statement

You are given an integer array prices where prices[i] is the price of a given stock on the ith day, and an integer k.

Find the maximum profit you can achieve. You may complete at most k transactions: i.e. you may buy at most k times and sell at most k times.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Let's understand the problem with an example :

Suppose we are given the k = 2, prices = [3 ,2 ,6 ,5 ,0 ,3 ] , which means we can make at most 2 transactions and we have to generate the maximum profit in at most 2 transactions not more than that, which implies that we can buy and sell at most 2 times.So for instance I can buy on day 1 and sell on day 4 which completes one transaction and for second transaction we can buy on day 5 and sell on day 7. Also there is a condition that we have to sell the stock first and then buy again which means if I buy on day 1 then I can not buy again until I sell it. So for the above problem we have following cases :

1. Buy on Day 1 :

   Buy on Day 1 with a price of 3 and now we want to sell the stock for some profit. Therefore as we can see the prices list one of the choice to sell the Day 3 or Day 4 with some profit or make zero profit on Day 6. Let's explore the choices one by one :

   1.1. Sell on Day 3 : Sell on day 3 make profit of 6-3 = 3.

   • 1.1.1. Now choose next day to buy as we can make 1 more transaction as value of k was 2. The k is now 1. So we can either make profit of 3 and stop here or continue to make one more transaction.
   • 1.1.2. Let's see the choice of next Buy day which are : day 4 , day 5 , day 6. So if we buy on day 4 , at price 5 then we can't sell it profitably on day 5 and day 6. So, let's explore the next choice of buying at day 5 at price 0 and sell on day 6, therefore profit is 3 - 0 = 3. Therefore profit = 3 + 3 = 6 total.

   1.2. Sell on Day 4 : Sell on day 4 with profit of 5-3 = 2.

   • 1.2.1 Now choose next day to buy as we can make 1 more transaction as value of k was 3. The k is now 1. So we can either make profit of 2 and stop here or continue to make one more transaction.
   • 1.2.2. Let's see the choice of next Buy day which are : day 5 , day 6. So if we buy on day 5 , at price 0 and sell on day 6, therefore profit is 3 - 0 = 3. Therefore profit = 2 + 3 = 5 total.

   1.3. Sell on Day 6 : We make a profit 0, and we stop here as there no more days left.

2. Buy on Day 2 : The above same process goes and we keep track of maximum profit.
   .
   .
   .
   .

3. Buy on Day 6 : The above same process goes and we keep track of maximum profit.

2. Intuition behind using Backtracking

Suppose we are given the k = 2, prices = [3 ,2 ,6 ,5 ,0 ,3 ] ,
which means that we are given the prices of the share at different point of times and we can buy and sell only 2 times.

One of the possible solution for the above example is :

1. We can buy the buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4.
2. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

Here we are making choices where we choose to buy on ith day and sell on jth day with a profit p and we can do this process at most 'k' times. This will lead us to a dependency tree of choices. We may need to backtrack both buy and sell choices. The figure below shows the tree if we choose the day 1 as buy choice.

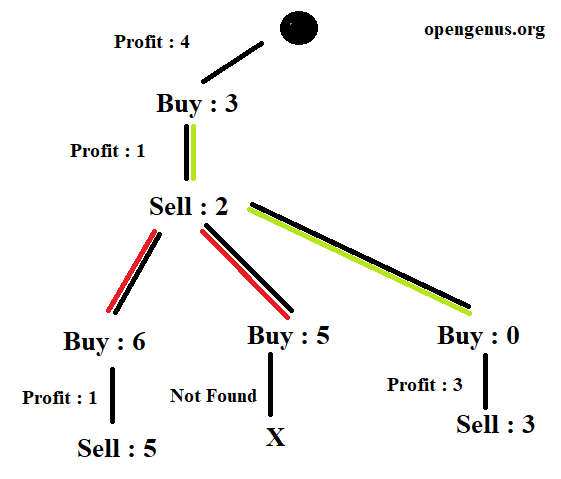
The green edge is the maximum profit edge. We backtrack the first two edges which are highlighted in red and take the maximum out of the three edges. Therefore the maximum profit if we buy on day 1 at price 3 and sell on day 2 with price 2 we get a profit of 4. Similar tree will grow for the sell at day 3 and so. But note that the tree will only grow upto 2 levels only as k = 2.The code using backtracking is as follows :

class Solution {
public:
    
    // driver function 
    int maxProfit(int k, vector<int>& prices) {
          
        // passing index , k , prices
        return solve(0, k, prices);
    }
    
    int solve(int index, int k, vector<int>& prices) {
           
        // if we have k transactions we can stop
        if (k == 0) {
            return 0;
        }
        // if we have seen all the days we can stop
        if (index >= prices.size()) {
            return 0;
        }
        
        // We need to find the maximum profit by either skipping the current day
        // (i.e., not making any transaction on this day) or making a transaction
        // on this day and then finding the maximum profit for the remaining days.
        
        // skipping the current day and keeping the k same as no transaction is made
        int maxProfitWithoutTransaction = solve(index + 1, k, prices);
        
        // if we make the transaction on the index day what will be the maximum profit
        int maxProfitWithTransaction = 0;
        
        // if index is the day of buying we are finding the ith day on which we can sell and calucate profit for next k-1 transactions starting from i+1
        for (int i = index + 1; i < prices.size(); i++) {
        
            int profit = prices[i] - prices[index];
            if (profit >= 0) {
                int nextProfit = solve(i + 1, k - 1, prices);
                maxProfitWithTransaction = max(maxProfitWithTransaction, profit + nextProfit);
                
            }
        }

        return max(maxProfitWithoutTransaction, maxProfitWithTransaction);
    }
};

The given code is a C++ implementation of a solution to find the maximum profit that can be obtained from at most k transactions in a stock market. The stock prices are given as an array prices, where prices[i] represents the price of the stock on the ith day.

The solution uses a recursive approach to explore all possible transactions and find the maximum profit. The maxProfit function serves as a driver function, and it initializes the recursive process by calling the solve function with initial parameters.

The solve function takes three parameters:

1. index: The current index or day in the prices array.
2. k: The remaining number of transactions allowed.
3. prices: The array of stock prices.

The base cases are checked first:

• If k becomes 0 (no more transactions allowed), the function returns 0.
• If the index goes beyond the size of the prices array, meaning all days have been considered, the function returns 0.

The main logic involves finding the maximum profit by either skipping the current day (no transaction) or making a transaction on the current day and finding the maximum profit for the remaining days. The maximum profit without the current transaction is calculated by recursively calling the function with the next index and the same k. The maximum profit with the current transaction involves iterating over the remaining days, calculating the profit if a transaction is made on the current day, and recursively finding the maximum profit for the remaining transactions.

The line maxProfitWithTransaction = max(maxProfitWithTransaction, profit + nextProfit); updates the maximum profit with the current transaction if the calculated profit on the current day is greater than the current maximum.

The function returns the maximum profit among the two cases: with and without the current transaction.

Complexity Analysis :

The time and space complexity as follows :

1.Time Complexity: The time complexity of the code is exponential, specifically O(2^n), where 'n' is the number of days (size of the input vector prices). This is because the code explores all possible combinations of making transactions or not making transactions on each day, and the recursive calls lead to an exponential number of function calls.

2. Size Complexity : The space complexity is determined by the depth of the recursion, which is influenced by the number of transactions 'k'. In the worst case, the recursion depth can be 'k', as the algorithm explores k transactions.

It's worth noting that this solution has exponential time complexity, as it explores all possible combinations of transactions. For large inputs, it may be inefficient, and dynamic programming techniques like memoization or tabulation could be applied to optimize the solution.

3. Why need Dynamic Programming ?

Since the tree may grow too much with different branches and branches may get reused. So we need the dynamic programming to cache the results from different branches. We will need a two dimensional grid to do so. As the one dimension will be used to keep track of each day and the second dimension will be used to keep track of the k which means that how many choices more we can make at the current day.

Therefore the code in backtracking optimized with the dynamic programming is as follows :

class Solution {
public:

    // 2D Dynamic Programming dp[index][k]
    vector<vector<int>> dp;
    
    // driver function 
    int maxProfit(int k, vector<int>& prices) {
          
        int n = prices.size();
        dp.resize(n, vector<int>(k+1 , -1));
        // passing index , k , prices
        return solve(0, k, prices);
    }
    
    int solve(int index, int k, vector<int>& prices) {
           
        // if we have k transactions we can stop
        if (k == 0) {
            return 0;
        }
        // if we have seen all the days we can stop
        if (index >= prices.size()) {
            return 0;
        }
        // if we have cached result means we have seen the branch we reuse it
        if (dp[index][k] != -1) {
            return dp[index][k];
        }
        
        // We need to find the maximum profit by either skipping the current day
        // (i.e., not making any transaction on this day) or making a transaction
        // on this day and then finding the maximum profit for the remaining days.
        
        // skipping the current day and keeping the k same as no transaction is made
        int maxProfitWithoutTransaction = solve(index + 1, k, prices);
        
        // if we make the transaction on the index day what will be the maximum profit
        int maxProfitWithTransaction = 0;
        
        // if index is the day of buying we are finding the ith day on which we can sell and calucate profit for next k-1 transactions starting from i+1
        for (int i = index + 1; i < prices.size(); i++) {
        
            int profit = prices[i] - prices[index];
            if (profit >= 0) {
                int nextProfit = solve(i + 1, k - 1, prices);
                maxProfitWithTransaction = max(maxProfitWithTransaction, profit + nextProfit);
                
            }
        }
        
        // caching the results into the dp
        dp[index][k] = max(maxProfitWithoutTransaction, maxProfitWithTransaction);
        return dp[index][k];
    }
};

This solution is a dynamic programming (DP) approach to solving the problem of finding the maximum profit that can be obtained from at most k transactions in a stock market, where stock prices are given as an array prices. The DP approach uses memoization to store the results of subproblems in a 2D array dp to avoid redundant calculations and improve efficiency.

4. Implementing the Solution

Therefore the complete implementation of the solution can be seen below where the Solution class is same as the dynamic programming and the added main function. The main function includes the call to maxProfit function.

#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
    // 2D Dynamic Programming dp[index][k]
    vector<vector<int>> dp;

    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        
        // Initialize the memoization table with -1 (unvisited) values
        dp.resize(n, vector<int>(k + 1, -1));
        
        // Call the recursive solve function to find the maximum profit
        return solve(0, k, prices);
    }

    int solve(int index, int k, vector<int>& prices) {
        // Base case: if no more transactions are allowed or all days are considered
        if (k == 0 || index >= prices.size()) {
            return 0;
        }

        // If the result for this subproblem is already calculated, return it
        if (dp[index][k] != -1) {
            return dp[index][k];
        }

        // We need to find the maximum profit by either skipping the current day
        // (i.e., not making any transaction on this day) or making a transaction
        // on this day and then finding the maximum profit for the remaining days.

        // Calculate the maximum profit without making a transaction on the current day
        int maxProfitWithoutTransaction = solve(index + 1, k, prices);

        // Calculate the maximum profit with making a transaction on the current day
        int maxProfitWithTransaction = 0;
        
        // If index is the day of buying, find the day on which we can sell
        for (int i = index + 1; i < prices.size(); i++) {
            int profit = prices[i] - prices[index];
            
            // Ensure a valid profit before considering it
            if (profit >= 0) {
                // Calculate the profit for the remaining transactions starting from i+1
                int nextProfit = solve(i + 1, k - 1, prices);
                // Update the maximum profit with the current transaction
                maxProfitWithTransaction = max(maxProfitWithTransaction, profit + nextProfit);
            }
        }

        // Cache the results into the dp table
        dp[index][k] = max(maxProfitWithoutTransaction, maxProfitWithTransaction);
        
        // Return the maximum profit for the current state
        return dp[index][k];
    }
};

int main() {
    Solution solution;

    // Example usage:
    vector<int> prices = {3, 2, 6, 5, 0, 3};
    int k = 2;

    // Call the maxProfit method and print the result
    int maxProfit = solution.maxProfit(k, prices);

    cout << "Maximum Profit: " << maxProfit << endl;

    return 0;
}

Output :

Maximum Profit: 7

5. Time and Space Complexity

Let's analyze the time and space complexity of the provided solution:

1. Time Complexity:

   The time complexity of the solution is determined by the number of unique subproblems that need to be solved. Since the solution uses memoization to avoid redundant calculations, the time complexity is greatly reduced.

   The time complexity is O(n * k), where:

   • n is the number of days (length of the prices array).
   • k is the maximum number of transactions allowed.

   This is because, for each combination of index and k, the solution explores the possibilities of making or not making a transaction on a particular day. There are at most n * k unique subproblems, and each subproblem takes constant time to solve once it's memoized.

2. Space Complexity:

   The space complexity is influenced by the memoization table (dp) and the recursive call stack.

   • Memoization Table (dp):

     • The memoization table has dimensions n x (k + 1).
     • The space complexity due to the memoization table is O(n * k).

   • Recursive Call Stack:

     • The maximum depth of the recursive call stack is k.
     • The space complexity due to the recursive call stack is O(k).

   Combining both components, the overall space complexity is O(n * k) + O(k), which simplifies to O(n * k).

In summary, the provided solution is a dynamic programming solution with memoization, resulting in a time complexity of O(n * k) and a space complexity of O(n * k). The time complexity is significantly improved compared to a naive recursive solution without memoization.