
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have covered the Backtracking Algorithm for Sudoku and compared with the Brute Force approach. We have presented the Time and Space Complexity for various cases.
| Table of Contents |
|---|
| 1) Introduction |
| 2) Naive Approach |
| 3) Backtracking |
| 4) Time and Space Complexity |
| 5) Conclusion |
1)Introduction
Probably you might know what sudoku is or might have heard somewhere about it.Let's begin with a brief note on it.
Sudoku is a logic based number placement puzzle.
Given a 9×9 grid, with some initial values filled.The objective is to fill all the empty cells of the grid with numbers such that it becomes valid.
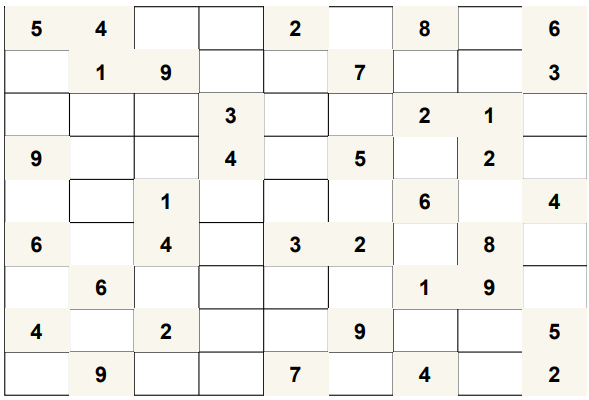
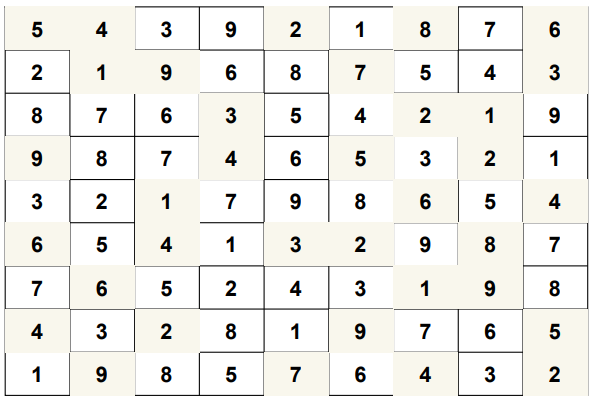
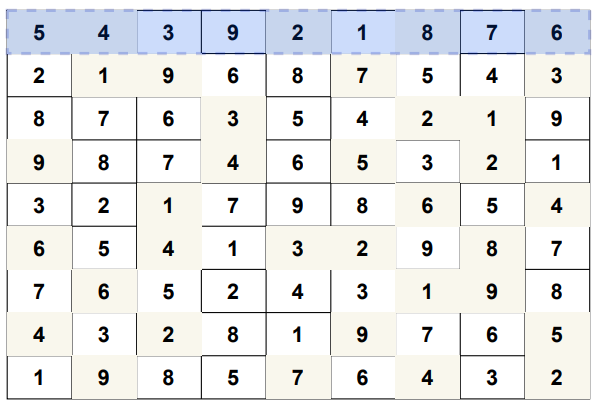
A sudoku is valid if it satisfies all the following properties:
1.Each row contains unique values ranging from 1 to 9.
2.Each column contains unique values ranging from 1 to 9.
3.Each of 9 sub-squares ,of size 3×3, contains unique values from 1 to 9.
2)Naive Approach
In naive approach,the algorithm fills in the empty cells without any logic and later checks whether it was a valid placement.
This can be much time consuming and highly inefficient. A slight optimization to this would be the backtracking approach.
3)Backtracking
Backtracking is a kind of brute-force approach which comes into picture when solving a problem requires considering multiple choices as we don't know which choice is correct and we try to solve the problem using trail and error method considering one choice at a time until required answer is obtained.
Sudoku can be solved in the way mentioned above.
The difference between brute-force and backtracking is that in backtracking, we do not explore all the possible options instead we explore only worthy options and build the solution incrementally.
"This algorithm visits all the empty cells in some order,filling the digits incrementally, backtracks when a number is not found to be valid.The program starts by filling '1' in the first cell if there are no violations, then advances to the second cell and places '1' incase violation occurs then increments and places '2'.It checks incrementally in this way and when none of the '1' to '9' numbers fit in this cell then the algorithm leaves the cell blank and goes back to the previous cell.The value in that cell is incremented and this process continues until all the cells are filled."
STEPS:
-We start by finding an unfilled cell(i,j).
-If all the cells are filled then a valid sudoku is obtained.
-We try to place every number between 1 to 9 in the unfilled cell.
-Before placing we check for the constraints by checking the current row,current column and current 3×3 submatrix.
-If any of the any of the constraint becomes false we'll not place that number at (i,j).
-If all the constraints are true then we'll place that number at (i,j) and then repeat the process by finding an unfilled cell.
-If at any point none of the numbers can be placed at (i,j) then we've to backtrack and change the values for already visited cells
To check the 3×3 submatrix(box) condition
Find the center cell using the following
r=(row//3)×3+1 c=(col//3)×3+1
For example take (5,6),
r=(5//3)×3+1=1×3+1=3+1=4
c=(6//3)×3+1=2×3+1=6+1=7
Hence the center cell for box containing (5,6) is (4,7)
After finding the center cell it easy to check as all the values in the box will be at unit distance from the center cell.
Let's look at the algorithm.
PSEUDOCODE:
solve(grid)
if(no more cells are there to explore)
return true;
for(all available choices)
try one choice c;
if(solve(grid with choice c made) is true)
return true;
unmake choice c;
return false;
ALGORITHM:
sudokuSolver(grid)
1.Find an unfilled cell
(i,j)ingrid
2.If all the cells are filled then
2.1. A valid sudoku is obtained hencereturn true
3.For eachnumin 1 to 9
3.1. If the cell(i,j)can be filled withnumthen fill it withnumtemporarily to check
3.2. If sudokuSolver(grid) istruethenreturn true
3.3. If the cell(i,j)can't be filled withnumthe mark it as unfilled to trigger backtracking
4.If none of the numbers from 1 to 9 can be filled in cell(i,j)thenreturn falseas there is no solution for this sudoku
Implementation
# function to print grid
def printGrid(grid):
for x in grid:
for y in x:
print(y,end=" ")
print()
# function to check if the value to be assigned to a cell already exists in that row of that cell
# it returns true if 'val' can be placed in a cell with row number as 'row'
def rowCheck(grid,row,val):
#iterate through that row
for j in range(9):
# if value to be assigned is found then
# it can't be placed in that cell
if val==grid[row][j]:
return False
return True
# function to check if the value to be assigned to a cell already exists in that column of that cell
# it returns true if 'val' can be placed in a cell with column number as 'col'
def colCheck(grid,col,val):
#iterate through that column
for i in range(9):
# if value to be assigned is found then
# it can't be placed in that cell
if val==grid[i][col]:
return False
return True
#function to check "box" condition
def boxCheck(grid,row,col,val):
# get the center cell(r,c) of the box
# with simple formula below
r=(row//3)*3+1
c=(col//3)*3+1
# iterate through each cell of the box
for i in [-1,0,1]:
for j in [-1,0,1]:
# for each cell of the box check if the value to be placed exists
# if exits then it can't be placed in that cell
if grid[r+i][c+j]==val:
return False
return True
# function to find unassigned cell(a cell which doesn't contain a value) in the grid
def findUnassigned(grid):
for i in range(9):
for j in range(9):
# cell which contains dot(.) is unassigned
if grid[i][j]==".":
return i,j
# if no cell left unassigned
return -1,-1
# function to complete the sudoku
def sudokuSolver(grid):
# find an unassigned cell in the grid
i,j=findUnassigned(grid)
# if no cell remain unassigned then the grid is filled completely and is valid
if i==-1 and j==-1:
return True
# for each 'num' ranging from 1 to 9 check if it can be placed at '(i,j)'
for num in ["1","2","3","4","5","6","7","8","9"]:
# 'num' can be placed at '(i,j)' if
# any value in row 'i' is not equal to 'num'
# any value in column 'j' is not equal to 'num'
# any value in the box it belongs to is not equal to 'num'
if rowCheck(grid,i,num) and colCheck(grid,j,num) and boxCheck(grid,i,j,num):
#all the conditions are satisfied
#place 'num' at '(i,j)' temporarily
grid[i][j]=num
#check for the next cells
if sudokuSolver(grid):
return True
# we've reached here because the choice we made by putting some 'num' here was wrong
# hence now leave the cell unassigned to try another possibilities
grid[i][j]="."
# putting any value doesn't solve the grid that means we've made a wrong choice earlier
# if no value can be placed at '(i,j)' then returns false meaning that the current
# sudoku is not feasible and try for another possibilities
return False
grid=[
[".","8",".","5","3",".","2","7","6"],
[".","5",".","6",".",".",".",".","."],
["6","1","3",".",".",".",".",".","."],
[".",".","6",".","5",".",".",".","."],
[".","3","2",".",".",".","7",".","1"],
["7","4","5",".",".","8","6","9","3"],
[".","7",".","9","6",".","5",".","."],
["4",".",".","1","8",".",".","6","7"],
["5",".",".",".",".","4","8","2","9"]
]
if sudokuSolver(grid):
printGrid(grid)
else:
print("No solution exists!")
9 8 4 5 3 1 2 7 6
2 5 7 6 4 9 1 3 8
6 1 3 8 2 7 9 4 5
1 9 6 7 5 3 4 8 2
8 3 2 4 9 6 7 5 1
7 4 5 2 1 8 6 9 3
3 7 8 9 6 2 5 1 4
4 2 9 1 8 5 3 6 7
5 6 1 3 7 4 8 2 9
4)Time and Space Complexity
Consider there are m unfilled cells in the sudoku
Time Complexity:
The backtracking algorithm takes O(9m) time complexity in the worst case since for every unfilled cell there are 9 possibilites to explore and there are m unfilled cells in the sudoku.
- Worst Case Time Complexity: O(9m)
- Average Case Time Complexity: O(9m)
- Best Case Time Complexity: O(m2) [This takes place when the number of backtracking steps are minimized]
For Brute force approach:
- Worst Case Time Complexity: O(9m)
- Average Case Time Complexity: O(9m)
- Best Case Time Complexity: O(m)
Note, in the best case, Brute force approach performs better than Backtracking approach. Despite same Time Complexity for average and worst case, the exact number of steps in Backtracking approach is much less and hence, is an efficient approach to solve Sudoku.
Space Complexity:
At most, there can be m function calls in the recursion stack. Hence the space complexity would be O(m).
5) Conclusion
Other ways to solve sudoku are:
- Crook’s algorithm
- Constraint programming
- AI based approach
With this article at OpenGenus, you must have the complete idea of Backtracking Algorithm for Sudoku.
