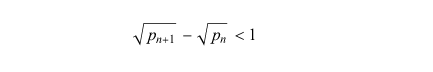Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Table of contents
- Definitions
- Algorithm
- Time complexity
- A way of implementation
1. Definitions
A conjecture is synonymous with hypothesis and consists in having no proof yet to be verified as true of false. It starts from a real fact and it has a rule for it.
A prime number is a number that is only divisible to 1 and itself.
The first few primes are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …
Notice that 1 is not part of this series.
There is no mathematician who has not been looking at this unique series of numbers and tried to find a relation of 2 consecutive prime numbers.
We can first try to make a difference of them and check how the gap between them evolves and we can notice that except for the first 2 primes where the gap is 1 which is an odd number, the rest of the gaps are all even numbers.
Ex for the first 60 prime gaps:
1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2
Do you find a pattern here ?
I've tried to find one, for example the repetition of the 4,2,4 subset, but the more series grow the more repetion diminishing and bigger even numbers start to show up.
But that doesn't help too much as we cannot predict a n-th prime number based on its predecesors, as in the factorial or Fibonacci series.
Notice that except for the the first gap, all the others are even numbers.
Andrica's conjecture states that for every gap between two consecutive square roots of prime numbers, the value of it is less than 1.
2. Algorithm
Since the Andrica's conjecture is a formula that is using the prime numbers, the only thing that we need to implement is to generate the prime numbers series.
If you are a beginner in programming if you want to check if a number is prime you might want to use a simple loop to check for all numbers between 2 and the square root of it !
loop
i <- 2..sqrt(n)
if (n mod i == 0) return false
end loop
return true
This check might be time consumming and double checking. Why ? because you start checking from number 2 and continue until you reach the square root number. But in this subset there might be other numbers that are divided with other prime numbers so there is no need to check for them again !
To avoid this situation we can use an array to store the previous checked prime numbers, i.e. we only divide the given number to the prime numbers before it, this method is called memoaization.
procedure isPrime(array p, n)
i <- 0
while p[i] <= sqrt(n)
if (n mod p[i] == 0) return false
return true
procedure generatePrime(n)
array p
j <- 0
for i <- 3..n-1
if (isPrime(p, i))
{
p[j] <- i
j <- j + 1
}
Another way is to use the sieve of Eratosthenes , the sieve of Sundaram or the sieve of Atkin
3. Time complexity
Since we check all the numbers the generatePrime function will be O(N).
For the isPrime function we check only for the prime numbers before the square root of N, which depends on the size of the subset of the prime numbers which means usually O(log N)
So, generating the prime series will be O(N logN)
4. A way of implementation
#include <iostream>
#include <math.h>
using namespace std;
bool isPrime(int *p, int n)
{
int sqrtn = sqrt(n), i=0;
while ( p[i] <= sqrtn )
if(n%p[i++] == 0) return false;
return true;
}
int & generatePrime(int n, int &size)
{
int *p, i, j;
p = new int[n];
j=0;
p[j++]=2;
for (i=3; i < n; i++)
if(isPrime(p, i)) p[j++] = i;
size = j;
return *p;
}
void checkAndricaConjecture(int n)
{
int i=0, size;
int *p = &generatePrime(n,size);
while (i < size-2)
cout <<p[i]<<" "<< sqrt(p[i+1]) - sqrt(p[i]) << endl,i++;
}
int main()
{
int n = 500;
checkAndricaConjecture(n);
return 0;
}
Output:
2 0.317837
3 0.504017
5 0.409683
7 0.670873
11 0.288926
13 0.517554
17 0.235793
19 0.436933
23 0.589333
29 0.1826
31 0.514998
37 0.320362
41 0.154314
43 0.298216
47 0.424455
53 0.401036
59 0.129104
...
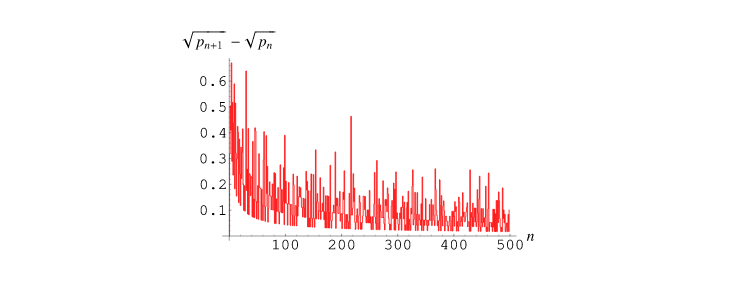
These results can be easily placed in a graph to demonstrate the heuristic behaviour.