Mersenne prime numbers

When 2^n -1 is prime, it is said to be a Mersenne prime. In this article, we have explored this concept of Mersenne prime numbers in depth along with algorithms + implementations to find Mersenne prime numbers.

Table of contents

1. Definitions
2. Algorithm
3. Time complexity
4. A way of implementation
5. The Lucas-Lehmer Test

1. Definitions

A prime number is a number that is only divisible to 1 and itself.

The first few primes are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …

Notice that 1 is not part of this series.

There is no mathematician who has not been looking at the prime numbers. Each one in his own style.

Many early writers felt that the numbers of the form 2^n -1 were prime for ALL primes n.

In 1536 Hudalricus Regius showed that 2^11 - 1 = 2047 was not prime (it is 23*89).

By 1603 Pietro Cataldi had correctly verified that 2^17 - 1 and 2^19 - 1 were both prime, but then incorrectly stated 2^n - 1 was also prime for 23, 29, 31 and 37.

In 1640 Fermat showed Cataldi was wrong about 23 and 37; then Euler in 1738 showed Cataldi was also wrong about 29. Sometime later Euler showed Cataldi's assertion about 31 was correct.

Enter French monk Marin Mersenne (1588-1648) stated in the preface to his Cogitata Physica-Mathematica (1644) that the numbers 2^n -1 were prime for

n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 and 257

and were composite for all other positive integers n < 257. Mersenne's (incorrect) conjecture fared only slightly better than Regius', but still got his name attached to these numbers.

Definition: When 2^n -1 is prime, it is said to be a Mersenne prime.

It was obvious to Mersenne's peers that he could not have tested all of these numbers (in fact he admitted as much), but they could not test them either.

It was not until over 100 years later, in 1750, that Euler verified the next number on Mersenne's and Regius' lists, 2^31 -1 , was prime.

After another century, in 1876, Lucas verified 2^127 -1 was also prime.

Seven years later Pervouchine showed 2^61 -1 was prime, so Mersenne had missed this one.

In the early 1900's Powers showed that Mersenne had also missed the primes 2^89 -1 and 2^107 -1 .

Finally, by 1947 Mersenne's range, n < 258, had been completely checked and it was determined that the correct list is:

n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 and 127. (1)

2. Algorithm

Since the Mersenne prime numbers are using the prime numbers, the only thing that we need to implement is to generate the prime numbers series.

If you are a beginner in programming if you want to check if a number is prime you might want to use a simple loop to check for all numbers between 2 and the square root of it !

    procedure isPrime(n)
        loop
            i <- 2..sqrt(n) 
            if (n mod i == 0) return false
        end loop
        return true

This check might be time consumming and double checking. Why ? because you start checking from number 2 and continue until you reach the square root number. But in this subset there might be other numbers that are divided with other prime numbers so there is no need to check for them again !

To avoid this situation we can use an array to store the previous checked prime numbers, i.e. we only divide the given number to the prime numbers before it, this method is called memoaization.

    procedure isPrime(array p, n)
        i <- 0
        while p[i] <= sqrt(n)
            if (n mod p[i] == 0) return false
            
        return true

    procedure generatePrime(n)
        array p
        j <- 0

        for i <- 3..n-1
            if (isPrime(p, i)) 
                {
                p[j] <- i
                j <- j + 1
                }

Another way is to use the sieve of Eratosthenes , the sieve of Sundaram or the sieve of Atkin

3. Time complexity

Since we check all the numbers the generatePrime function will be O(N).
For the isPrime function we check only for the prime numbers before the square root of N, which depends on the size of the subset of the prime numbers which means usually O(log N)
So, generating the prime series will be O(N logN)

4. A way of implementation

In the next implementation we are going to generate the first Mersenne prime numbers.
Because 2^n is a long number we will use the long double type which will represent a number on 64 bits ~ 18 billion billion.
So, we will generate prime numbers for the first 2^20 numbers and after that for each one of it we will check if it is a Mersenne prime or not.

The function isPrime is not using the mod expresion to retrive the rest as it was implemented in the Cramer's conjecture. And that is because the mod refers only to integers, and since we use floating point data type, an error at compilation arrise. To avoid that we will use a small programming trick: if the difference from the ceil division and the division is 0 then we know for sure there is no rest ! You can try to modify the program and use the fmod or remainder instead.

If 2^r * 2^p = 2^(r+p) and r=p then sqrt(2^(r+r)) = 2^r which makes the valid the interval of checking if a number is prime.

#include <iostream>
#include <math.h>

using namespace std;

bool isPrime(long double *p, long double n)
{
    long double sqrtn = sqrt(n);
    
    unsigned int i=0;
    
    long double result;
    
    while ( p[i] <= sqrtn )
        {
            result = n / p[i++] ;
        
            if(ceil(result) - result == 0) return false; 
        }
    return true;
}

long double & generatePrime(long double n, unsigned int &size)
{
    unsigned int i, j;
    long double *p = new long double [ (unsigned long long)n ];
    
    j = 0;
    p[j++] = 2;
    
    for (i=3; i < n; i++)
        if(isPrime(p, i)) p[j++] = i;
        
    size = j;   
    
    return *p;
}

void checkMersenePrime(int n)
{
    unsigned int i=0, size;
    
    long double *p = &generatePrime(pow(2,n),size);

    while (i < 100)
        cout << "2^"<< p[i]<<"-1 "<< (isPrime(p, pow(2,p[i]) - 1 )?"Mersenne Prime":"") << endl,i++;
}

int main()
{
    int n = 20;
    
    checkMersenePrime(n);
    
    return 0;
}

Output:

2^2-1 Mersenne Prime
2^3-1 Mersenne Prime
2^5-1 Mersenne Prime
2^7-1 Mersenne Prime
2^11-1
2^13-1 Mersenne Prime
2^17-1 Mersenne Prime
2^19-1 Mersenne Prime
2^23-1
2^29-1
2^31-1 Mersenne Prime
2^37-1
2^41-1
2^43-1
2^47-1
2^53-1
2^59-1
2^61-1 Mersenne Prime
2^67-1
2^71-1
2^73-1
2^79-1
2^83-1
2^89-1
2^97-1
2^101-1
...

You can try to generate all the primes for the first 2^20 numbers to see what compiler gives you as a result.
This is the output from an online cpp compiler (2)
where first column is the prime number and the second one is in the form of 2^p - 1

2 3
3 7
5 31
7 127
11 2047
13 8191
17 131071
19 524287
23 8388607
29 536870911
31 2147483647
37 137438953471
41 2199023255551
43 8796093022207
47 140737488355327
53 9007199254740991
59 576460752303423487
61 2305843009213693951
67 147573952589676412928
71 2361183241434822606848
73 9444732965739290427392
79 604462909807314587353088
83 9671406556917033397649408
89 618970019642690137449562112
97 158456325028528675187087900672
101 2535301200456458802993406410752

Observations:
1. Do you notice something strange ? until 67 prime number the compiler subtracts 1 after that it does not, and that is because of the data type memory allocation.
2. Except for the first Mersenne prime number which is 3 the other numbers are ending in 7 or 1 which makes them compatible to be prime as well. Maybe that was making Regius to show the contrary of the 2^11 - 1.

5. The Lucas-Lehmer Test (LLT)

Another way to check Mersenne primes is to use the LLT.
The test is based on a theorem developped by Édouard Lucas in 1876 and improved by Derrick Henry Lehmer in the 1930s.

Theorem: For p an odd prime, the Mersenne number 2^p-1 is prime if and only if 2^p-1 divides S(p-1) where S(n+1) = S(n)^2-2, and S(1) = 4.

In other words he defined a sequence of numbers in the form

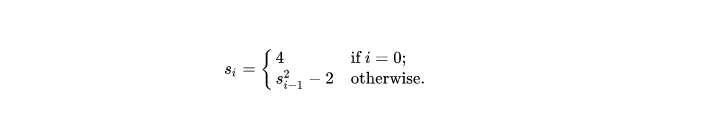
where i >= 0.

The first numbers in the sequence are: 4, 14, 194, 37634...

The LLT pseudo-code

    // Determine if Mp = 2p − 1 is prime for p > 2
    Lucas–Lehmer(p)
        s <- 4
        repeat p − 2 times:
            s = ((s × s) − 2) mod (2^p-1)
        if s == 0 return PRIME else return COMPOSITE

We can rewrite the checkMersenePrime to the LLT to generate all the Mersenne primes. Notice the using of fmod function for double data types.

    void checkMersenePrime(int n)
    {
        unsigned int i=0, j=1, size;

        long double *p = &generatePrime(pow(2,n),size);

        long double s;

        while (j < size)
            {   s = 4;
                for (i=0; i < p[j]-2; i++)
                    s = fmod(s*s - 2, pow(2,p[j])-1 );

                if (s == 0)
                    cout<< "2^"<<p[j] << "-1 Mersenne prime"<< endl; 

                j++;    
            }
    }

Output:

2^3-1 Mersenne prime
2^5-1 Mersenne prime
2^7-1 Mersenne prime
2^13-1 Mersenne prime
2^17-1 Mersenne prime
2^19-1 Mersenne prime
2^31-1 Mersenne prime

Case by case example for p = 3,5 and 7

    p = 3 => i = [0,1) 
       => s = (4*4 - 2) mod (2^3-1) = 0
    
    p = 5 => i = [0,3) 
       => s = (4*4 - 2) mod (2^5-1) = 14
          s = (14*14 - 2) mod (2^5-1) = 8
          s = (8*8 - 2) mod (2^5-1) = 0
           
    p = 7 => i = [0,5) 
        => s = (4*4 - 2) mod (2^7-1) = 14
           s = (14*14 - 2) mod (2^7-1) = 67
           s = (67*67 - 2) mod (2^7-1) = 42
           s = (42*42 - 2) mod (2^7-1) = 111
           s = (111*111 - 2) mod (2^7-1) = 0

The Lucas–Lehmer test is the one of the main primality tests used by the Great Internet Mersenne Prime Search (GIMPS) to locate large primes. This search has been successful in locating many of the largest primes known to date.