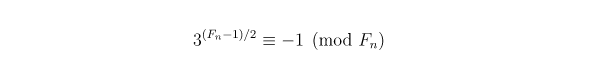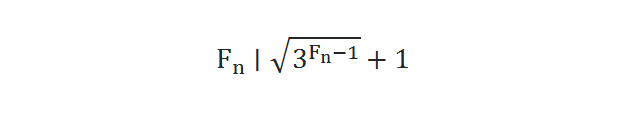Fermat number and Pepin's test

In this article, we have explored the concept of Fermat number, demonstrated C++ implementations to compute and verify fermat number and explained Pepin's test for Fermat number.

Table of contents

1. Definitions
2. Algorithm
3. Time complexity
4. A way of implementation
5. Pepin's test

1. Definitions

A prime number is a number that is only divisible to 1 and itself.

The first few primes are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …

Notice that 1 is not part of this series.

There is no mathematician who has not been looking at the prime numbers. Each one in his own style.

Pierre de Fermat wrote to Marin Mersenne on December 25, 1640 that:
"If I can determine the basic reason why 3, 5, 17, 257, 65537, ..., are prime numbers, I feel that I would find very interesting results, for I have already found marvelous things [along these lines] which I will tell you about later." 1

With these words we can interpret that he was looking for a mathematical form to represent these numbers.

Definition: When 2^2^n +1 is prime, it is said to be a Fermat number.

The only known Fermat primes are the first five Fermat numbers: F0=3, F1=5, F2=17, F3=257, and F4=65537. A simple heuristic shows that it is likely that these are the only Fermat primes (though many folks like Eisenstein thought otherwise).

2. Algorithm

Since the Mersenne prime numbers are using the prime numbers, the only thing that we need to implement is to generate the prime numbers series.

If you are a beginner in programming if you want to check if a number is prime you might want to use a simple loop to check for all numbers between 2 and the square root of it !

    procedure isPrime(n)
        loop
            i <- 2..sqrt(n) 
            if (n mod i == 0) return false
        end loop
        return true

This check might be time consumming and double checking. Why ? because you start checking from number 2 and continue until you reach the square root number. But in this subset there might be other numbers that are divided with other prime numbers so there is no need to check for them again !

To avoid this situation we can use an array to store the previous checked prime numbers, i.e. we only divide the given number to the prime numbers before it, this method is called memoaization.

    procedure isPrime(array p, n)
        i <- 0
        while p[i] <= sqrt(n)
            if (n mod p[i] == 0) return false
            
        return true

    procedure generatePrime(n)
        array p
        j <- 0

        for i <- 3..n-1
            if (isPrime(p, i)) 
                {
                p[j] <- i
                j <- j + 1
                }

Another way is to use the sieve of Eratosthenes, the sieve of Sundaram or the sieve of Atkin

3. Time complexity

Since we check all the numbers the generatePrime function will be O(N).
For the isPrime function we check only for the prime numbers before the square root of N, which depends on the size of the subset of the prime numbers which means usually O(log N)
So, generating the prime series will be O(N logN)

4. A way of implementation

In the next implementation we are going to generate the first Fermat numbers.
Because 2^2^n is a long number we will use the long double type which will represent a number on 64 bits ~ 18 billion billion.
So, we will generate prime numbers for the first 2^20 numbers and after that for each one of it we will check if it is a Fermat number or not.

The function isPrime is not using the mod expresion to retrive the rest as it was implemented in the Cramer's conjecture. And that is because the mod refers only to integers, and since we use floating point data type, an error at compilation arrise. To avoid that we will use a small programming trick: if the difference from the ceil division and the division is 0 then we know for sure there is no rest ! You can try to modify the program and use the fmod or remainder instead.
isinf is used to check when n is infinit or not, and it is usefull in the conditional clause when we output the result. If we do not write this condition then isPrime will return true in all cases when n is infinit.

If 2^r * 2^p = 2^(r+p) and r=p then sqrt(2^(r+r)) = 2^r which makes the valid the interval of checking if a number is prime.

#include <iostream>
#include <math.h>
#include <iomanip>

using namespace std;

bool isPrime(long double *p, long double n)
{
    long double sqrtn = sqrt(n);
    
    unsigned int i=0;
    
    long double result;
    
    while ( p[i] <= sqrtn )
        {
            result = n / p[i++] ;
        
            if(ceil(result) - result == 0) return false; 
        }
    return !isinf(n);
}

long double & generatePrime(long double n, unsigned int &size)
{
    unsigned int i, j;
    long double *p = new long double [ (unsigned long long)n ];
    
    j = 0;
    p[j++] = 2;
    
    for (i=3; i < n; i++)
        if(isPrime(p, i)) p[j++] = i;
        
    size = j;   
    
    return *p;
}

void checkFermatNumber(int n)
{
    unsigned int i=0, size;
    long double f;
    long double *p = &generatePrime(pow(2,n),size);

    while (i < n)
        f = pow(2,pow(2,i)) + 1,
        cout<<fixed<<setprecision(0)<< "2^2^"<< i<<"+1= "<<f<< (isPrime(p, f )?" Fermat number F" + to_string(i):"") << endl,
        i++;
}

int main()
{
    int n = 20;
    
    checkFermatNumber(n);
    
    return 0;
}

Output:

2^2^0+1= 3 Fermat number F0
2^2^1+1= 5 Fermat number F1
2^2^2+1= 17 Fermat number F2
2^2^3+1= 257 Fermat number F3
2^2^4+1= 65537 Fermat number F4
2^2^5+1= 4294967297
2^2^6+1= 18446744073709551616
2^2^7+1= 340282366920938463463374607431768211456
2^2^8+1= 1157920892373161954235709850086879078532699846656405640394575840079131
29639936
2^2^9+1= 1340780792994259709957402499820584612747936582059239337772356144372176
4030073546976801874298166903427690031858186486050853753882811946569946433649006
084096
2^2^10+1= inf
2^2^11+1= inf
2^2^12+1= inf
2^2^13+1= inf
2^2^14+1= inf
2^2^15+1= inf
2^2^16+1= inf
2^2^17+1= inf
2^2^18+1= inf
2^2^19+1= inf

5. Pepin's test

There’s a specialized test for checking whether a Fermat number is prime, Pépin’s test. It says that for n ≥ 1, the Fermat number Fn is prime if and only if

in other words Fn needs to be divisible with Pepin's number:

We can translate this into the next program:

    #include <iostream>
    #include <cmath>

    using namespace std;

    long double pepinTest(int n)
    {
        long double Fn = pow(2,pow(2,n)) + 1;
        long double p = sqrt(pow(3,(Fn-1))) + 1;
        long double result = p / Fn;

        return  ceil(result) - result ;
    }

    int main()
    {
        long double pepin_value;

        for (int i = 1; i<=15; i++)
            {
                pepin_value = pepinTest(i);

                if(isfinite(pepin_value))
                    if( pepin_value == 0) cout <<"F"<<i<<" prime"<<endl;
                    else cout <<"F"<<i<<" composite"<<endl;
            }

        return 0;
    }

Output:

F1 prime
F2 prime
F3 prime

The downside of Pepin's test is that it needs to work with very long numbers. As we could see from this example even though the for statement loops for 15 times the result is only for 3 Fermat numbers.

Again, to show if a number is divisible with another one we have used the a small programming trick by invoking the ceil math function.
Because the result variable might have nan values we have used isfinite function to check that.