
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 3 minutes
Algorithm
Sieve of Eratosthenes is a simple and ancient algorithm (over 2200 years old) used to find the prime numbers up to any given limit. It is one of the most efficient ways to find small prime numbers (<= $10^8$).
For a given upper limit the algorithm works by iteratively marking the multiples of primes as composite, starting from 2. Once all multiples of 2 have been marked composite, the muliples of next prime, ie 3 are marked composite. This process continues until $p < \sqrt(N)$ where is a prime number.
This algorithm was devised by Eratosthenes, a greek mathematician, astronomer, poet, geographer. Erathosthenes was born in 276 BC, so this method was over 2200 years old. Therefore it is many times called the ancient efficient method for primes and it is still used heavily today.
Sift the Two's and Sift the Three's,
The Sieve of Eratosthenes.
When the multiples sublime,
The numbers that remain are Prime.
Pseudocode
The pseudocode of The sieve of Eratosthenes algorithm is as follows:
find primes up to N
For all numbers a : from 2 to sqrt(n)
IF a is unmarked THEN
a is prime
For all multiples of a (a < n)
mark multiples of as composite
All unmarked nummbers are prime!
Example
Find list of prime numbers from 2 to 20
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
The first number in the list is 2;
Cross out every 2nd number in the list after 2 by counting up from 2 in increments of 2
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
The first number in the list after 2 is 3;
Cross out every 3rd number in the list after 3 by counting up from 3 in increments of 3
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
The first number in the list after 3 is 5;
Cross out every 5th number in the list after 5 by counting up from 5 in increments of 5
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
All numbers not crossed out are prime numbers.
We went upto 5 as the celing of square root of 20 is 5.
Prime numbers from 2 to 20 are:
2 3 5 7 11 13 17 19
Visual Example
Let us see an example -
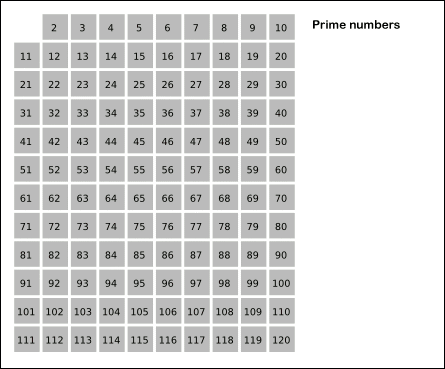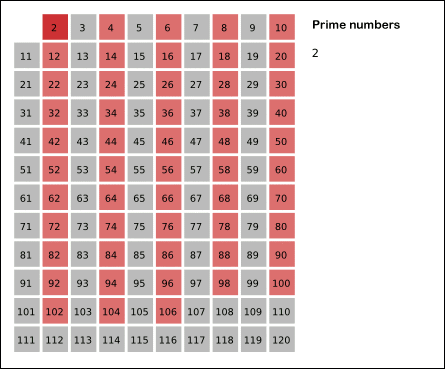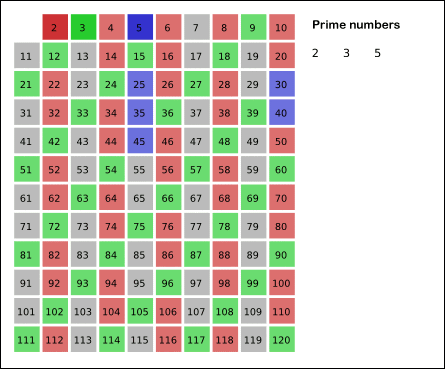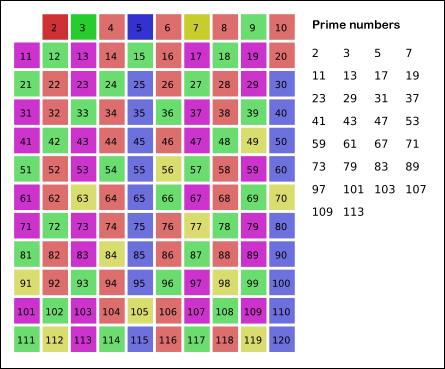
**Steps** :-
* Write down the numbers(starting with 2)
* Start traversing through all unmarked numbers. The first unmarked we see is 2
* Mark 2(prime) and mark all multiples of 2(with different colors)
* Repeat the step for number 3
* Notice that 6 is already marked so we can start at the square of the number 3 and so on for number 5, number 7, ....
Complexity
The time and space complexity of The Sieve of Eratosthenes algorithm is as follows:
- Worst case time complexity:
Θ(N log log N) - Average case time complexity:
Θ(N log log N) - Best case time complexity:
Θ(N log log N) - Space complexity:
Θ(N)
Implementations
Implementations of The Sieve of Eratosthenes algorithm in 9 different languages that is C, C++, C Sharp, Java, Go, Haskell, JavaScript, PHP and Python.
- C
- C++
- CSharp
- Java
- Go
- Haskell
- JavaScript
- PHP
- Python
C
#include <stdio.h>
#include <stdlib.h>
/* Part of Cosmos by OpenGenus Foundation */
int sieve_of_eratosthenes(int **primes, const int max) {
// Allocate memory
int *isPrime = (int *)malloc(sizeof(int) * (max + 1));
int i;
// Assume all numbers to be prime initially
for(i = 0; i <= max; ++i)
isPrime[i] = 1;
// 0 and 1 are not prime
isPrime[0] = 0;
isPrime[1] = 0;
// Maintain a count of primes as we encounter them
int count = 0;
// We need a count of all primes as we move
// This means we cannot iterate to root(max)
for(i = 2; i <= max; ++i)
{
if(isPrime[i] == 1)
{
++count;
int j;
// Set all multiples of i as not prime
for(j = 2 * i; j <= max; j += i)
isPrime[j] = 0;
}
}
*primes = (int *)malloc(sizeof(int) * count);
int j = 0;
for(i = 0; i <= max; ++i)
{
if(isPrime[i] == 1)
{
(*primes)[j++] = i;
}
}
return count;
}
int main() {
int n = 100, i;
int *primes = NULL;
// Find primes up to n
int size = sieve_of_eratosthenes(&primes, n);
printf("Primes up to %d are:\n", n);
for(i = 0; i < size; ++i)
{
printf("%d\n", primes[i]);
}
return 0;
}
C++
#include <iostream>
#include <vector>
using namespace std;
// Part of Cosmos by OpenGenus Foundation
void SieveOfEratosthenes(int n)
{
// Create a boolean array "prime[0..n]" and initialize
// all entries it as true. A value in prime[i] will
// finally be false if i is Not a prime, else true.
vector<bool> prime(n + 1, true);
for (int p = 2; p * p <= n; p++)
// If prime[p] is not changed, then it is a prime
if (prime[p] == true)
// Update all multiples of p
for (int i = p * 2; i <= n; i += p)
prime[i] = false;
// Print all prime numbers
for (int p = 2; p <= n; p++)
if (prime[p])
cout << p << " ";
}
// Driver Program to test above function
int main()
{
int n;
cout << "Enter the number";
cin >> n;
cout << "Following are the prime numbers smaller "
<< " than or equal to " << n << endl;
SieveOfEratosthenes(n);
cout << "\n";
return 0;
}
CSharp
using System;
using System.Linq;
namespace OpenGenus
{
// Part of Cosmos by OpenGenus Foundation
class Program
{
public static void Main(string[] args)
{
var random = new Random();
var n = random.Next(1, 1000);
var primes = SieveOfEratosthenes(n);
Console.WriteLine($"Primes up to {n}\n");
Console.WriteLine(string.Join(",", primes));
Console.ReadLine();
}
private static int[] SieveOfEratosthenes(int n)
{
// create number list from 0 to n
var numbers = Enumerable.Range(0, n + 1).Select(x => x).ToArray();
var lenRoot = Math.Sqrt(n);
// go through all possible factors of numbers in the range bound inclusive by 2 and n
for (var i = 2; i <= lenRoot; i++)
{
// skip numbers already blanked by a prime factor
if (numbers[i] == 0)
continue;
for (int j = i * i; j < numbers.Length; j += i)
{
// blank out any multiple of i
numbers[j] = 0;
}
}
// return all numbers between 2 and n
// these will be all primes in the range
return numbers.Where(x => x > 1).ToArray();
}
}
}
Java
/* Part of Cosmos by OpenGenus Foundation */
import java.util.Scanner; //To take the input the scanner class has to be imported.
public class erathosthenes{
public void sieve (int n) {
boolean checkPrime[] = new boolean [n+1]; //checkPrime array to mark the elements whether they are prime or not.
int a=2;
for(int i=0; i<n; i++){ //initialises all elements of checkPrime to true
checkPrime[i] = true;
}
for(int i=a ; i*i<=n ; i++){ //outer for loop is to check whether a particular element has been marked, if no then it is taken
if(checkPrime[i] == true){
for(int j=i*2 ; j<=n ; j=j+i){ // inner for loop marks the multiples of the element selected by the outer for loop
checkPrime[j] = false;
}
}
}
for(int i=2 ; i<=n ; i++){
if(checkPrime[i] == true)
System.out.println(i+" ");
}
}
public static void main(String [] args){
System.out.println("Enter the upperBound:");
Scanner s=new Scanner(System.in);
int n=s.nextInt();
erathosthenes ee = new erathosthenes();
ee.sieve(n);
}
}
Go
package main
import "fmt"
// Part of Cosmos by OpenGenus Foundation
func SieveOfEratosthenes(n int) []int {
//Create an array of Boolean values indexed by
//integers 2 to n, initially all set to true.
integers := make([]bool, n+1)
for i := 2; i < n+1; i++ {
integers[i] = true
}
for i := 2; i*i <= n; i++ {
if integers[i] == true {
//Check all multiples of i
for j := i * 2; j <= n; j += i {
integers[j] = false
}
}
}
//Return all unchanged numbers (prime numbers) <= n
var primes []int
for i := 2; i <= n; i++ {
if integers[i] == true {
primes = append(primes, i)
}
}
return primes
}
Haskell
module Eratosthenes where
-- Part of Cosmos by OpenGenus Foundation
eratosthenes :: [Integer] -- A list of all prime numbers
eratosthenes = go [2..]
where
-- If we have something in the front of the list (x:xs),
-- we know it wasn't filtered, so it's prime.
-- Then, we filter the rest of the list to exclude multiples of
-- that number.
go (x:xs) = x : (go $ filter (\n -> n `mod` x /= 0) xs)
primes = eratosthenes
main = do
n <- getLine
print $ take (read n :: Int) primes
JavaScript
class SieveOfEratosthenes {
/**
* @constructor
* @param {number} max - max number to test up to
* Part of Cosmos by OpenGenus Foundation
*/
constructor(max) {
this._max = max;
this._sqrtMax = Math.ceil(Math.sqrt(this._max));
// Get an array from number 2 up to max. Start from 2 because 0 and 1
// are not primes and do not need to be evaluated.
this._storage = Array.from({ length: max - 1 }, (k, v) => v + 2 );
}
_isPrime(num) {
for (let i = 2; i < this._sqrtMax; i++) {
if (num % i === 0 && num !== i) {
return false;
}
}
return true;
}
/**
* start - determine all primes
* @return {array} an array of all prime numbers from 2 to max.
*/
start() {
this._storage = this._storage.filter(num => {
return this._isPrime(num);
});
return this._storage;
}
}
////////////
// TESTS: //
////////////
// All valid prime numbers up to 1000
const primeNums = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53,
59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137,
139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223,
227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307,
311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397,
401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487,
491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593,
599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677,
683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787,
797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883,
887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997];
// Test cases:
// All test cases should return "test-X is true"
const testNums = [1, 30, 100, 300, 600, 1000]
testNums.forEach((max, idx) => {
const sieve = new SieveOfEratosthenes(max);
const allPrimes = sieve.start();
const diff = allPrimes.filter(num => {
return primeNums.indexOf(num) === -1;
});
console.log(`test-${idx} is ${diff.length === 0}`)
})
PHP
<?php
/**
* Part of Cosmos by OpenGenus Foundation
*
* Find all prime numbers up to any given n using Sieve of Eratosthenes.
*
* @param int $n
*
* @return array|integer
*/
function sieveOfEratosthenes($n)
{
if ($n <= 1) {
return -1;
}
$array = array_fill_keys(range(2, $n), true);
for ($i = 2; $i <= (int) sqrt($n); $i++) {
if ($array[$i] === true) {
for ($j = $i ** 2; $j <= $n; $j += $i) {
$array[$j] = false;
}
}
}
return array_keys($array, true);
}
echo implode(', ', sieveOfEratosthenes(365));
Python
import sys
# Part of Cosmos by OpenGenus Foundation
def sieve_erato(n):
loops = 0
numbers = set(range(2, n))
for i in range(2, int(n ** 0.5) + 1):
for j in range(i * 2, n, i):
numbers.discard(j)
loops += 1
return sorted(numbers), loops
try:
primes = sieve_erato(int(input().rstrip()))
except:
sys.exit()
print(primes[0])
print("\nComputations {}".format(primes[1]))
Applications
Prime numbers are very crucial and forms the basis of some of the most wonderful Mathematical discoveries. Thus, it is very important to compute prime numbers quickly.
The Sieve of Eratosthenes algorithm has the advantage of being simple to code and fast on execution.
This algorithm can be used in the following cases:
- Determine whether a number N is a prime number or not
- Factorize a number N
- Find all prime numbers within a range N to M
- Prove prime number theorems for a range like Goldbach’s Conjecture.
Questions
Which complexity theory class does The Sieve of Eratosthenes belong to?
Why is Sieve of Eratosthenes efficient than most other simple algorithms
In the naive method, you do $O(\sqrt(N))$ operations for each number num you check for primality. This is $O( N * \sqrt(N))$ in total.
In the sieve method, for each unmarked number from 1 to N, we do N / 2 operations when marking multiples of 2, N / 3 when marking those of 3, N / 5 when marking those of 5 etc. This is N * (1/2 + 1/3 + 1/5 + 1/7 + ...), which is $O(N * log(log(N)))$. See here for that result.
So the asymptotic complexity is not the same. Even a naive sieve will beat the naive prime-generation method. Optimized versions of the sieve can get much faster, but the big-oh remains unchanged.
