
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 5 minutes
The GCD of two integers X and Y is the largest integer that divides both of X and Y (without leaving a remainder). Greatest Common Divisor is, also, known as greatest common factor (gcf), highest common factor (hcf), greatest common measure (gcm) and highest common divisor.
Key Idea: Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number.
Example: GCD(20, 15) = GCD(15, 10) = 5
Algorithm
The Euclidean Algorithm for calculating GCD of two numbers A and B can be given as follows:
-
If A=0 then GCD(A, B)=B since the Greatest Common Divisor of 0 and B is B.
-
If B=0 then GCD(a,b)=a since the Greates Common Divisor of 0 and a is a.
-
Let R be the remainder of dividing A by B assuming A > B. (R = A % B)
-
Find GCD( B, R ) because GCD( A, B ) = GCD( B, R ). Use the above steps again.
Sample calculation
Sample calculation of Greatest Common Divisor of 2 numbers using Euclidean Algorithm is as follows:
Greatest Common Divisor of 285 and 741
We have to calculate GCD (285, 741)
As 285 is less than 741, we need to calculate GCD (741, 285)
GCD (285, 741) = GCD (741, 285)
Now, remainder of dividing 741 by 285 is 171.
Therefore, we need to calculate GCD (285, 171)
GCD (285, 741) = GCD (741, 285) = GCD (285, 171)
Now, remainder of dividing 285 by 171 is 114.
Therefore, we need to calculate GCD (171, 114)
GCD (285, 741) = GCD (741, 285) = GCD (285, 171) = GCD (171, 114)
Now, remainder of dividing 171 by 114 is 57.
Therefore, we need to calculate GCD (114, 57)
GCD (285, 741) = GCD (741, 285) = GCD (285, 171) = GCD (171, 114) = GCD (114, 57)
Now, remainder of dividing 114 by 57 is 0.
Therefore, we need to calculate GCD (57, 0)
As B=0, GCD( 57, 0) = 57.
GCD (285, 741) = GCD (741, 285) = GCD (285, 171) = GCD (171, 114) = GCD (114, 57) = GCD (57, 0) = 57
Therefore, Greatest Common Divisor of 285 and 741 is 57.
Flowchart for the algorithm
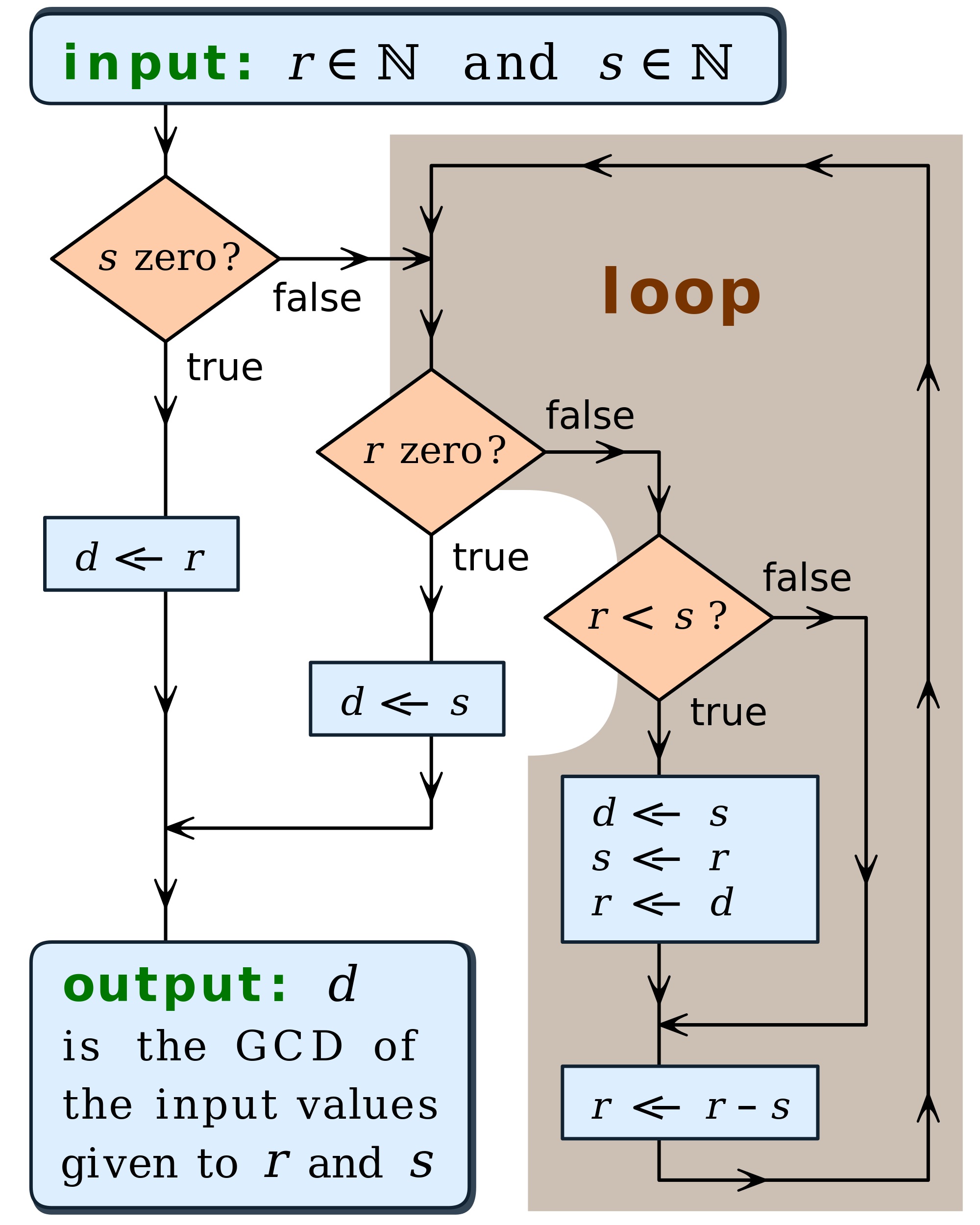
Pseudocode
function gcd(A,B):
if (A < B):
return gcd(B,A)
if (A = 0):
return B
return gcd(B, A%B)
Complexity
-
Worst case time complexity : O(log(min(A,B))
-
Average case time complexity : O(log A)
-
Best case time complexity : O(1)
Explanation/ Derivation of complexity for Euclidean Algorithm:
Let $T(a,b)$ be the number of steps taken in the Euclidean algorithm, which repeatedly evaluates $\gcd(a,b)=\gcd(b,a\bmod b)$ until $b=0$, assuming $a\geq b$.
Let $h=\log_{10}b$ be the number of digits in $b$ . (assuming the time-complexity of the $\mathrm{mod}$ function to be $O(1)$.
- Worst Case scenario
$a=F_{n+1}$ and $b=F_n$, where $F_n$ is the Fibonacci sequence, since it will calculate $\gcd(F_{n+1},F_n)=\gcd(F_n,F_{n-1})$ until it gets to $n=0$, so $T(F_{n+1},F_n)=\Theta(n)$ and $T(a,F_n)=O(n)$. Since $F_n=\Theta(\varphi^n)$, this implies that $T(a,b)=O(\log_\varphi b)$. Note that $h\approx log_{10}b$ and $\log_bx={\log x\over\log b}$ implies $\log_bx=O(\log x)$ for any $a$, so the worst case for Euclid's algorithm is $O(\log_\varphi b)=O(h)=O(\log b)$.
- Average case scenario
If $a$ is fixed and $b$ is chosen uniformly from $\mathbb Z\cap[0,a)$, then the number of steps $T(a)$ is
$$T(a)=-\frac12+6\frac{\log2}\pi(4\gamma-24\pi^2\zeta'(2)+3\log2-2)+{12\over\pi^2}\log2\log a+O(a^{-1/6+\epsilon}),$$
or, for less accuracy, $T(a)={12\over\pi^2}\log2\log a+O(1)$
- Best case scenario
$a=b$ or $b=0$ or some other convenient case like that happens, so the algorithm terminates in a single step. Thus, $T(a,a)=O(1)$.
If we are working on a computer using 32-bit or 64-bit calculations, as is common, then the individual $\bmod$ operations are in fact constant-time, so these bounds are correct. If, however, we are doing arbitrary-precision calculations, then in order to estimate the actual time complexity of the algorithm, we need to use that $\bmod$ has time complexity $O(\log a\log b)$. In this case, all of the "work" is done in the first step, and the rest of the computation is also $O(\log a\log b)$, so the total is $O(\log a\log b)$. I want to stress, though, that this only applies if the number is that big that you need arbitrary-precision to calculate it.
Implementations
Following are the implementation of Euclidean Algorithm in 10 different languages such as Python, C, C++, Java, CSharp, Erlang, Go, JavaScript, PHP and Scala.
- Python
- C
- C++
- Java
- CSharp
- Erlang
- Go
- JavaScript
- PHP
- Scala
Python
# Python applications of Euclidean Algorithm
def gcd(a,b):
'''The GCD Calculation function'''
if a == 0:
return b
if b == 0:
return a
return gcd(b, a%b)
# Utility code to test this gcd function:
a=10,b=26
print ("GCD of {} and {} is {}".format(a, b, gcd(a,b)))
# prints gcd as 2
a=1831,b=0
print ("GCD of {} and {} is {}".format(a, b, gcd(a,b)))
# prints gcd as 1831
a=11024,b=32424
print ("GCD of {} and {} is {}".format(a, b, gcd(a,b)))
# prints gcd as 8
C
// A simple implementation of eucliedan algorithm in C
#include
int GCD (int x, int y)
{
if (x == 0)
return y;
return gcd(y%xx);
}
// Driver program to test above function
int main()
{
int a = 100, b = 15;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
a = 35, b = 0;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
a = 31, b = 20;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
return 0;
}
C++
#include <stdio.h>
#include <algorithm>
// Part of Cosmos by OpenGenus Foundation
int gcd(int x, int y)
{
while (y > 0)
{
x %= y;
std::swap(x, y);
}
return x;
}
int lcm(int x, int y)
{
return x / gcd(x, y) * y;
}
int main()
{
int a, b;
scanf("%d %d", &a, &b);
printf("GCD = %d\n", gcd(a, b));
printf("LCM = %d", lcm(a, b));
}
Java
import java.util.*;
// Part of Cosmos by OpenGenus Foundation
class Gcd_Calc{
public int determineGCD(int a, int b) {
while (b > 0)
{
int r = a % b;
a = b;
b = r;
}
return a;
}
public static void main(String[] args) {
Gcd_Calc obj = new Gcd_Calc();
System.out.println("Enter two nos: ");
Scanner s1 = new Scanner(System.in);
int a = s1.nextInt();
int b = s1.nextInt();
int gcd = obj.determineGCD(a, b);
System.out.println("GCD = " + gcd);
}
}
C#
using System;
namespace gcd_and_lcm
{
class gcd_lcm
{
int a, b;
public gcd_lcm(int number1,int number2)
{
a = number1;
b = number2;
}
public int gcd()
{
int temp1 = a, temp2 = b;
while (temp1 != temp2)
{
if (temp1 > temp2)
{
temp1 -= temp2;
}
else
{
temp2 -= temp1;
}
}
return temp2;
}
public int lcm()
{
return a * b / gcd();
}
}
class Program
{
static void Main(string[] args)
{
int a = 20, b = 120;
gcd_lcm obj = new gcd_lcm(a, b);
Console.WriteLine("GCD of {0} and {1} is {2}", a, b, obj.gcd());
Console.WriteLine("LCM of {0} and {1} is {2}", a, b, obj.lcm());
Console.ReadKey();
}
}
}
Erlang
% Part of Cosmos by OpenGenus Foundation
-module(gcd_and_lcm).
-export([gcd/2, lcm/2]).
gcd(X, 0) -> X;
gcd(X, Y) -> gcd(Y, X rem Y).
lcm(X, Y) -> X * Y / gcd(X, Y).
Go
package main
// Part of Cosmos by OpenGenus Foundation
import (
"fmt"
)
func calculateGCD(a, b int) int {
for b != 0 {
c := b
b = a % b
a = c
}
return a
}
func calculateLCM(a, b int, integers ...int) int {
result := a * b / calculateGCD(a, b)
for i := 0; i < len(integers); i++ {
result = calculateLCM(result, integers[i])
}
return result
}
func main() {
// 8
fmt.Println(calculateGCD(8, 16))
// 4
fmt.Println(calculateGCD(8, 12))
// 12
fmt.Println(calculateLCM(3, 4))
// 1504
fmt.Println(calculateLCM(32, 94))
// 60
fmt.Println(calculateLCM(4, 5, 6))
// 840
fmt.Println(calculateLCM(4, 5, 6, 7, 8))
}
JavaScript
function gcd(a, b) {
return b === 0 ? a : gcd(b, a % b);
}
function lcm(a, b) {
return b === 0 ? 0 : a * b / gcd(a, b);
}
// GCD
console.log(gcd(15, 2)); // 1
console.log(gcd(144, 24)); // 24
// LCM
console.log(lcm(12, 3)); // 12
console.log(lcm(27, 13)); // 351
PHP
<?php
function gcd($a, $b) {
if(!$b) {
return $a;
}
return gcd($b, $a % $b);
}
function lcm($a, $b) {
if($a || $b) {
return 0;
}
return abs($a * $b) / gcd($a, $b);
}
Scala
object gcdandlcm extends App{
def gcd(a:Int, b:Int):Int = {
while(b > 0){
val r:Int = a % b
a = b
b = r
}
a
}
def lcm(a:Int, b:Int):Int = {
var num1:Int = 0
var num2:Int = 0
var lcm:Int = 0
if(a > b){
num1 = a
num2 = b
} else {
num1 = b
num2 = a
}
for(x <- 1 to num2){
if((num1 * i) % num2 == 0){
return num1 * i
}
}
return 0
}
}
Applications
The Euclidean Algorithm is one of the most handy algorithms which one can use to speed up simple problems like calculation of Greatest Common Divisor of two numbers.
With Euclidean Algorithm, one can, efficiently, solve these problems:
- Simplify any fraction
- Find co-primes
- Find prime factors of a number
- Change numerical ranges of data that is scaling
- Arithmetic scaling of RSA Cryptosystem
