The Brocard conjecture states that the number of prime numbers lying between the squares of two consecutive prime numbers is four or more.

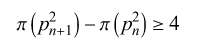
Brocad's Conjecture, in Number theory asserts that there are at least four prime numbers between (pn)^2 and (pn+1)^2, where p(n) is the nth prime number, given that n ≥ 2.

For n = 1, 2, ..., the number of prime numbers lying are 2, 5, 6, 15, 9, 22, 11, 27, 47,...

Brocard's conjecture is unproven as of today. It has been shown that it is true for large value of N = 10^4.

Table Of Contents :
1.) Introduction : Brocad's Conjecture
2.) Analysis of Brocard’s Conjecture
3.) Algorithm and Implemented Code
4.) Time Complexity
5.Conclusion

Introduction : Brocad's Conjecture

The Brocard's conjecture says that, there can be four or more prime numbers
lying between [p(n)]^2 and [p(n+1)]^2.
where,
p(n) --> is the n-th prime number.

Condition : n>=2 for all values of n.

Formula:

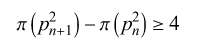
Analysis of Brocard’s Conjecture

There are two prime numbers between 4 and 9, which are 5 and 7.
There are five prime numbers between 9 and 25,
There are six prime numbers between 25 and 49.
and so on...

Given below is a list of prime numbers with all the

2, 3, 4, 5, 7, 9, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 121, 127, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 289, 293, 307, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499,....

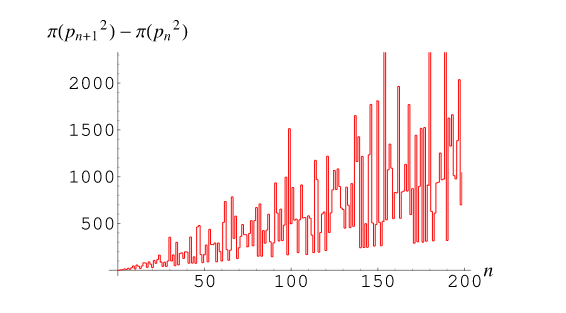
We see that the numbers in bold seem to get less in number and more apart.

A simple plot of Brocad's Conjecture (Source : Mathworld.wolfram):

Algorithm

Problem Statement :
Talking about Brocad's conjecture, we would also want to see a way to confirm that our conjecture holds true for any value of x. While we can just do some rough work and attest for the initial values, handling large numbers can become cumbersome. So, the best way will be to use the power of computer's processor and come up with an algorithm that can accomplish this task for us.

Write a program to confirm Brocad's conjecture where the user inputs the nth prime number.

Approach :
Since the user has been asked to enter the nth term. First we will write a method to find the Prime Number at the nth place namely nthPrime(). By running an optimised code where we first check if the value is possibly divisible by 2 or 3 using modulo function. And if not then check by running a for loop from 5 uptill square root of n and check the remainder. So by now we have decided on our prime number.

The next method involves for us to check how many prime number lies between the square of nth prim number and its consecutive prime square. for this again we will run a for loop with the two prime squares as the interval .And by calling the isPrime() method confirm the prime state of the number.
Separately we will maintain a counter loop every time isPrime() method returns true.

This counter will give us the count of prime number lying between [p(n)]^2 and [p(n+1)]^2, which we want to be 4 or greater.

Algorithm :

Step 1 - We write a function nPrime() to find the nth prime number for our program. We take n as input with the help of scanner.

Step 2 - We get our p(n) and p(n+1) as p1 and p2.

Step 3 - We now use the basic program to print prime numbers between two intervals where i=p1p1 and loop till i<p2p2.

Step 4 - We declare a counter variable to keep count of the prime numbers being generated every time the flag triggers true.

Step 5 - Finally we get the count of prime numbers which we see always turns out to be greater than 4.

Implemented Code

import java.util.*;

class HelloWorld {

  static int isPrime(int k) {
    if (k <= 1)
      return 0;
    if (k == 2 || k == 3)
      return 1;
    if (k % 2 == 0 || k % 3 == 0)
      return 0;
    for (int i = 5; i * i <= k; i = i + 6)
      if (k % i == 0 || k % (i + 2) == 0)
        return 0;
    return 1;
  }
  static int nThPrime(int n) {
    int i = 2;
    while (n > 0) {

      if (isPrime(i) == 1)
        n--;
      i++;
    }
    i -= 1;
    return i;
  }

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    // Declare the variables
    int n, i, j, flag;

    System.out.printf("Enter first prime number: ");
    n = sc.nextInt();

    int p1 = nThPrime(n);
    int p2 = nThPrime(n + 1);

    System.out.printf("\nPrime numbers between the square of %d and %d are: ", p1, p2);
    System.out.println();

    int counter = 0;
    for (i = p1 * p1; i <= (p2) * (p2); i++) {

      if (i == 1 || i == 0)
        continue;
      flag = 1;
      for (j = 2; j <= i / 2; ++j) {
        if (i % j == 0) {
          flag = 0;
          break;
        }
      }

      if (flag == 1) {
        counter++;
        System.out.println(i);
      }
    }
    System.out.println("Number of Prime numbers between two consecutive square of prime numbers = " + counter);

  }
}

//Output
Enter first prime number: 6
Prime numbers between the square of 13and 17 are: 
173
179
181
191
193
197199
211
223
227229
233
239
241
251
257
263
269271
277
281
283
Number of Prime numbers between two consecutive square of prime numbers = 22

Explanation of Assessment

The above output proves that the number of prime numbers between the square of 6th and 7th prime are 22 which is more than 4.
Hence Brocad's conjecture has been verified.

Time Complexity

Since two simple for loop have been used to maintain counting its order of O(n^2).

Conclusion

We saw in this article at OpenGenus how Brocard’s Conjecture works and analysed it in detail.
Also, interestingly the conjecture remains still unproven and only thanks to computational research and brute force algorithms it was verified up till n=10^4.