Sieve of Atkin

Reading time: 30 minutes

Other similar ways to calculate prime numbers using sieve techniques are:

1. Sieve of Eratosthenes
2. Sieve of Sundaram

Algorithm

• Create a list named final list and fill it with:
  • 2, 3 and 5
• Create a list named sieve list with an entry for each positive integer and intially mark them as non prime
• For each entry number N in the sieve list, find the modulo-sixty remainder r (remainder when N is divided by 60) for N:
  • If r is 1, 13, 17, 29, 37, 41, 49, or 53:
    • flip the entry for each possible solution to 4x^2 + y^2 = N.
    • All numbers with modulo-sixty remainder 1, 13, 17, 29, 37, 41, 49, or 53 have a modulo-twelve remainder of 1 or 5. These numbers are prime if and only if the number of solutions to 4×^2+y^2=n is odd and the number is square free. A square free integer is one which is not divisible by any perfect square other than 1.
  • If r is 7, 19, 31, or 43:
    • flip the entry for each possible solution to 3x^2 + y^2 = N.
    • All numbers with modulo-sixty remainder 7, 19, 31, or 43 have a modulo-six remainder of 1. These numbers are prime if and only if the number of solutions to 3x^2 + y^2 = n is odd and the number is square free.
  • If r is 11, 23, 47, or 59:
    • flip the entry for each possible solution to 3x^2 – y^2 = N when x > y.
    • All numbers with modulo-sixty remainder 11, 23, 47, or 59 have a modulo-twelve remainder of 11. These numbers are prime if and only if the number of solutions to 3x^2 – y^2 = n is odd and the number is square free.
  • If r is something else, ignore it completely.
• Start with the lowest number in the sieve list
• Take the next number in the sieve list still marked prime
• Include the number in the results list
• Square the number and mark all multiples of that square as non-prime. Note that the multiples that can be factored by 2, 3, or 5 need not be marked, as these will be ignored in the final enumeration of primes

Complexity

Sieve of Atkin:

Time complexity: Θ(N)
Space complexity: Θ(N)

The algorithm described above can compute primes up to N using O(N) operations with only O(N) bits of memory.

Sieve of Eratosthenes which uses O(N log log N) operations and the same O(N^1/2/log N) bits of memory plus a minimal page buffer.

Sieve of Atkin (modified enumerating lattice points variation)

Time complexity: Θ(N / (log log N))
Space complexity: Θ(N^0.5)

A special modified "enumerating lattice points" variation which is not the above version of the Sieve of Atkin can theoretically compute primes up to N using O( N / log log N) operations with N^1/2 + o(1) bits of memory but this variation is rarely implemented.

That is a little better in performance at a very high cost in memory as compared to both the ordinary page segmented version and to an equivalent but rarely-implemented version of the sieve of Eratosthenes which uses O(N) operations and O(N^1/2(log log N)/log N) bits of memory.

Example

Input- limit to be 20

Input numbers are:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10
11, 12, 13, 14, 15, 16, 17, 18, 19, 20.

Printing prime numbers and ignoring non-prime.
Output:

2, 3, 5, 7, 11, 13, 17, 19

Explanation

• Status for all the numbers in the start is False. Special number is 2, 3 and 5 which are known to be prime.
  • Generate Values for the conditions.(take help of the table given below).

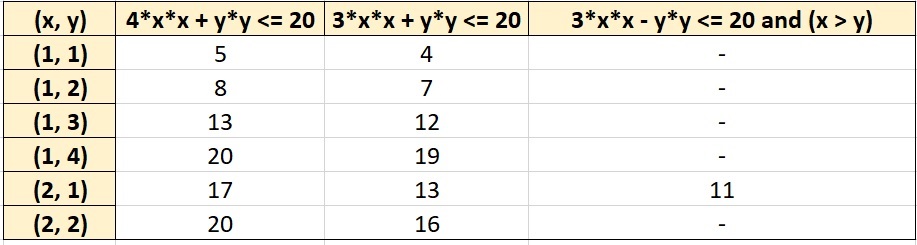
• Flipping the status according to condition.The above values of n in the table generated in x, y loop will be tested for modulo condition.
  * if (colum1 value) % 12 == 1 or 5:
  * then flip the sieve status for that number.
  *
  We are taking mod with 12 in place of 60, this is because if we take mod 60 then we have to consider many r as 1, 13, 17, 29, 37, 41, 49, or 53 and for all these r, mod 12 is 1 or 5. (done only to reduce the expression size).

status of 5, 13, 17 became true

• if (column 2 value) % 12 == 7
  • then flip the sieve status for that number.

status of 7, 19 becomes true

• if (column 3 value) % 12 == 11:
  • then flip the sieve status for that number.

status of 11 becomes true)</li>

• Checking for Square free Condition: If any number in our list in square of any number then remove it. // If square them make them non-prime and not added in the result.

• Creating array of prime numbers for which status is true and printing it as the output

2 3 5 7 11 13 17 19

Implementation

Following is the implementation of Sieve of Atkin in Python:

   def SieveOfAtkin(limit):
       #for 2 and 3
       if (limit > 2): 
           print(2 , end = " ") 
       if (limit > 3): 
           print(3 , end = " ")
       #intialize sieve
       sieve = [False] * limit 
       for i in range( 0 , limit ): 
           sieve[i] = False # here we are intializing each number as non-prime.
       #for step 3
       x = 1
       while(x * x < limit ) : 
           y = 1
           while(y * y < limit ) : 
           #main part
               n = (4 * x * x) + (y * y) 
               if (n <= limit and (n % 12 == 1 or 
                                n % 12 == 5)):
                    sieve[n] ^= True # changing status to prime.
               n = (3 * x * x) + (y * y) 
               if (n <= limit and n % 12 == 7): 
                   sieve[n] ^= True # changing status to prime.
               n = (3 * x * x) - (y * y) 
               if (x > y and n <= limit and 
                          n % 12 == 11): 
                   sieve[n] ^= True # changing status to prime.
               y += 1
            x += 1
            #mark all multiples of square as non-prime
            r = 5
            while(r * r < limit) : 
                if (sieve[r]) : 
                    for i in range(r * r, limit, r * r): 
                        sieve[i] = False # here we are changing status to non-prime and ignoring it.
           # Print primes 
           for a in range(5 , limit ): 
               if (sieve[a]): 
                   print(a , end = " ") 

limit = 20
SieveOfAtkin(limit)    

Applications

The Sieve of Atkin is a method considered as an optimized version of the Sieve of Eratosthenes to find all prime numbers up to a limit fixed N.

This algorithm can be used in the following cases:

• Determine whether a number N is a prime number or not.
• Factorize a number N.
• Find all prime numbers within a range N to M.
• Prove prime number theorems for a range like Goldbach’sConjecture.