Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes | Coding time: 5 minutes
A Union Find data structure(also called disjoint-set) is a data structure that keeps track of elements partitioned into a number of disjoint(non-overlapping) subsets.
It provides near-constant-time operations to add new sets, to merge existing sets, and to determine whether elements are in the same set.
Union Find data structure can be implemented by:
- Naive implementation
- Linked list
- Trees
1. Naive implementation
Here the idea is to use smallest element of the set as its ID. We Use array smallest[1...n]: where smallest[i] stores the smallest element in the set i belongs to.
* Pros:
1.Running time of Find is O(1).
2.well defined ID.
* Cons:
Running time of Union is O(n).
2. Using Linked list
Here the basic idea is to represent a set as a linked list, use the list tail as ID of the set.
* Pros:
1.Running time of Union is O(1).
2.Well-defined ID.
* Cons:
1.Running time of Find is O(n) as we need to traverse the list to find its tail.
2.Union(x,y) works in time O(1) only if we can get the tail of the list of x and the head of the list of y in constant time.
3. Using Trees
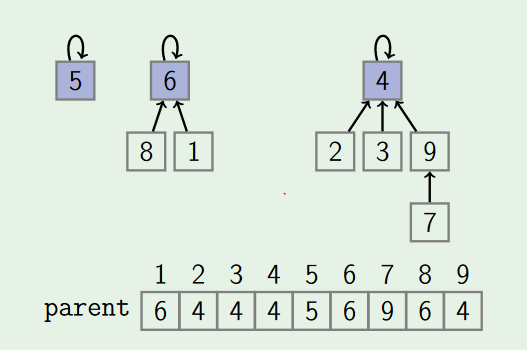
Here we represent each set as a rooted tree. ID of a set is the root of the tree. We use array parent[1...n]:where parent[i] is the parent of i, or i if it is the root.
* Pros:
1. Well defined ID.
2. Running Time of Find is O(log2n).
3. Running Time of Union is O(log2n).
where n is total elements.
Operations
A Union-Find data structure supports following operations:
- makeSet
- find
- by path compression
- Union
- by rank
- by size
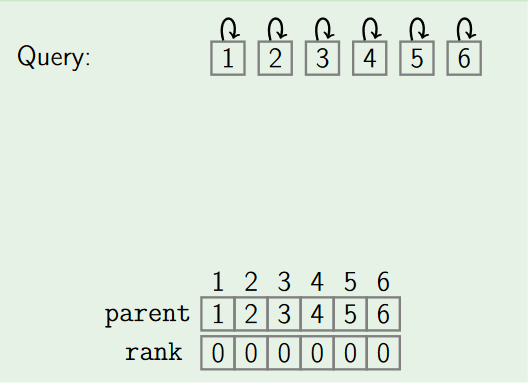
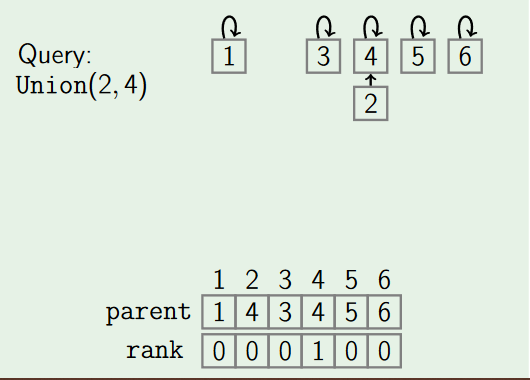
1. MakeSet
The MakeSet operation makes a new set by creating a new element with a unique id.So for n elements it creates n individual sets.
Pseudocode:
function MakeSet(x)
if x is not already present:
add x to the disjoint-set tree
x.parent := x
x.rank := 0
x.size := 1
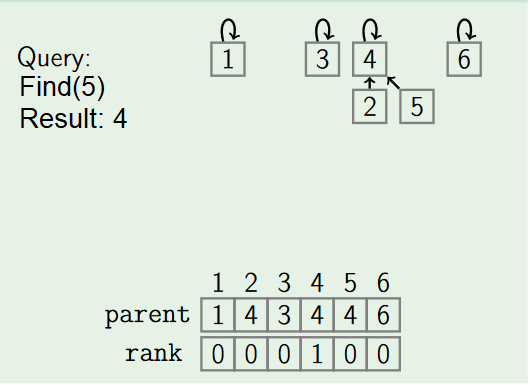
2. Find
Returns ID of set containing x:
* if x and y lie in the same set, then
Find(x) = Find(y)
* otherwise, Find(x) ≠ Find(y).
- by Path compression:
Path compression flattens the structure of the tree by making every node point to the root whenever Find is used on it. This is valid, since each element visited on the way to a root is part of the same set. The resulting flatter tree speeds up future operations not only on these elements, but also on those referencing them.
Pseudocode:
function Find(x)
if x.parent != x
x.parent := Find(x.parent)
return x.parent
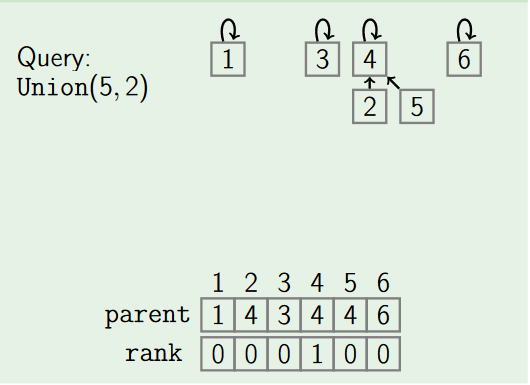
3. Union
The Union operation merges two sets containing x and y. After applying Union(x, y), both elements x and y becomes element of the same set.
- by Rank:
Union by rank always attaches the shorter tree to the root of the taller tree, thus the resulting tree is no taller than the original unless they were of equal height.
To implement this we assign rank to each element of set, initially the set have one element having rank zero. If two sets are unioned together and have different ranks then the resulting set's rank is larger of the two; otherwise, if two sets are unioned and have equal rank then the resulting set's rank will be one larger. Here we use rank instead of height because height of the tree will be changed by path compression over time.
Pseudocode:
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
// x and y are already in the same set
if xRoot == yRoot
return
// x and y are not in same set, so we merge them
if xRoot.rank < yRoot.rank
xRoot, yRoot := yRoot, xRoot // swap xRoot and yRoot
// merge yRoot into xRoot
yRoot.parent := xRoot
if xRoot.rank == yRoot.rank:
xRoot.rank := xRoot.rank + 1
- by Size:
Union by size always attaches the tree with fewer elements to the root of the tree with more elements.
Pseudocode:
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
// x and y are already in the same set
if xRoot == yRoot
return
// x and y are not in same set, so we merge them
if xRoot.size < yRoot.size
xRoot, yRoot := yRoot, xRoot // swap xRoot and yRoot
// merge yRoot into xRoot
yRoot.parent := xRoot
xRoot.size := xRoot.size + yRoot.size
Complexity
Time Complexity
Without path compression (or a variant), union by rank, or union by size, the height of trees can grows unchecked as O(n), implying that Find and Union operations will take O(n) time where n is total number of elements.
Using path compression alone gives a worst-case running time of Θ(n + f*(1 + log2+f/nn ) ) , for a sequence of n MakeSet operations (and hence at most n-1 Union operations) and f Find operations.
Using union by rank alone gives a running-time of O(log2n) (tight bound) per operation(for both Find and Union).
Using both path compression and union by rank or size ensures that the amortized time per operation is only O(log*n) (read as log star n which is inverse Ackermann function), which is optimized(for both Find and Union).
O(log*n) is much better than O(log n), as its value reaches at most up to 5 in the real world.
Space Complexity : O(2*n)
Implementations
Code in Python3
# python3
# Python Program for union-find algorithm to detect cycle in a undirected graph
import sys
from collections import defaultdict
# this function initializes all single element sets
def makeset(n):
parent = [None] * n
rank = [None] * n
for i in range(n):
parent[i] = i
rank[i] = 0
return parent, rank
# A function to find the ID of an element i
def find(parent, i):
if parent[i] != i:
# path compression
parent[i] = find(parent, parent[i])
return parent[i]
# A function to do union of two subsets by rank
def union(parent, rank, x, y):
xRoot = find(parent, x)
yRoot = find(parent, y)
# if both element in same sets
if xRoot == yRoot:
return
# both elements not in the same sets, merge them
# if rank of elements are different
if rank[xRoot] < rank[yRoot]:
# merge xRoot into yRoot
parent[xRoot] = yRoot
else:
# merge yRoot into xRoot
parent[yRoot] = xRoot
# if both elements have equal rank
if rank[xRoot] == rank[yRoot]:
rank[xRoot] += 1
# This class represents a undirected graph using adjacency list representation
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# The main function to check whether a given graph
# contains cycle or not
def isCyclic(self):
# Allocate memory for creating V subsets and
# Initialize all subsets as single element sets
parent, rank = makeset(self.V)
# Iterate through all edges of graph, find subset of both
# vertices of every edge, if both subsets are same, then
# there is cycle in graph.
for i in self.graph:
for j in self.graph[i]:
x = find(parent, i)
y = find(parent, j)
if x == y:
return True
union(parent, rank, x ,y)
input = sys.stdin.read()
data = list(map(int, input.split()))
vertices, edges = data[0:2]
data = data[2:]
g = Graph(vertices)
for i in range(edges):
u,v = data[0:2]
data = data[2:]
g.addEdge(u, v)
if g.isCyclic():
print "Graph contains cycle"
else :
print "Graph does not contain cycle "
Applications
- Union-Find is used to determine the connected components in a graph. We can determine whether 2 nodes are in the same connected component or not in the graph. We can also determine that by adding an edge between 2 nodes whether it leads to cycle in the graph or not.
We learned that we can reduce its complexity to a very optimum level, so in case of very large and dense graph, we can use this data structure.
- It is used to determine the cycles in the graph. In the Kruskal’s Algorithm, Union Find Data Structure is used as a subroutine to find the cycles in the graph, which helps in finding the minimum spanning tree.(Spanning tree is a subgraph in a graph which connects all the vertices, with minimum sum of weights of all edges in it is called minimum spanning tree).
References
- Wikipedia page on Union Find(Disjoint-Sets)
- Can see the chapters 21.1 and 21.2 in [CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms (3rd Edition). MIT Press and McGraw-Hill. 2009.