Longest Increasing Subsequence [3 techniques]

As the name suggest Longest Increasing Subsequence is to find the longest increasing subsequence in sequence such that elements of subsequence are in sorted increasing order.

Approcah to Solve this problem:
Longest Increasing Subsequence problem can be solved with the help of 3 different Approach:

1. Brute Force
2. Dynamic Programming
3. Binary Search

Time Complexity

Time Complexity of LIS:

1. Brute force: O(N^2)
2. Dynamic Programming: O(n^2)
3. Binary Search: O(nlogn)

Using Binary Search is a efficient Method
Reason: Possible increasing subsequences that can be formed with the elements seen so far, such that the sub-sequences we track are ones that could contribute to the final solution. We will aggressively discard subsequences that can never influence the solution, and this will allow the algorithm to become efficient.

NOTE: Longest Increasing Subsequence need not be consecutive in Original sequence

Example

array: 2,5,7,3,16,1,6,19
Subsequence 1: 2,5,7,16,19
Subsequence 2: 5,7,16,19
Subsequence 3: 2,3,6,19
Subsequence 4: 2,3,16,19
LIS: 2,5,7,16,19
(There can be many Subsequence, LIS has max. length)

Implementing LIS with Brute Force

Basic Idea:

The brute force solution is to consider all non-null subsets of Array. Then collect all the increasing subsequences and return the longest subsequence from them.

Pseudocode:

1. Import java.util.*
2. lis() returns the length of the longest increasing subsequence in arr[] of size n

     static int lis(int[] arr, int n)  
     int max = 0; 
     int[] lst = new int[n]; 
   

3. Initialize LIS values for all indexes

    Arrays.fill(lst, 1); 
   

4. Now, Compute optimized LIS values
   Create two for loop

   for (int i = 1; i < n; i++)  
      { 
          for (int j = 0; j < i; j++)  
          { 
          if (arr[i] > arr[j] &&  
          lst[i] < lst[j] + 1) 
          lst[i] = lst[j] + 1; 
          } 
      }
   

5.Pick maximum of all LIS values

for (int i = 0; i < n; i++) 
        if (max < lst[i]) 
            max = lst[i]; 
    return max; 

6.Write main function and provide input, and it will return the max. length of subsequence possible.

Implementation

Following is the implementation in Java programming language:

import java.util.*; 
class brute_LIS  
{ 
    static int lis(int[] arr, int n)  
    { 
        int max = 0; 
        int[] lst = new int[n]; 
  
        // initialize LIS values for all indexes 
        Arrays.fill(lst, 1); 
  
        // Compute optimized LIS values  
        for (int i = 1; i < n; i++)  
        { 
            for (int j = 0; j < i; j++)  
            { 
                if (arr[i] > arr[j] &&  
                    lst[i] < lst[j] + 1) 
                    lst[i] = lst[j] + 1; 
            } 
        } 
  
        //Pick maximum of all LIS values
        for (int i = 0; i < n; i++) 
            if (max < lst[i]) 
                max = lst[i]; 
  
        return max; 
    } 
  
    // Main function
    public static void main(String[] args)  
    { 
        int[] arr = { 10, 22, 9, 33, 21, 50, 41, 60 }; 
        int n = arr.length; 
        System.out.println("Length of lis is " +  
                                   lis(arr, n)); 
    } 
}

Output

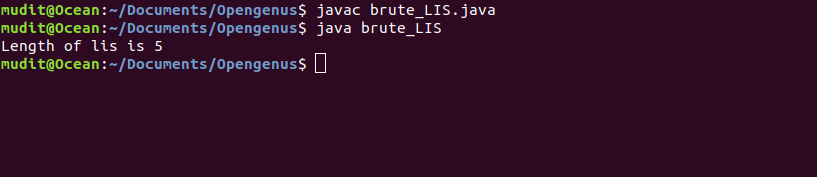
The Time Complexity of this approach using DP is O(N²).
The Space Complexity of this approach using DP is O(N).

Implementing LIS with Binary Search

Basic Idea:

Take original array and put elements of original arrays in increasing subsequence. While filling this subsequence, follow two rules:
Compare current and last if

• current > last: Append current element
• current <= last : Replace it with current element
  For Example:

Consider this Original Array, put 3 in increasing subsequence and then compare 3 with 1, Now 1 < 3, Apply 2 Rule: Replace it with current element i.e 1. Then 5, 5 > 1 , Append current element i.e 5. Now 2, 2 < 5, Replace it with 2. Now 6, 6 > 2, Append 6. Now 4 , 4 < 6. Replace 6 with 4
and Finally 9, 9 > 4 . Append 9.

Understand with this.
3
1<-5
1<-2<-6
1<-2<-4<-9

Pseudocode:

1. Create arrya for tracking the predecessors/parents of elements of each subsequence.

   int parent[] = new int[X.length];
   

2. Create a variable for tracking ends of each increasing subsequence.

   int increasingSub[] = new int[X.length + 1];
   

3. To calculate length of longest subsequence

   int length = 0;
   

4. Create for loop

   for(int i= 0; i<X.length; i++)
   

5. Implement Binary Search to calculate low,high and mid

   int low =1;
   int high = length;
   while(low <= high)
   {
   int mid = (int) Math.ceil((low + high)/2);
   if(X[increasingSub[mid]] < X[i])
      low = mid + 1;	
   else
      high = mid - 1;
   }
   int pos = low;
   

6. Conditions for LIS
   • Update parent/previous element for LIS or

   parent[i] = increasingSub[pos-1];
   

   • Replace or append

   increasingSub[pos] = i;
   

7. Now, update the length of the longest subsequence

   if(pos > length)
        length = pos;
   

8. Generate LIS by travering parent array
9. Create a main function and provide the input

Insights:

• Why replace if element of array is small?
  In the hope of getting a longer subsequence
• Why do we need to track parent?
  IncreasingSub array is not sufficient to remember multiple subsequences in consideration

Implementation

Following is the implementation in Java programming language:

public class LIS_binarySearch{
public static void LIS(int X[])
{
	int parent[] = new int[X.length];
//Track the predecessors/parents of elements of each subsequence.
	int increasingSub[] = new int[X.length + 1];
//Track ends of each increasing subsequence.
	int length = 0;
//Length of longest subsequence

for(int i= 0; i<X.length; i++)
{
	//Binary Search
	int low =1;
	int high = length;
	while(low <= high)
{
	int mid = (int) Math.ceil((low + high)/2);
	if(X[increasingSub[mid]] < X[i]){
	   low = mid + 1;
	}	
	else{
	   high = mid - 1;
	}
}

int pos = low;
//update parent/previous element for LIS
parent[i] = increasingSub[pos-1];
//Replace or append
increasingSub[pos] = i;

//update the length of the longest subsequence
if(pos > length)
	length = pos;
}

//Generate LIS by travering parent array
int LIS[] = new int[length];
int k = increasingSub[length];
for(int j = length-1;j>=0; j--)
{
	LIS[j] = X[k];
	k = parent[k];
}

for(int i = 0;i<length; i++)
{
	System.out.println(LIS[i]);
}
}

public static void main(String args[])
{
int X[] = {3,1,5,0,6,4,9};
LIS(X);
}
}

Output

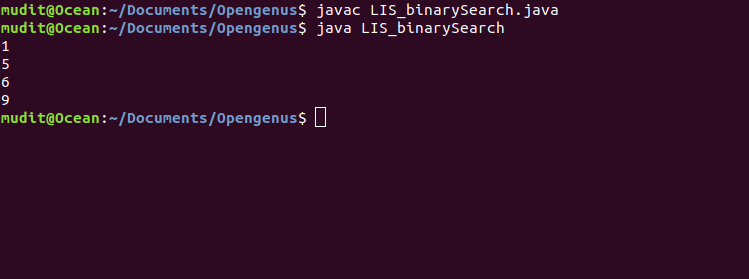
The Time Complexity of this approach using DP is O(N logN).
The Space Complexity of this approach using DP is O(N).

Implementing LIS with Dynamic Programming

Basic Idea:

Create 3 arrays: nums, sizes and paths
As the name suggest, nums is original array. sizes is to track the size of array and paths to track down the increasing subsequence array.
Initially, length is set to 1. Create two variable i and j . Now j is always at index 0 and i is at index 1. So, j always starts from 0 till j=i-1 and i is increment after j=i.
Here key is to compare j and i. So, if j < i then length is increment but max(j+1,previous len) is taken. Else ignore it and i is incremented.
And according mention and update path in third array.

Pseudocode:

1. Create a nums array that will store the sequence.
2. Now, create a size array to keep track of LIS ending with current position.

   int[] sizes = new int[nums.length]
   

3. And accordingly an array path to keep track of the path for printing out.

   String[] paths = new String[nums.length]
   

4. Now, check for every index if it is suitable for LIS.
5. Create two variable i,j
6. Base condition: Assign size of array equal to 1

   sizes[i] = 1
   paths[i] = nums[i]
   

7. Create a support varialbe called maxLenth to keep track.
8. Create two for loops:
   i will start at 1 index
   j will start at 0 index

   for(int i=1; i<nums.length; i++) 
     for(int j=0; j<nums.length; j++)
   

9. Condition:

   nums[j]<nums[i] and sizes[i] < sizes[j] + 1	
   if(maxLength < sizes[i])
   maxLength = sizes[i]
   

10.After checking condition i++ and j always starts from 0 index till i position.
11.Finally, LIS is printed.

Implementation

Following is the implementation in Java programming language:

public class LIS {
 public static void main(String[] args){

 int[] nums = {1,3,2,9,6,10,5};
 printLIS(nums);
 }

	//main function
	public static void printLIS(int[] nums){
	
	//creating size and path array
	String[] paths = new String[nums.length];
	int[] sizes = new int[nums.length];

//Initially, assign sizes and path position
for(int i=0; i<nums.length; i++){
	sizes[i] = 1;
	paths[i] = nums[i] + " " ;
}

//Creating maxLenth to keep track
int maxLength = 1; 

for(int i=1; i<nums.length; i++){ 
	for(int j=0; j<nums.length; j++){
// i at firstposition	
// j at zeroposition 

//here j<i and size must be increasing
if(nums[i]>nums[j] && sizes[i] < sizes[j] + 1){;
	//if so, we need to update sizes and path
	sizes[i] = sizes[j] + 1;
	paths[i] = paths[j] + nums[i] + " "; 
	// append current values to end!!
	
	if(maxLength < sizes[i])
		maxLength = sizes[i];
	}
   }
}

// finally go scanning the size of array again and print out the path when size matches
  for(int i=1; i<nums.length; i++){
    if(sizes[i] == maxLength)
	System.out.println("LIS: " + paths[i]);
  }
 }
}

Output

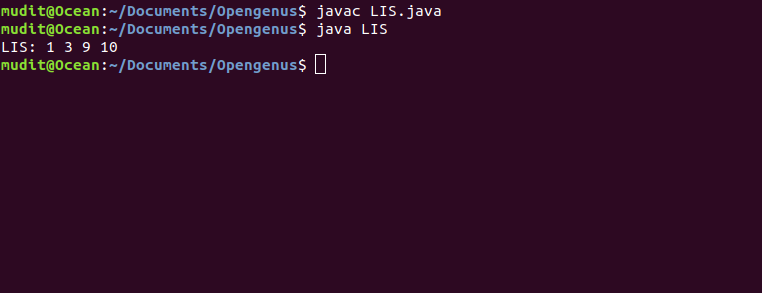
The Time Complexity of this approach using DP is O(N²).
The Space Complexity of this approach using DP is O(N).