Reverse a Queue using another Queue

In this article, we will explore how to reverse a Queue using another Queue.

Table of contents:

1. Introduction to Queue
2. Reverse Queue using Queue
3. Implementation
4. Time and Space Complexity analysis

Pre-requisite:

• Queue Data Structure
• Types of Queue and their implementations

Introduction to Queue

It is a linear structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO). It is an important data structure.

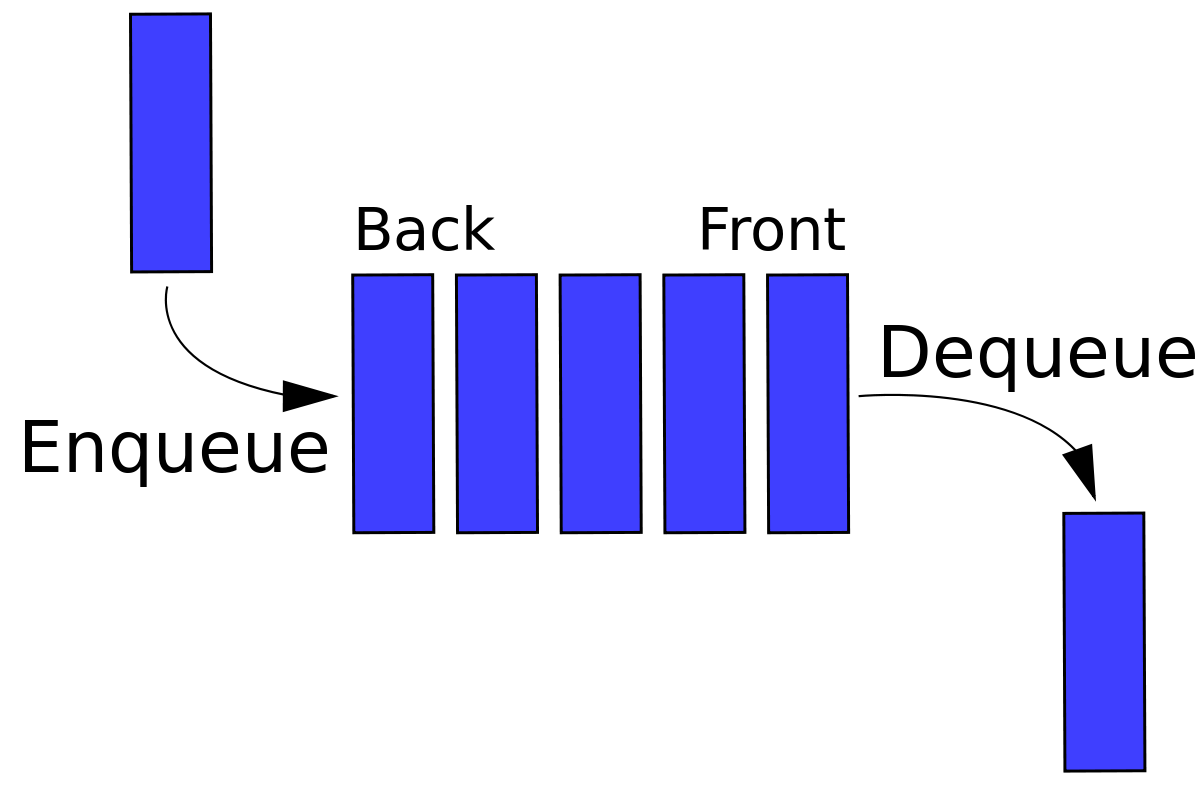
Example- Movie ticket counter queue, it is any queue of consumers for a resource where the consumer that came first is served first.
In the given picture below it simply explains a queue that the person coming first will leave the queue first.

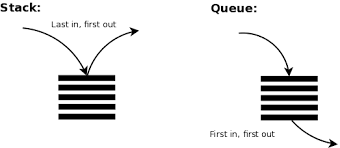
The difference between stacks and queues is in removing. In a stack we remove the item the most recently added that is the last item so it follows LIPO(last in first out); in a queue, we remove the item the least recently added that is the fisrt added item so it follows FIFO(first in first out).

Operations on Queue:

Enqueue: It adds an item to the queue. If the queue is full, then it is said to be in Overflow condition.
Dequeue: Removes an item from the queue. The items are removed out in the same order in which they are enqueued. If the queue is empty, then it is said to be in Underflow condition.
Front: it gives the front item from queue.
Rear: it gives the last item from queue.
Peek(): it gives the element at the front/peek of the container. This method will return the head of the queue. The method does not throws an exception when the Queue is empty, it returns null.

Reverse Queue using Queue

Hence this was our basic knowledge required to code the program "Reverse a queue using another queue".

Example:

Input:  queue[] = {1, 2, 3, 4, 5}
Output: 5 4 3 2 1

Input:  queue[] = {11, 12, 13, 14}
Output: 14 13 12 11

Approach:
We will take two queue q1 and q2. Suppose q1 contains {1,2,3,4,5} elements and we will reverse it and add it in q2 as {5,4,3,2,1}.

Algorithm:

1. Given two Queues q1 and q2.
2. Add the elements in the q1 and then iterate it over till size-2 of the q1 and add these elements at the rear end of q1, hence to get the last element at the first position.
3. Remove the first position element and add it to the q2.
4. Repeat these steps till the q1 is empty and q2 gets all the reversed elements.

Steps

1. q1 taken with {1,2,3,4,5} elements.
   [1, 2, 3, 4, 5]
2. peek element removed from front end, added to rear end.This will be done till q1.size()-2 = 4 times
   [2, 3, 4, 5, 1]
   [3, 4, 5, 1, 2]
   [4, 5, 1, 2, 3]
   [5, 1, 2, 3, 4]
3. Last element=5 removed from q1 and added to q2.
4. Again iterate till q1.size()-2=3 times as now one elemnt is removed and add it to rear end of queue.
   [2, 3, 4, 1]
   [3, 4, 1, 2]
   [4, 1, 2, 3]
5. Iterate till q1.size()-2=2 times as now two elemnt is removed and add it to rear end of queue.
   [2, 3, 1]
   [3, 1, 2]
6. Iterate till q1.size()-2=1 times as now three elemnt is removed and add it to rear end of queue.
   [2, 1]
7. Hence,only one element left, add it to the q2.
   [ 1 ]
8. Now the queue is reversed and added in q2.
   q2 - [5, 4, 3, 2, 1]

Implementation

Now let us code this algorithm.

package queue;

import java.util.LinkedList;
import java.util.Queue;

public class ReverseQueueUsingQueue {

	//reverse method
	public static void reverse(Queue<Integer> q1)
	{
		int n = q1.size();
		
		//queue 2 - q2
		Queue<Integer> q2 = new LinkedList<>();
		
		//iterate till all the last element are removed from q1 and added in q2 
		for(int i=0; i<n; i++)
		{
			//we have to iterate only till the 2nd last element so we will take the q1.size()-2 to get the last element at front of queue
			for(int j=0; j<q1.size()-1; j++)
			{
				//all elements till q1.size-2 are removed 
				int a = q1.remove();
				//After removal added at the rear end of queue 
				q1.add(a);
			}
			
			//last element of q1 added to q1
			q2.add(q1.peek());
			//last element of q1 removed  
			q1.remove();
		}
		
	//print all the elements
	 while(!q2.isEmpty())
	 {
		     System.out.print("Reversed queue - " + q2.peek() + " "); 
		     q2.remove(); 
	 }
    }
	
	public static void main(String[] args) {
		//queue 1 - q1 
		Queue<Integer> q1 = new LinkedList<>();
		
		q1.add(1);
		q1.add(2);
		q1.add(3);
		q1.add(4);
		q1.add(5);
		
		//static method called to reverse the elements
		reverse(q1);
		
	}

}

Output:

Reversed queue - 5 4 3 2 1

Time and Space Complexity analysis

In the algorithm, each element is processed twice. The first processing is when the elements are added to the end of the original queue and then, the second processing is when the elements are moved from first queue to second queue.

Assume there are N elements in the Queue, then there will be 2N steps. So, the Time Complexity of the algorithm will be linear that is O(N).

This can be considered to be theoretical optimal as we have to traverse through all elements in the queue to reverse it. This may not be true in specific cases like double ended queue. In case of Double ended queue, a programmer can consider the point of insert to be the point of deletion and vice versa. On this consideration, the cost of reversal becomes O(1).

In our particular case, we want to use a second queue so the proposed O(N) time algorithm is optimal.

As we are using a second queue to store the reversed queue, the Time Complexity of the algorithm is O(N). If we do not store the output (just print it) and we need not maintain the original state of the input data, then the space complexity of this algorithm can be reduced to O(1).

Hence, the Complexity of this algorithm is:

• Time Complexity: O(N)
• Space Complexity: O(N)

where there are N elements in the Queue.

With this article at OpenGenus, you must have the complete idea of reversing a Queue using Queue.